
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
І, навпаки, рівняння (5) при довільних коефіцієнтах А, В, С (А і В не дорівнюють нулю одночасно) визначає деяку пряму в прямокутній системі координат Оху
Теорема 1. У прямокутній системі координат Оху будь-яка пряма задається рівнянням першого степеня
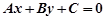 , (5)
, (5)
Лінії, що визначаються в прямокутній системі координат рівнянням першого степеня, називаються лініями першого порядку. Таким чином, кожна пряма є лінією першого порядку і, навпаки, кожна лінія першого порядку є пряма.
Рівняння виду Ах + Ву + С = 0 називається загальним, або пов ним, рівнянням прямої. При різних значеннях А, В, С воно визначає різні прямі.
Приклад. Пряму задано загальним рівнянням 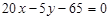 . Записати її рівняння з кутовим коефіцієнтом.
. Записати її рівняння з кутовим коефіцієнтом.
Ø Розв’язуючи загальне рівняння прямої відносно у, дістаємо рівняння з кутовим коефіцієнтом:
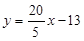 .
.
Тут 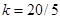 ,
, 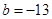 .
.
Дослідження загального рівняння прямої.
Рівняння прямої у відрізках
Розглянемо три частинні випадки, коли рівняння Ах + Ву + С = 0 неповне, тобто якийсь із його коефіцієнтів дорівнює нулю.
1. С = 0; рівняння має вигляд Ах + Ву = 0 і визначає пряму, що проходить через початок координат.
2. В = 0 (А ¹ 0); рівняння має вигляд Ах + С = 0 і визначає пряму, паралельну осі Оу. Згідно з теоремою 1 це рівняння зводиться до вигляду х = а, де а =С/А, а — величина відрізка, що його відтинає пряма на осі Ох (див. рис. 3). Зокрема, якщо а = 0, то пряма збігається з віссю Оу. Таким чином, рівняння x = 0 визначає вісь ординат.
3. А = 0 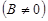 ; рівняння має вигляд Ву + С = 0 і визначає пряму, паралельну осі Ох. Це встановлюється аналогічно до попереднього випадку. Якщо взяти –С/B = b, то рівняння набирає вигляду
; рівняння має вигляд Ву + С = 0 і визначає пряму, паралельну осі Ох. Це встановлюється аналогічно до попереднього випадку. Якщо взяти –С/B = b, то рівняння набирає вигляду 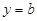 , де
, де 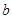 — величина відрізка, що відтинає пряма на осі Оу (рис. 4). Зокрема, якщо
— величина відрізка, що відтинає пряма на осі Оу (рис. 4). Зокрема, якщо 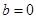 , то пряма збігається з віссю Ох. Таким чином, рівняння
, то пряма збігається з віссю Ох. Таким чином, рівняння 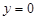 визначає вісь абсцис.
визначає вісь абсцис.
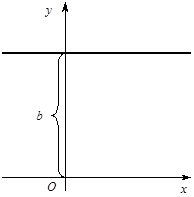
Рис. 4
Нехай тепер дано рівняння Ах + Ву + C = 0 за умови, що жодний із коефіцієнтів F, B, C не дорівнює нулю. Перетворимо його до вигляду
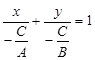 .
.
Позначивши 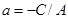 ,
, 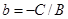 , дістанемо:
, дістанемо:
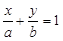 . (6)
. (6)
Рівняння (6) називається рівнянням прямою у відрізках. Числа а і b є величинами відрізків, що їх пряма відтинає на осях координат. Ця форма рівняння зручна для геометричної побудови прямої.
Приклад. Пряму задано рівнянням 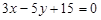 . Скласти її рівняння у відрізках і побудувати пряму.
. Скласти її рівняння у відрізках і побудувати пряму.
Ø Для даної прямої рівняння у відрізках має вигляд:
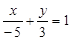 .
.

Рис. 31
Щоб побудувати цю пряму, відкладемо на осях координат Ох і Оу відрізки, величини яких відповідно дорівнюють а = –5, b = 3,
і проведемо пряму через точки 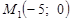 і
і 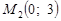 (рис. 5).
(рис. 5).
Кут між двома прямими
Розглянемо дві прямі L 1 і L 2. Нехай рівняння L 1 має вигляд 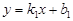 , де
, де 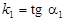 а рівняння L 2 — вигляд y = k 2 x + b, де
а рівняння L 2 — вигляд y = k 2 x + b, де 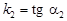 (рис. 6). Далі припустимо, що j — кут між прямими L 1 і L 2:
(рис. 6). Далі припустимо, що j — кут між прямими L 1 і L 2: 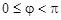 .
.
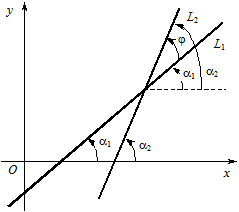
Рис. 6
З геометричних міркувань встановлюємо залежність між кутами  ,
, 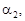
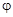 :
: 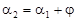 , або
, або 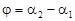 , звідки
, звідки
 ,
,
або
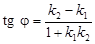 . (7)
. (7)
Формула (7) визначає один із кутів між прямими; інший кут дорівнює 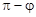 .
.
Приклад. Прямі задано рівняннями 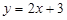 і
і 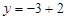 . Знайти кут між цими прямими.
. Знайти кут між цими прямими.
Ø Очевидно, 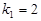 ,
, 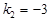 , тому відповідно до формули (7) знаходимо
, тому відповідно до формули (7) знаходимо
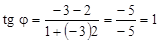 .
.
Таким чином, один із кутів між даними прямими дорівнює 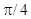 , інший кут
, інший кут 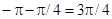 .
.
Умови паралельності і перпендикулярності
двох прямих
Якщо прямі L 1 і L 2 паралельні, то 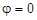 і tg j = 0. У цьому випадку чисельник правої частини формули (7) дорівнює нулю:
і tg j = 0. У цьому випадку чисельник правої частини формули (7) дорівнює нулю: 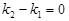 , звідки
, звідки
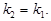
Таким чином, умовою паралельності двох прямих є рівність їхніх кутових коефіцієнтів.
Якщо прямі 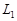 і
і 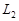 взаємно перпендикулярні, тобто
взаємно перпендикулярні, тобто 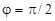 , то із (7) знаходимо
, то із (7) знаходимо
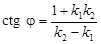 .
.
У цьому випадку 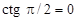 і
і 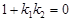 , звідки
, звідки

Таким чином, умова перпендикулярності двох прямих полягає в тому, що їхні кутові коефіцієнти взаємно обернені за величиною і протилежні за знаком.
Приклад. Показати, що прямі 4 х – 6 у + 7=0 і 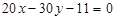 паралельні.
паралельні.
Ø Звівши рівняння кожної прямої до вигляду рівняння з кутовим коефіцієнтом (2), дістанемо:
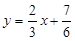 і
і 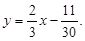
Кутові коефіцієнти цих прямих рівні між собою: 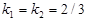 . Звідси випливає, що прямі паралельні.
. Звідси випливає, що прямі паралельні.
Приклад. Показати, що прямі 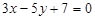 і
і 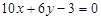 взаємно перпендикулярні.
взаємно перпендикулярні.
Ø Звівши рівняння до вигляду рівняння з кутовим коефіцієнтом (2), дістанемо:
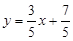 і
і 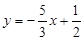 .
.
Тут 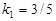 ,
, 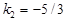 .
.
Оскільки 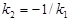 , то прямі взаємно перпендикулярні.
, то прямі взаємно перпендикулярні.
Відстань від точки до прямої
Теорема 2. Відстань d від даної точки M(x0; y0) до прямої L, заданої загальним рівнянням Ах + Ву + С = 0, визначається формулою:
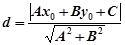 . (8)
. (8)
Приклад. Нехай пряму L задано рівнянням 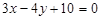 і дано точку
і дано точку 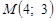 . Знайти відстань d від точки М до прямої L.
. Знайти відстань d від точки М до прямої L.
Ø За формулою (8) знаходимо
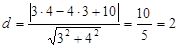 .
.
Таким чином, шукана відстань дорівнює 2.
Взаємне розташування двох прямих на площині
Нехай прямі L 1 і L 2 задано рівняннями:
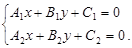 (9)
(9)
Розглянемо рівняння (9) як систему двох рівнянь першого степеня з двома невідомими х і у. Розв’язавши цю систему, знайдемо
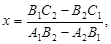
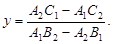
Нехай 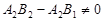 . Тоді записані формули дають розв’язок системи (9). Це означає, що прямі
. Тоді записані формули дають розв’язок системи (9). Це означає, що прямі 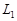 і
і 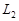 не паралельні і перетинаються в одній точці з координатами (х; у).
не паралельні і перетинаються в одній точці з координатами (х; у).
Нехай тепер 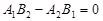 . Тоді можливі два випадки:
. Тоді можливі два випадки:
1) 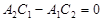 і
і 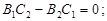
2) 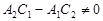
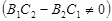 .
.
У першому випадку маємо 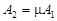 ,
, 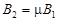 ,
, 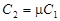 , або
, або
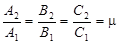 ,
,
де 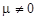 — деяке число. Це означає, що коефіцієнти рівнянь пропорційні, звідки випливає, що друге рівняння дістаємо з першого множенням на число m. У цьому випадку прямі L 1 і L 2 збігаються, тобто рівняння визначають ту саму пряму. Очевидно, система (9) має нескінченну множину розв’язків.
— деяке число. Це означає, що коефіцієнти рівнянь пропорційні, звідки випливає, що друге рівняння дістаємо з першого множенням на число m. У цьому випадку прямі L 1 і L 2 збігаються, тобто рівняння визначають ту саму пряму. Очевидно, система (9) має нескінченну множину розв’язків.
У другому випадку припустимо, наприклад, 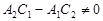 . Тоді, припустивши, що система має розв’язок (х 0; у 0), прийдемо до суперечності. Справді, підставляючи в рівняння замість х і у значення
. Тоді, припустивши, що система має розв’язок (х 0; у 0), прийдемо до суперечності. Справді, підставляючи в рівняння замість х і у значення 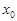 і
і 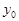 , множачи перше рівняння на А 2, друге — на
, множачи перше рівняння на А 2, друге — на 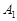 і віднімаючи від першого результату другий, дістаємо
і віднімаючи від першого результату другий, дістаємо 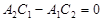 , що суперечить припущенню. Таким чином, система (9) не має розв’язку. У цьому випадку прямі
, що суперечить припущенню. Таким чином, система (9) не має розв’язку. У цьому випадку прямі 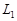 і
і 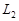 не мають точок перетину, тобто вони паралельні.
не мають точок перетину, тобто вони паралельні.
Отже, дві прямі на площині або перетинаються в одній точці, або збігаються, або паралельні.
1. Скласти рівняння прямої, що відтинає на осі Оу відрізок 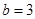 і утворює з віссю Ох кут: а) 45°, б) 135°. Побудувати цю пряму.
і утворює з віссю Ох кут: а) 45°, б) 135°. Побудувати цю пряму.
Відповідь. а) у = х + 3; б) у = – х + 3.
2. Визначити параметри k і b для кожної з прямих:
а) 2 х – 3 у = 6; б) 2 х + 3 у = 0; в) у = – 3; г) х /4 – у /4 = 1.
Відповідь. а) 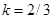 ;
; 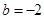 ; б)
; б) 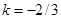 ;
; 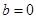 ; в)
; в) 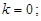
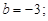 г)
г) 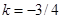 ;
; 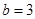 .
.
3. Визначити параметри k і b прямої, що проходить через точку А (2; 3) і утворює з віссю Ох кут 45°. Скласти рівняння цієї прямої.
Відповідь. 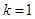 ,
, 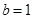 ,
, 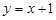 .
.
4. Звести до вигляду рівнянь у відрізках на осях рівняння прямих: а) 2 х – 3 у = 6; б) 3 х – 2 у + 4 = 0.
Відповідь. а) х/3 – у/2 = 1; б) 3х – 2у + 4 = 0.
5. Скласти рівняння прямої, що проходить через точки А (–1; 3) і В (4; –2).
Відповідь. 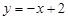 .
.
6. Скласти рівняння прямих, заданих параметрами: а) 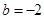 ,
, 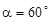 ; б)
; б) 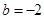 ,
, 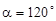 . Побудувати ці прямі.
. Побудувати ці прямі.
Відповідь. а) 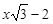 ; б)
; б) 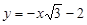 .
.
7. Визначити точки перетину прямої 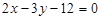 з осями координат і побудувати цю пряму.
з осями координат і побудувати цю пряму.
Відповідь. (6; 0), (0; –4).
8. Знайти точку перетину прямих 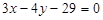 і
і 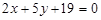 .
.
Відповідь. (3; –5).
9. Сторони АВ, ВС і АС трикутника АВС задано відповідно рівняннями 4 х + 3 у – 5 = 0, х – 3 у + 10 = 0, х – 2 = 0. Визначити координати його вершин.
Відповідь. А (2; –1), В (–1; 3), С (2; 4).
10. Скласти рівняння двох прямих, що проходять через точку А (4; 5), так, щоб одна була паралельна осі Ох, а інша — осі Оу.
Відповідь. у = 5, х = 4.
11. Визначте кут між прямими:
а) 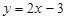 і
і 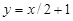 ; б)
; б) 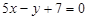 і
і 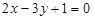 ;
;
в)  і
і 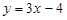 ; г)
; г) 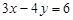 і
і 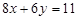 .
.
Відповідь. a) arctg 3/4; б) 45°; в) 45°; г) 90°.
12. Скласти рівняння прямих, що проходять через точку А (–1; 1) під кутом 45° до прямої 2 х + 3 у = 6.
Відповідь. 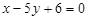 і
і 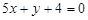 .
.
13. Скласти рівняння перпендикуляра, опущеного з точки А (6; 2) на пряму 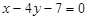 .
.
Відповідь.  .
.
14. Скласти рівняння прямої, що проходить через точку
А (–4; 3) і паралельна прямій 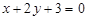 .
.
Відповідь. 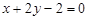 .
.
15. Скласти рівняння прямої, що проходить через точку перетину прямих 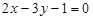 і
і 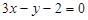 перпендикулярно до прямої
перпендикулярно до прямої 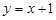 .
.
Відповідь. 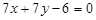 .
.
16. Дано трикутник із вершинами А (–2; 0), В (2; 4) і С (4; 0). Скласти рівняння сторін трикутника, медіани АЕ і висоти AD. Знайти довжину медіани АЕ.
Відповідь. АЕ: 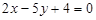 ;
;
AD: 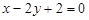 ;
; 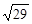 .
.
17. Знайти відстані точок А (4; 3), В (2; 1), С (1; 0) і О (0; 0) від прямої
 .
.
Побудувати точки і пряму.
Відповідь. 2,8;0; 1,4; 2.
18. Довести, що прямі 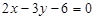 і
і 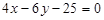 паралельні, і знайти відстань між ними.
паралельні, і знайти відстань між ними.
Відповідь. 6,5.
Вказівка. На одній із прямих взяти довільну точку і знайти її відстань від іншої прямої.
19. Знайти k з умови, що пряма y = kx + 5 віддалена від початку координат на відстань 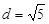 .
.
Відповідь.k = ±2.
20. Скласти рівняння прямої, що проходить через точку А (2; 4) і віддалена від початку координат на відстань 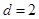 .
.
Відповідь. 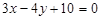 ;
; 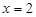 .
.
21. Через початок координат проведено пряму на однаковій відстані від точок А (2; 2) і В (4; 0). Знайти цю відстань.
Відповідь. Рівняння прямих:  і
і 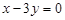 ; відстані:
; відстані: 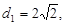
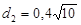 .
.
22. Скласти рівняння прямої, що проходить через точку перетину прямих 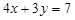 і
і 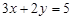 і утворює з віссю Ох той самий кут, що й пряма
і утворює з віссю Ох той самий кут, що й пряма 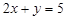 .
.
Відповідь. 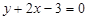 .
.
23. Даний трикутник з вершинами А (2; 3), В (4; 8) і С (3; –8). Складіть рівняння його сторін, медіан і висот.
Відповідь. АВ: 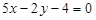 ;
;
АС: 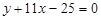 ;
;
ВС: 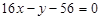 .
.
Рівняння медіан:
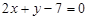 ;
; 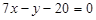 ;
; 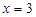 .
.
Рівняння висот:
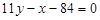 ;
;  ;
; 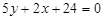 .
.

1. Що називається кутом нахилу прямої до осі Ох?
2. Що називається кутовим коефіцієнтом прямої?
3. Виведіть рівняння прямої з кутовим коефіцієнтом.
4. У чому полягає геометричний зміст параметрів k і b рівняння прямої з кутовим коефіцієнтом?
5. Вивести рівняння прямої, що проходить через задану точку і має даний кутовий коефіцієнт.
6. Вивести рівняння прямої, що проходить через дві дані точки.
7. Що називається загальним рівнянням прямої?
8. Довести, що рівняння прямої завжди є рівнянням першого степеня і, навпаки, усяке рівняння першого степеня є рівнянням прямої.
9. Дослідіть загальне рівняння прямої 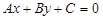 при
при 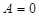 , при
, при 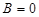 і при
і при 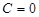 .
.
10. Як записуються рівняння прямих, паралельних осям Ох і Оу, а також рівняння самих осей координат?
11. Як перетворити загальне рівняння прямої в рівняння з кутовим коефіцієнтом?
12. Вивести формулу, якою подається кута між двома прямими.
13. Сформулювати умови паралельності і перпендикулярності двох прямих.
14. Як визначається відстань від точки до прямої?
15. Як знайти точку перетину двох прямих?
16. В яких випадках дві прямі на площині або збігаються, або паралельні?
1. Зобразити на координатній площині наведені далі точки:
(6; 2), (12; 1), (9; 2), (12; 0), (11; 2), (9; –2), (4; –2), (2; –1), (1; 1),
(–1; 1), (–2; 0), (–2; –2), (2; 1), (5; 2), (12; 2); (9; 1), (10; –2), (10; 0), (4; 1), (2; 2), (–2; 2), (–2; 1), (–2; –1), (0; 0); (2; 0), (2; –2), (4; 0),
(4; –1), (12; –1), (12; –2), (11; 0), (7; 2), (9; 0), (4; 2).
2. Не будуючи точку А (1; –3), з’ясуєте, в якій чверті вона міститься.
3. В яких чвертях може міститися точка, якщо її абсциса додатна?
4. На осі Ох узято точку з координатою (–5). Які її координати на площині?
5. Точки А (3; 2) і В (а; –1) містяться на прямій, паралельній осі Оу. Знайти значення а.
6. Точка М є серединою відрізка ОА, що сполучає початок координат О із точкою А (–5; 2). Знайти координати точки М.
7. Дано точки 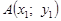 і
і 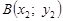 . Довести, що формула відстані між точками А і В не залежить від знаків їхніх координат.
. Довести, що формула відстані між точками А і В не залежить від знаків їхніх координат.
8. а) Яка точка —  чи
чи 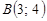 — далі від осі Ох?
— далі від осі Ох?
б) Яка з цих точок далі від осі Оу?
в) Чому дорівнює відстань від точки 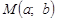 до осі Ох; осі Оу?
до осі Ох; осі Оу?
9. Побудувати точки А (4; 1), В (3; 5), С (–1; 4) і D (0; 0). Якщо точки побудовано правильно, то, сполучивши їх, дістанемо квадрат. Яка його площа? Чому дорівнює довжина сторони цього квадрата? Знайти координати середин сторін квадрата.
10. Знайти координати центра мас однорідної пластинки, що має форму трикутника з вершинами А (2; 4), В (0; 1); С (4; –2) (рис. 1).
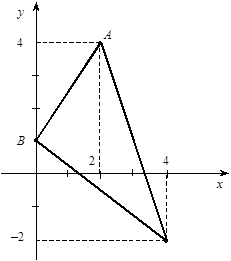
Рис. 1
11. Точки А (–2; 1), В (2; 3) і С (4; –1) — середини сторін трикутника. Знайти координати його вершин.
12. На площині дано точки А (0; 0), 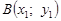 і
і 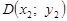 (рис. 2). Які координати повинна мати точка С, щоб чотирикутник ABCD був паралелограмом?
(рис. 2). Які координати повинна мати точка С, щоб чотирикутник ABCD був паралелограмом?
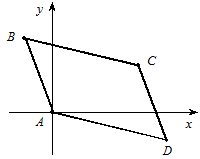
Рис. 2
13. Площа трикутника дорівнює 10 кв. од., дві його вершини — точки А (5; 1) і В(–2; 2). Знайти координати третьої вершини, коли відомо, що вона лежить на осі абсцис.
14. Знайти площу чотирикутника з вершинами в точках А (3; 1), В (4; 6), С (6; 3) і D (5; –2).
15. Дано полярні координати точки: 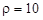 ,
, 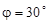 . Знайти її прямокутні координати, коли відомо, що полюс міститься в точці (2; 3), а полярна вісь паралельна осі абсцис.
. Знайти її прямокутні координати, коли відомо, що полюс міститься в точці (2; 3), а полярна вісь паралельна осі абсцис.
16. Знайти відстань між точками, знаючи їхні полярні координати: 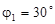 ,
, 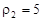 ,
,  .
.
17. Знайти множини точок, координати яких пов’язані такими співвідношеннями:
1) 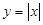 ; 2)
; 2) 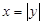 ; 3)
; 3) 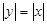 ; 4)
; 4) 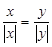 ; 5)
; 5) 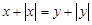 ; 6)
; 6) 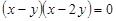 ; 7)
; 7) 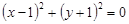 ; 8)
; 8) 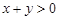 ; 9)
; 9) 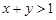 ; 10)
; 10) 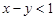 ; 11)
; 11) 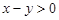 ,
, 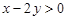 ; 12)
; 12) 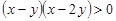 .
.
18. Скласти рівняння, що описують такі множини точок:
а) пряму, паралельну осі абсцис, що проходить через точку (1; 0); б) пряму, паралельну прямій 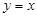 , що проходить через точку
, що проходить через точку
(–3; 7); в) множину точок, що містяться на відстані 2 від осі Оу.
19. Яким має бути співвідношення між х і у, щоб на координатній площині було задано: а) пару прямих у = 3 х і у = х – 3,
б) пряму у = х і точку (–1; 2); в) частину площини, що лежить вище від прямої у = х (включаючи цю пряму); г) частину площини між прямими у = 0 і у = 1 (без цих прямих); д) внутрішню область квадрата з вершинами в точках (0; 0), (0; 1), (1; 1), (1; 0).
20. На площині дано три точки: А (3; –6), В (–200; 400), С (1000; –2000). Довести, що вони лежать на одній прямій.
21. Які три з точок А (1; 3); B (–2; l); C (–l; 7), D (3; l) лежать на одній прямій?
22. Застосувати формулу відстані між двома точками на координатній площині для доведення такої теореми: у паралелограмі сума квадратів довжин діагоналей дорівнює сумі квадратів довжин його сторін.
23. Встановити:
а) чи лежить точка N (4,1; 1,9) на колі з центром C (1; –2) і радіусом 5 (скористайтеся рис. 3);
б) чи лежить точка K (0; 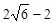 ) на цьому самому колі;
) на цьому самому колі;
в) чи лежить точка F (160; –1) на колі з центром (147; –6) і радіусом 13.
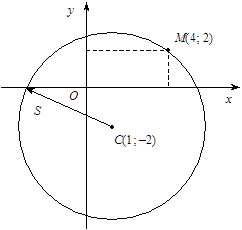
Рис. 3
24. Скласти рівняння кола з центром C (–2; 3) і радіусом, що дорівнює 5. Відомо, що точка A (а; –1) лежить на цьому колі. Знайти а.
25. Скласти рівняння кожної з чотирьох прямих, зображених на рис. 4.
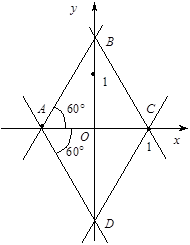
Рис. 76
26. Скласти рівняння прямої, яка паралельна бісектрисі першого координатного кута і проходить через точку (0; –5).
27. Скласти рівняння прямої, яка паралельна прямій 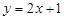 і проходить:
і проходить:
а) через точку (0; 2);
б) через точку (1; –1).
28. Дано пряму 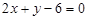 і на ній дві точки А і В з ординатами
і на ній дві точки А і В з ординатами 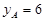 і
і 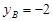 . Скласти рівняння висоти AD трикутника АОВ, і знайти її довжину, а також площу трикутника АОВ.
. Скласти рівняння висоти AD трикутника АОВ, і знайти її довжину, а також площу трикутника АОВ.
29. Скласти рівняння прямої, що проходить через точку
(–1; 1) так, що середина її відрізка, уміщеного між прямими 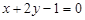 і
і 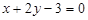 , лежить на прямій
, лежить на прямій 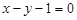 .
.
30. Знайти рівняння бісектрис кутів, утворених прямими 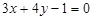 і
і  .
.
|
|
Дата добавления: 2014-01-04; Просмотров: 6023; Нарушение авторских прав?; Мы поможем в написании вашей работы!