Розщеплення енергетичних рівнів атомів в магнітному полі

Квантова електроніка вивчає методи посилення й генерації електромагнітних коливань з використанням вимушеного випромінювання квантових систем. Досягнення в цій галузі знань знаходять все більше застосування в медицині. Ознайомимося з деякими явищами, лежащими в основі квантової електроніки.

Такий пристрій, як лазер, і такі явища, як магнітний резонанс, стали активно застосовуватися в медицині в останнім часом.

У цій лекції як і в попередній, розглядаються явища, пов'язані в основному з випромінюванням і поглинанням енергії атомами і молекулами.

§ 16.1. ЛАЗЕРИ (ОКГ) ТА ЇХ ЗАСТОСУВАННЯ У МЕДИЦИНІ

Незважаючи на загальну природу світлових і радіохвиль, багато років оптика та радіоелектроніка розвивалися самостійно, незалежно один від одного. Здавалося, що джерела світла - порушені частинки і генератори радіохвиль - мають мало спільного. Лише з середини нашого століття з'явилися роботи по створенню молекулярних підсилювачів і генераторів радіохвиль, які поклали початок нової самостійної галузі фізики - квантової електроніці.

При вимушеній (індукованих) випромінюванні кількість переходів, що були скоєні в секунду, залежить від числа фотонів, що потрапляють в речовина за цей же час, тобто від інтенсивності світла. Крім того, вимушені переходи будуть визначатися заповнення, або, як кажуть, населенню (заселеності) відповідних збуджених енергетичних станів.

Індукованих випромінювання тотожно падає в усіх відношеннях, в тому числі і по фазі, тому можна говорити про когерентного посилення електромагнітної хвилі.

Для окремої частинки рівно імовірне вимушене поглинання, якщо частка знаходиться в основному стані, і випромінювання, якщо частка порушено.

Тому навіть якщо число збуджених частинок в речовині дорівнює числу не збуджених, посилення падаючою електромагнітної хвилі не буде. На справді в звичайному стані речовини число не збуджених частинок більше, ніж на будь-якому збудженому рівні. Таким чином, умови для посилення хвилі ще гірше.

Розподіл часток з енергетичних рівнів описується законом Больцмана, який графічно спільно з енергетичними рівнями показано на рис. 16.1. На малюнку «довжина» кожного рівня пропорційна числу часток, що мають відповідну енергію.

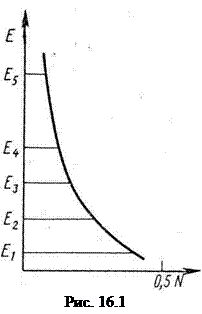Посилення електромагнітних хвиль можна викликати, використовуючи активну середовище, в якому хоча б для двох рівнів було розподіл часток, зворотне больцмановскому (інверсне населеність).

Цей стан формально виходить з розподілу Больцмана для Т <0К, тому називається станом з негативною температурою. У міру поширення світла в такому середовищі інтенсивність його зростає, має місце явище, зворотне поглинання. Це означає, що в законі Бугера I _e= I ₀ e ^-kl, k <0, тому інверсній населеності відповідає середовищі з негативним показником поглинання.

Стан з інверсного населення можна створити, відбираючи відповідні частки або спеціально збуджений частинки, наприклад, світлом або електричним розрядом. Само по собі стан з негативною температурою довго не існує.

Явище вимушеного випромінювання використовують у квантових генераторах (підсилювач). Перший такий генератор в діапазоні НВЧ, (мазер) був збудований у 1955р. незалежно радянськими вченими Н. Г. Басовий та О. М. Прохорова та американськими - Ч. Таунсом і др.1 Так як робота цього приладу була заснована на вимушеній випромінюванні молекул аміаку, то генератор був названий молекулярним.

У 1960р. був створений перший квантовий генератор видимого діапазону випромінювання - лазер ² з рубінами в якості робочого речовини. Цей оптичний квантовий генератор (ОКГ) створює імпульсне випромінювання з довжиною хвилі 694,3нм і потужністю в імпульсі 1 МВт. Збудження, або, за термінологією квантової електроніки, накачування здійснюється спеціальною лампою.

У тому ж році був створений газовий гелій-неоновим лазер, збудження в якому виникало при електричному розряді. Випромінюючих є атоми неон, атоми гелію відіграють допоміжну роль. На рис. 16.2 показані енергетичні рівні атомів гелію і неон. При електричному розряді частина атомів неон переходить з основного рівня 1 на порушення 3. Для чистого неон час життя на цьому рівні мало і атоми переходять на рівні 1 або 2, реалізується больцмановський розподіл. Для створення інверсної населеності потрібно якимось чином збільшити населеності рівня 3 та зменшити на рівні 2.

Атоми гелію сприяють збільшенню населеності рівня 3. Перший порушених рівень гелію збігається з рівнем 3 неон, тому при ударі порушеного атома гелію з не збуджених атомом неон відбувається передача енергії.

Для розвантаження рівня 2 підбирають такий розмір газорозрядні трубки, щоб при ударі з її стінками атом неон віддавав енергію, переходячи з рівня 2 на 1. Так забезпечується стаціонарність інверсної населеності рівнів 2 і 3 неон.

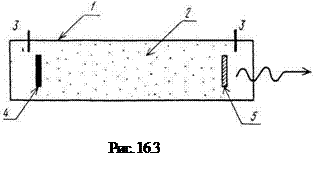
Основним конструктивним елементом гелій-неонового лазера (рис. 16.3) є газорозрядна трубка 1, звичайно кварцова, діаметром близько 7мм. У трубці 2 при тиску близько 150Па знаходиться суміш гелію і неон (гелію приблизно в 10 разів більше, ніж неон). В трубку вмонтовані електроди 3 для створення газового розряду. На кінцях трубки розташовані плоско-паралельні дзеркала 4 і 5, одне з них (5) напівпрозоре. Фотонів, що виникають при вимушеній випромінюванні, в залежності від напрямку їх руху або вилітають з бічній поверхні трубки, або, багаторазово відображаючи від дзеркал, самі викликають вимушені переходи. Таким чином, пучок, перпендикулярні дзеркалах, матиме найбільшу розвиток і виходить назовні через напівпрозоре дзеркало 5.

Це лазер безперервної дії. Так як рівні 2 і 3 неон володіють складною структурою (на рис. 16.2 не показані), то гелій-неоновим лазер може працювати на 30 довжин хвиль в області видимого і інфрачервоного діапазонів. Дзеркала 4 і 5 роблять з багатошаровими покриттями, і внаслідок інтерференції створюється необхідний коефіцієнт відображення для заданої довжини хвилі. Так, червоним гелій-неоновим лазером випромінюється довжина хвилі 632,8нм.

Застосування лазерів засноване на властивостях їх випромінювання: сувора монохроматичність (Δλ≈0,01нм), досить велика потужність, вузький пучок і когерентність.

Лазери використовують для вимірювання відстані між Землею і Місяцем (одержувана точність - близько десятків сантиметрів), для голографії, для пропалювання малих отворів, як засіб зв'язку і т.д.

Лазер знаходить програму і в медицині. Можна вказати два основних напрямки.

Перше, засноване на властивості лазерів руйнувати біологічні тканини, що спільно з коагуляції білка дозволяє виробляти деякі безкровно розсічення. У цьому напрямку можна відзначити наступні застосування: безопераційного лікування відшарування, сітківки, для цієї мети створений спеціальний лазерний прилад - офтальмокоагулятор; світловий безкровний ніж в хірургії, який не потребує стерилізації; лікування глаукоми за допомогою «проколювання» лазером отворів розміром 50-100мкм для відтоку внутрішньоочної рідини; знищення ракових клітин; руйнування дентину при лікуванні зубів.

Друге, напрямок пов'язано з голографії (див..). Так, наприклад, на основі гелій-неонового лазера з використанням волоконної оптики розроблені гастроскопи, які дозволяють голографічних формувати об'ємне зображення внутрішньої порожнини шлунка.

Гелій-неоновим лазер знаходить застосування для лікування ряду захворювань (трофічні виразки, ішемічна хвороба серця та ін.)

В лекції було показано, що на контур з струмом, поміщений в магнітне поле, діє момент сили. При стійкому рівновазі контуру його магнітний момент збігається з напрямком вектора магнітної індукції. Таке положення займає контур з струмом, наданий самому собі. Істотно інакше орієнтуються в магнітному полі магнітні моменти частинок. Розглянемо це питання з позиції квантової механіки.

Раніше зазначалося, що проекція моменту імпульсу електрона на деякий напрямок приймає дискретні значення. Щоб виявити ці проекції, необхідно якимось чином виділити напрямок Z. Один з найбільш поширених способів - завдання магнітного поля, в цьому випадку визначають проекцію орбітального моменту імпульсу 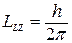m_e, проекцію спіна 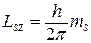, проекцію повного моменту імпульсу електрона 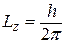m_j і проекцію моменту імпульсу атома 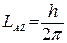m_J, на направлення вектора магнітної індукції В.

Зв'язок між моментом імпульсу і магнітним моментом дозволяє використовувати перераховані формули для знаходження дискретних проекцій відповідного магнітного моменту на напрямок вектора В. Таким чином, на відміну від класичних уявлень магнітні моменти частинок орієнтуються щодо магнітного поля під деякими певними кутами.

Для атома, наприклад, із 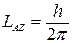m_j отримуємо наступне значення проекцій магнітного моменту на направлення вектора магнітної індукції:

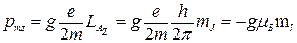(16.1.1)

де μ _Б =eh/(4πm) — магнетон Бора; g — множник Ланде (g-фактор), для заданого рівня енергії атома він залежить від квантових чисел L, J, S. Знак «—» в (16.1) зумовлений негативним зарядом електрона.

Формулу Е_П=р_mBcosα для енергії контуру з струмом в магнітному полі можна застосувати і до атому. З огляду на те, що р_mcosα дорівнює проекції р_mz магнітного моменту на напрямок вектора магнітної індукції, отримуємо

Е_П= - р_mBcosα= - р_mzB= gμ _Б Bm_J.

Таким чином, енергія атома в магнітному полі з урахуванням, що при його відсутності енергія атома дорівнює E₀, визначається за формулою

Е=Е₀+gμ _Б Bm_J, (16.1.2)

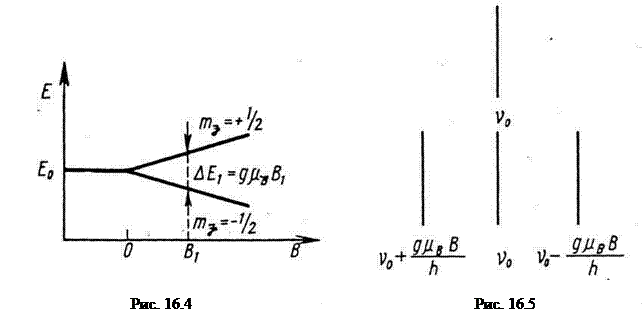
Так як магнітне квантової число m_J може приймати 2 J +1 значень від + J до - J, то з (16.2) випливає, що кожен енергетичний рівень при приміщенні атома в магнітне поле розщеплюється на 2 J +1 підрівнів. Це схематично показано на рис. 16.16. для J =1/2. Відстань між сусідніми підрівнів дорівнює

ΔЕ=gμ _Б B. (16.1.3)

Розщеплення енергетичних рівнів призводить і до розщепленню спектральних ліній атомів, поміщених в магнітне поле. Це явище називають ефектом Зеемана.

Запишемо вираз (16.2) для двох підрівнів Е₁ и Е₂, утворених при накладенні магнітного поля:

Е₁=E₀₁+gμ _Б Bm_J, Е₂=E₀₂+gμ _Б Bm_J, (16.1.4)

де E₀₁ и E₀₂ — енергії атома при відсутності магнітного поля. Використовуючи hυ=E_i-E_k и (16.4), отримуємо вираз для випромінюваних атомом частот:

υ=(E₀₂-E₀₁)/h+μ _Б B(g₂m_J2-g₁m_J1)/h=υ₀+Δυ, (16.1.5)

де

υ₀=(E₀₂-E₀₁)/h (16.1.6)

— частота спектральної лінії при відсутності магнітного поля:

Δυ = μ _Б B(g₂m_J2-g₁m_J1)/h (16.1.7)

— розщеплення спектральної лінії в магнітному полі. З (16.7) видно, що Δυ залежить від магнітного квантового числа, множник Ланде та магнітної індукції поля. Якщо g₁=g₂=g, то

Δυ = gμ _Б B(m_J2-m_J1)/h.

Згідно з правилами відбору для магнітного квантового числа, маємо

Δm_J=m_J2-m_J1=0, ±1. (16.1.8)

Це відповідає трьом можливим частотам: υ₀+gμ _Б B/h, υ_{0 ,} υ₀+gμ _Б B/h, тобто в магнітному полі спектральна лінія розщеплюється на триплети (рис. 16.5). Таке розщеплення називається нормальним або простим ефектом Зеемана; він спостерігається тільки в сильних магнітних полях.

У слабких магнітних полях існує аномальний ефект Зеемана, у цьому випадку g₁≠g₂ і розщеплення спектральних ліній значно більш складна.

Дата добавления: 2014-01-04