Функція Гріна граничних задач оператора теплопровідності

Лекція 19

Будемо розглядати граничні задачі для рівняння теплопровідності:

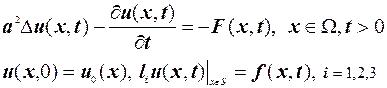(3.19)

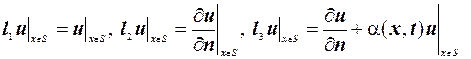- оператори граничних умов першого, другого, або третього роду.

Означення 3 Функцію 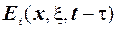будемо називати функцією Гріна першої, другої або третьої граничної задачі рівняння теплопровідності в області 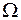с границею 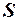і 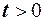, якщо вона є розв’язком наступної граничної задачі

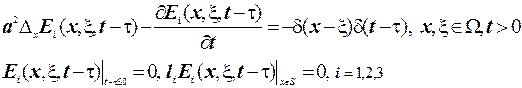(3.20)

Еквівалентне визначення можна надати у вигляді

Означення 4 Функцію 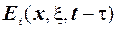будемо називати функцією Гріна першої, другої або третьої граничної задачі рівняння теплопровідності в області 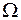с границею 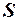і 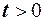, якщо вона може бути представлена у вигляді 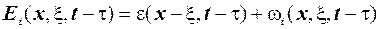, де перший доданок є фундаментальним розв’язком оператора теплопровідності, а другий є розв’язком наступної граничної задачі

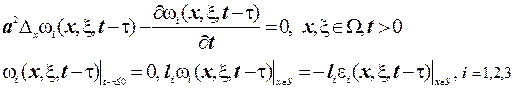(3.20’)

Вивчимо властивості функції Гріна.

Легко бачити, що функція Гріна граничних задач рівняння теплопровідності з аргументами 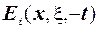задовольняє спряженому диференціальному рівнянню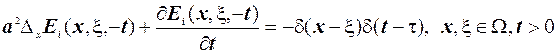

Покажемо, що функція є також симетричною функцією своїх перших двох аргументів. Для цього запишемо співвідношення яким задовольняє функція Гріна:

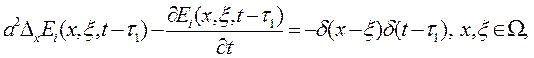
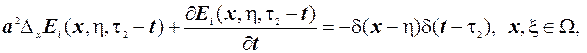
Перше рівняння помножимо на 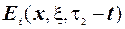, друге рівняння помножимо на 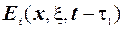, віднімемо від першого друге і проінтегруємо 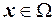по і по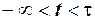

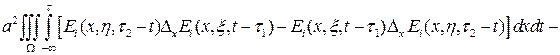
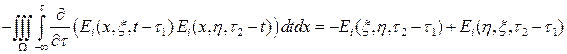
В результаті застосування другої формули Гріна до першого інтегралу в лівій частині рівності і обчислення другого інтегралу лівої частини, отримаємо:

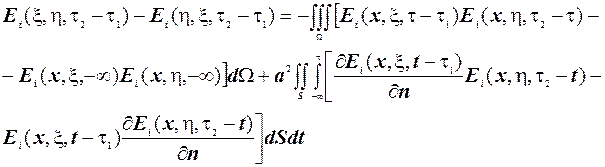
Обираючи 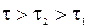, отримаємо з урахування граничних і початкових умов для функції Гріна, що інтеграли в правій частині останньої рівності дорівнює нулю.

Таким чином маємо симетричність функції Гріна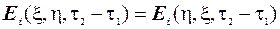

Для отримання формули інтегрального представлення розв’язку граничної задачі, запишемо граничну задачу теплопровідності в змінних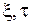

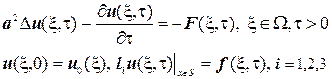(3.19’)

Та рівняння для функції Гріна по змінних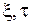

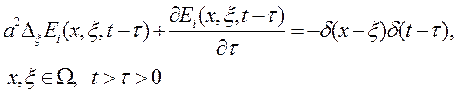(3.21)

Рівняння (3.19’) помножимо на 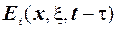, а рівняння (3.21)помножимо на 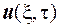, віднімемо від першого рівняння друге і про інтегруємо 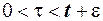по та по .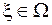

Отримаємо наступне співвідношення:

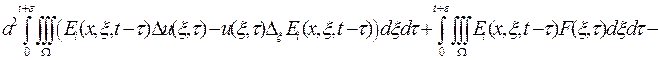
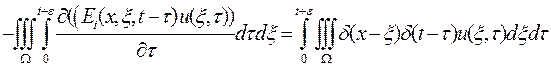
Після застосування другої формули Гріна до першого інтегралу, обчислення третього інтегралу при 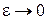отримаємо наступну проміжну формулу:

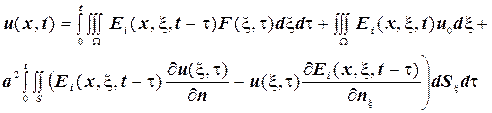
Враховуючи відповідні граничні умови, яким задовольняє розв’язок на границі поверхні 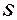отримаємо для першої граничної задачі:

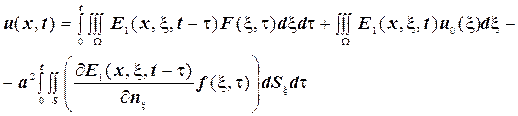(3.22)

Для другої та третьої граничних задач отримаємо

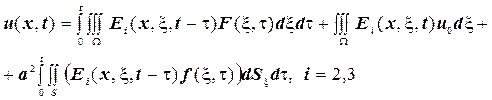(3.23)

Дата добавления: 2014-01-04