Лекція 22 Тема. Основи теорії масового обслуговування

План

Лекція 21 Тема 21. Важливі класи випадкових процесів

1. Поняття про випадковий процес.

2. Класифікація випадкових процесів.

3. Основні характеристики випадкового процесу: математич­не сподівання, дисперсія, кореляційна функція, сумісна кореляційна функція.

4. Випадковий процес, стаціонарний у широкому сенсі. Ана­ліз кореляційної функції. Ергодичність.

5. Поняття марковського випадкового процесу.

6. Рівняння Колмогорова-Чепмена (Феллера).

Процес отримання і використання інформації є процесом нашого пристосування до випадковостей зовнішнього середовища і нашої життєдіяльності в цьому
середо- вищі.

Н. Вінер

При вивченні багатьох явищ стикаються з вивченням випадкових величин, що змінюються з часом. Прикладів таких випадкових величин можна привести чимало: вага людини, кількість часу, який студент витрачає протягом семестру на самостійну роботу, довжина черги в студентському кафе, рейтинг кандидата в президенти країни, кількість відвідувачів офіційного сайта університету тощо.

Випадковими функціями називають випадкові величини, що змінюються у процесі проведення досліду (спостереження або експерименту).

Означення. Теорія випадкових функцій (випадкових процесів) – це розділ вищої математики, що вивчає випадкові явища в динаміці їх розвитку. Ця теорія широко використовується у теорії інформації, автоматичного керування, при аналізі та плануванні фінансового стану підприємства, при обробці та передачі сигналів радіоелектронних пристроїв, у теорії масового обслуговування тощо.

Означення. Кажуть, що на деякій множині 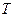дійсних чисел задана випадкова функція (ВФ) 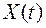, якщо кожному значенню 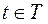, ставиться у відповідність випадкова величина 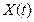. Або по іншому: випадковою функцією 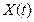називають випадкову функцію від невипадкового аргументу .

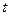Означення. Випадковим процесом називається випадкова функція, якщо аргумент 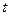визначається як час. Випадковий процес – це сімейство випадкових величин 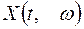, що задані на одному й тому ж просторі елементарних подій 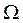, що залежить від параметра 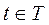. Випадковий процес позначається таким чином: 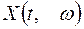, 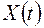або .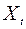

Випадковий процес може бути заданий формулою у випадку, якщо відомий вид випадкової функції і випадкові величини, що задають параметри ВФ, задані аналітично.

Приклад 21.1. Випадкова функція 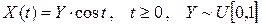- ВФ, що має рівномірний розподіл, є випадковим процесом.

Означення. Зрізом випадкового процесу називають випадкову величину 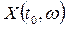, в яку перетворюється випадковий процес 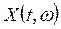при фіксованому значенні параметра .

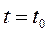Означення. Реалізацією або траєкторією випадкового процесу називають невипадкову функцію від часу 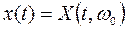при фіксованому 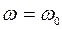, тобто конкретний вигляд, що його приймає випадковий процес у результаті досліду або спостереження. Реалізації ВП позначають через 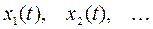, де індекс вказує на номер досліду або спостереження.

На рисунку 21.1 подано три реалізації 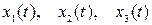випадкового процесу при 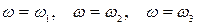. Кожна така траєкторія є звичайною функцією 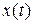. Три відображені на малюнку точки - це значення випадкової величини 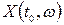в трьох дослідах.

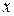
0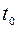

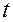
Рис. 21.1

Так, якщо в розглянутому прикладі 21.1 ВВ 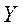в першому досліді прийняла значення 1, в другому – (–1), в третьому – 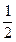, то отримуємо три реалізації випадкового процесу: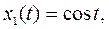 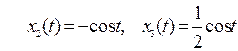– невипадкові функції. Якщо в цьому прикладі зафіксувати момент часу, наприклад 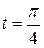, то отримуємо переріз: 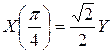– випадкова величина.

Означення. Одновимірним законом розподілу випадкового процесу 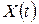називається функція 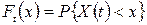. Ця характеристика не є повною (вичерпною) для випадкового процесу. Випадковий процес 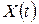являє собою сукупність усіх реалізацій при різних значеннях 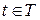, тому для повного описання необхідно розглядати сумісну функцію розподілу реалізацій (перерізів) процесу:

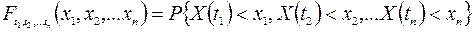
це скінченновимірний закон розподілу випадкового процесу в моменти 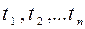, отже розглядаємо багатовимірну випадкову величину .

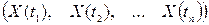Зауваження. Поняття випадкового процесу є узагальненням поняття системи випадкових величин у випадку, коли кількість цих величин нескінченна.

3. Класифікація випадкових процесів.

Випадковий процес, що розглядається в будь-якій фізичній системі, 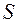являє собою випадкові переходи системи з одного стану в інший. Залежно від множини цих станів 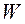, від множини 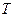значень аргументу 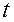всі випадкові процеси розподіляють на класи:

– Дискретний процес (дискретний стан) з дискретним часом.

– Дискретний процес з неперервним часом.

– Неперервний процес (неперервний стан) з дискретним часом.

– Неперервний процес з неперервним часом.

У першому та третьому випадках множина станів 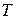є дискретною, тобто аргумент 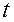приймає лише дискретні значення 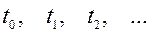(зазвичай, 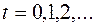); у першому випадку множи­на значень випадкової величини, тобто 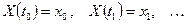– дискретна множина (тобто множина 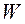є скінченною або зліченною), у третьому випадку множина 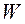є незліченною, тобто переріз випадкового процесу в будь-який момент часу 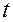являє собою неперервну випадкову величину.

У другому та четвертому випадках множина 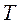неперервна, в другому випадку множина станів 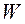є скінченною або зліченною, а в четвертому 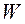незліченна множина.

Наведемо приклади відповідних класів процесів.

1. Тенісист може отримати певну кількість очок під час турніру, матчі відбуваються у певний момент (відповідно до розкладу турніру) часу 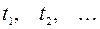Випадковий процес 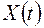— кількість забитих голів до моменту часу .

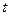2. 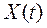— кількість отриманих абонентом телефонних дзвінків протягом дня до моменту .

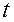3. У певні моменти часу 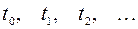фіксується ціна на пальне 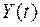. Це випадковий процес неперервного типу з дискретним часом.

4. Серцевий тиск людини .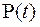

Вивчають випадкові процеси залежно від їх типу різними методами.

3. Основні характеристики випадкових процесів.

Як і у випадку випадкових величин, випадковим процесам ставляться у відповідність певні числові характеристики. Інформації про числові характеристики процесу достатньо для розв’я­зання багатьох практичних задач. Ускладнення, порівняно з випадковими величинами, полягає у тому, що числові характеристики випадкових процесів представляються в загальному випадку не числами, а функціями.

Означення. Математичним сподіванням ВП 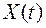називають невипадкову функцію 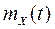, яка в будь-який момент часу 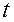дорівнює математичному сподіванню відповідного перерізу випадкового процесу, тобто

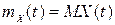(21.1)

Позначають математичне сподівання 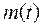або .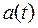

Як і випадку математичного сподівання випадкової величини, функція 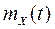характеризує поведінку ВП в середньому. Геометрична інтерпретація математичного сподівання така: це «середня крива», навколо якої розташовані графіки функцій реалізацій випадкового процесу (рис. 21.2).

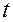
Рис. 21.2

Основні властивості математичного сподівання та невипадкових функцій дають змогу сформулювати основні властивості математичного сподівання випадкових процесів.

1. Математичне сподівання невипадкової функції дорівнює самій невипадковій функції, тобто

.

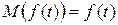2. Невипадковий множник можна винести за знак математичного сподівання випадкового процесу, тобто

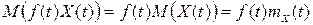
3. Математичне сподівання алгебраїчної суми двох випадкових процесів дорівнює алгебраїчній сумі математичних сподівань доданків, тобто

.

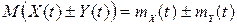Зауваження. Зафіксувавши аргумент 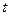при переході від випадкового процесу до випадкової величини (тобто до зрізу випадкового процесу), можна знайти математичне сподівання цього процесу.

Таким чином, якщо ВП 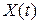при даному 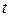є неперервна випадкова величина з щільністю розподілу 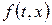, то його математичне сподівання можна знайти за формулою:

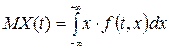. (21.2)

Приклад 1. Знайти математичне сподівання випадкового про­цесу 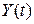, що задається формулою 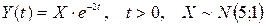, (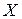– випадкова величина розподілена за нормальним законом з ).

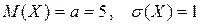Розв’язання. 1 спосіб. Щільність розподілу ВВ Х має вигляд 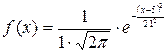, використовуючи формулу (2) обчислюємо: ,

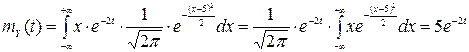так як .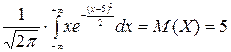

Власне результат можна було б отримати і в інший спосіб, використовуючи властивість 2 математичного сподівання випадкового процесу:

.

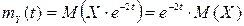Але відповідно до умови задачі 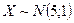, тобто 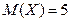і відповідно .

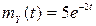Означення. Дисперсією випадкового процесу 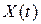називається невипадкова функція 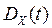, яка при кожному значенні 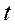дорівнює дисперсії відповідного зрізу

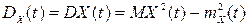(21.3)

Дисперсія 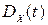випадкового процесу 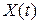характеризує розсіювання можливих значень випадкового процесу навколо його математичного сподівання.

Разом з дисперсією ВП розглядається і така числова характеристика як середнє квадратичне відхилення 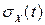, що визначається рівністю

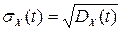. (21.4)

Розмірність функції середнє квадратичне відхилення збігається з розмірністю ВП .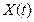

Сформулюємо основні властивості дисперсії випадкового процесу:

1. Дисперсія невипадкової функції дорівнює нулю, тобто

.

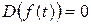2. Дисперсія ВП є невід’ємною функцією:

.

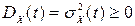3. Дисперсія добутку невипадкової функції на випадкову функцію дорівнює добутку квадрату невипадкової функції на дисперсію випадкової функції, тобто

.

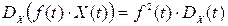4. Дисперсія суми ВП та невипадкової функції дорівнює дис­персії ВП, тобто

.

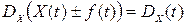Приклад 21.2. Використовуючи умови прикладу 21.1, знайти дисперсію та середнє квадратичне відхилення.

Розв’язання. Знайдемо дисперсію, використовуючи властивість 3: 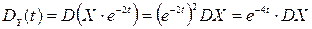, за умови 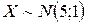, тобто 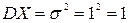. Тому 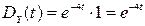, відповідно .

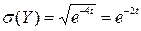Математичне сподівання та дисперсія не є вичерпуючими характеристиками випадкового процесу, знаючи лише ці дві характеристики, наприклад, не можна зробити висновок про залежність двох або більше перерізів ВП. Саме для характеризації зв’язку між різними перерізами ВП використовують кореляційну функцію. Аналогом даної числової характеристики у випадкових величинах є коваріація, або кореляційний момент:

,

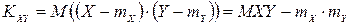що характеризує ступінь зв’язку між двома випадковими величинами 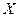та .

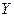Означення. Кореляційною (коваріаційною, автоковаріаційною, авто- кореляційною) функцією ВП 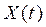називають невипадкову функцію двох аргументів 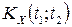, яка при кожній парі значень 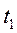та 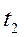дорівнює кореляційному моменту (коваріації) відповідних перерізів 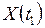та :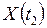

,

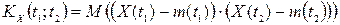або

,

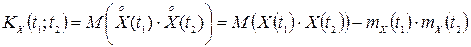де 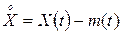– центрована випадкова функція.

Сформулюємо основні властивості кореляційної функції 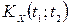випадкового процесу .

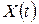1. Кореляційна функція при однакових значеннях аргументів дорівнює дисперсії випадкового процесу, тобто

.

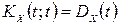Доведення. Дійсно,

.

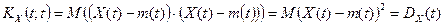Зауваження. Дана властивість дозволяє вважати математичне сподівання та кореляційну функцію головними числовими характеристиками випадкового процесу.

2. Кореляційна функція не змінюється при перестановці аргументів місцями, тобто .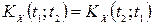

3. Якщо до випадкового процесу додати випадкову функцію, то кореляційна функція не зміниться, тобто, якщ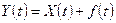о , то

.

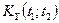
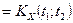Доведення. Відповідно до властивості математичного сподівання 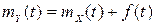, то 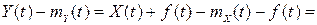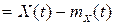, звідси безпосередньо випливає, що = .

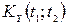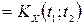4. Модуль кореляційної функції не перевищує добуток середніх квадратичних відхилень, тобто

.

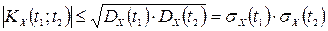Ця властивість випливає з відповідної властивості кореляційного моменту двох ВВ та з урахуванням першої властивості кореляційної функції ВП.

5. При множенні ВП 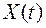на невипадковий множник 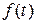її кореляційна функція помножиться на добуток 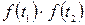, тобто, якщ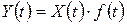о , то

.

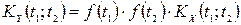Поряд з кореляційною функцією ВП розглядається також нормована кореляційна функція (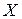або нормована автоковаріаційна функція) .

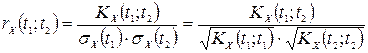За своїм імовірністним змістом 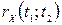є певним аналогом коефіцієнту кореляції для двох ВВ, але не є сталою величиною, а залежить від аргументів 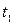та .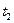

Безпосереднім наслідком означення нормованої автокореляційної функції та основних властивостей кореляційної функції ВП є такі властивості :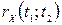

1. .

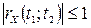2. .

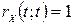3. .

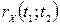
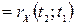Приклад 21.3. Використовуючи умови прикладу 21.1, знайти кореляційну та нормовану кореляційну функцію випадкового процесу .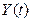

Розв’язання. Використовуючи означення кореляційної функції випадкових процесів, отримуємо:

= .

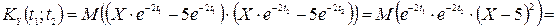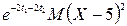
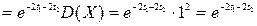Тобто 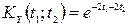. Відповідно .

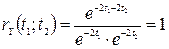Для визначення ступені взаємозв’язку зрізів двох випадкових процесів використовують кореляційну функцію зв’язку або взаємну кореляційну функцію.

Означення. Взаємною кореляційною функцією двох випадкових процесів 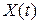та 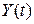називається невипадкова функція 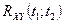двох незалежних аргументів 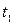та 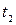, яка для кожної пари значень 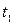та 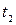дорівнює кореляційному моменту двох перерізів 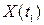та :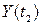

.

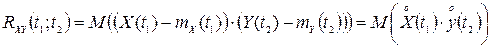Означення. Два випадкових процеси 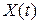та 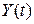називаються некорельованими, якщо їх взаємна кореляційна функція тотожньо дорівнює нулю, тобто, якщо 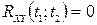для будь-яких 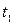та 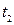. У випадку, коли 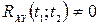випадкові процеси 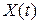та 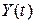називаються корельованими (пов’язаними).

Сформульовані вище властивості кореляційного моменту дають можливість сформулювати ряд властивостей взаємної кореляційної функції.

1. При одночасній перестановці індексів та аргументів взаємна кореляційна функція не змінюється, тобто

.

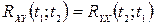2. Модуль взаємної кореляційної функції двох випадкових процесів не перевищує добутку їх середніх квадратичних відхилень, тобто

.

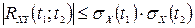3. Кореляційна функція не зміниться, якщо до випадкових процесів 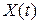та 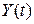додати невипадкові функції 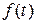та 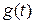відповідно, тобто 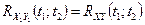, тут .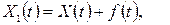

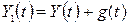4. Невипадкові множники можуть бути винесені за знак кореляційної функції, тобто, якщ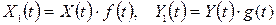о , то

.

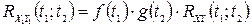5. Якщ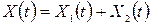о , то

.

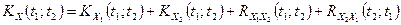6. Якщо випадкові процеси 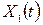та 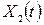некорельовані, то ко­реляційна функція їх суми дорівнює сумі їх кореляційних функцій:

.

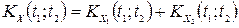Оцінюють ступінь залежності перерізів двох випадкових процесів за допомогою нормованої взаємної кореляційної функції 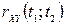, що визначається рівністю:

.

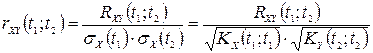Функція 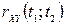має такі самі властивості, як і функція 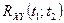за виключенням другої властивості, яка заміняється на наступну: .

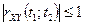Приклад 21.4. Знайти взаємну кореляційну функцію двох випадкових процесів 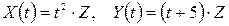, де 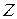– випадкова величина, для якої .

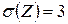Розв’язання. Обчислимо 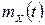та :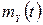

.

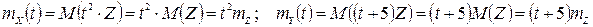Використовуючи означення взаємної кореляційної функції випадкових процесів, маємо:

.

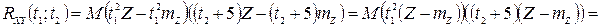
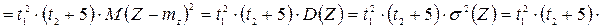
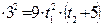Остаточно .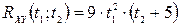

4. Випадковий процес, стаціонарний у широкому сенсі.

Важливим класом випадкових процесів є стаціонарні ВП, тобто такі, що не змінюють свої характеристики з часом. Ці процеси мають вигляд неперервних випадкових коливань навколо деякого середнього значення. Такими процесами є тиск людини, коливання напруги в електричній мережі тощо.

Означення. Випадковий процес 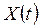називається стаціонарним у широкому сенсі, якщо його математичне сподівання 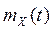є сталою, а кореляційна функція 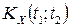залежить лише від різниці аргументів, тобто

.

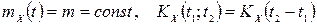З означення стаціонарного в широкому сенсі випадкового процесу випливає, що його кореляційна функція є функцією одного аргументу, тобто

.

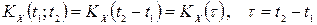Нижче сформульовані основні властивості кореляційної функції стаціонарного випадкового процесу СВП.

1. Дисперсія СВП є величиною сталою і дорівнює значенню кореляційної функції в нулі, тобто

.

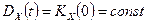2. Кореляційна функція СВП є функцією парною, тобто

.

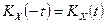3. Модуль кореляційної функції СВП не перевищує її значення при 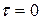, тобто

.

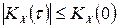4. Нормована кореляційна функція СВП є невипадковою функцією аргументу :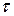

.

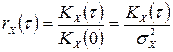Має місце нерівність .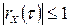

Більшість СВП мають важливу для практики властивість ергодичності. Суть цієї властивості полягає в тому, що по одній, достатньо тривалій реалізації, можна зробити висновок про всі властивості процесу, так само як по будь-якій кількості реалізацій. Тобто окремі характеристики СВП, а саме 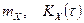можуть бути визначені як відповідно середнє по часу для однієї реалізації але досить тривалої.

Зауваження. Ергодичні ВП є стаціонарними у вузькому сенсі, зворотне твердження взагалі неправильне.

Достатньою умовою ергодичності ВП 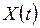щодо математичного сподівання та кореляційної функції є прямування до нуля його кореляційної функції при 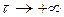, тобто .

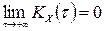Як оцінки характеристик ергодичних СВП приймають усереднене за часом значення

.

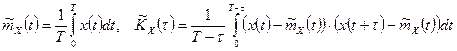Інтеграли в правих частинах рівностей на практиці розраховують наближено.

Випадкові процеси 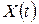та 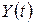називають стаціонарно пов’язаними, якщо їх взаємна кореляційна функція 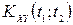залежить лише від .

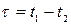Як приклад стаціонарного процесу розглянемо випадковий процес 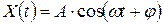- гармонійне коливання. Розрахунки дають ,

.

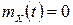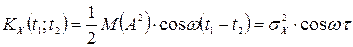5. Поняття марковського випадкового процесу.

Серед випадкових процесів особливе місце займають Мар­ковські випадкові процеси (МВП).

Розглянемо деяку фізичну систему 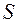, в якій відбувається випадковий процес. З плином часу вона може під впливом випадкових факторів переходити з одного стану в інший.

Означення. Випадковий процес називається процесом з дискретними станами, якщо множина всіх його можливих станів 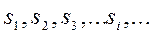є зліченною або скінченною, а перехід з одного стану в інший відбувається стрибково, переходи можливі лише в певні моменти часу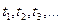

Якщо переходи можливі в будь-який момент часу, тобто моменти переходу з одного стану в інший випадкові, то процес називається процесом з неперервним часом.

Означення. Випадковий процес з дискретними станами називається Марковським (МП),якщо для будь-якого моменту часу 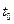умовна ймовірність кожного з станів системи 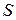в майбутньому (тобто при 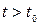) залежить лише від її стану в теперішній час (тобто при 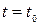) і не залежить від того, коли і як система прийшла в цей стан (тобто від того, які були стани системи 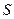в минулому ).

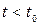Коротко: майбутнє МП залежить лише від теперішнього стану, і не залежить від минулих станів системи.

Марковський процес називають також процесом без післядії: майбутнє в ньому залежить від минулого лише через теперіш­нє, тобто ймовірність системи 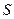потрапити в стан 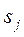в момент часу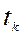 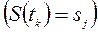залежить лише від стану 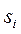, в якому система знаходиться в момент часу :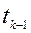

,

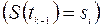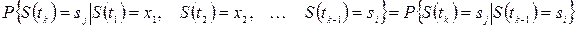де 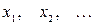- це можливі стани системи .

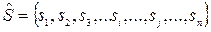Марковський процес є стохастичною математичною моделлю багатьох процесів у біології (розподіл епідемій, ріст популяцій), у фізиці (радіоактивний розпад), у теорії масового обслуговування. У теорії систем масового обслуговування множина станів системи визначається кількістю каналів (вузлів обслуговування). Це можуть бути вузли обслуговування, кабінети лікарів, кількість кас в супермаркеті тощо. Переходи між станами системи 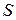відбуваються під впливом вхідного потоку подій (тобто кількості заявок, пацієнтів, покупців тощо), які є найпростішими, тобто пуасонівськими. Детальніше про це у наступній лекції.

Випадкові процеси з дискретними станами зручно відображати в формі так званого графа станів. У ньому стани системи 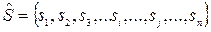зображаються в формі вершин графа, а можливі безпосередні переходи з стану в стан – орієнтованими дугами графа, що з’єднують відповідні вершини – стани.

Приклад 21.5. Побудувати граф станів випадкового процесу: локальна мережа у випадковий момент часу може вийти з ладу, вона перевіряється в певні моменти часу, наприклад, кожних десять хвилин. У разі необхідності відбувається налагодження мережі. Є два типи неполадок – незначні та суттєві (такі, що вимагають довгострокового технічного обслуговування).

Розв’язання. Дана система 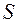може перебувати в одному з трьох станів 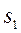– локальна мережа працює; 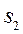– у мережі відбувся несуттєвий збій, їй необхідне налагодження; 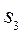– відбувся нас­тільки суттєвий збій, що мережа знаходиться у процесі тривалого налагодження.

Граф має вигляд, зображений на рис. 21.3. Процес являє собою випадкове блукання системи 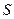за станами, час 10 хвилин – це крок процесу.

Реалізації ВП блукання системи може мати зокрема такий вигляд:

.

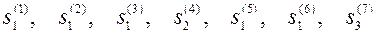Цей перелік станів визначає наступне: при 1-му, 2-му, 3-му огляді система була справна; при 4-му несправна і знаходиться в процесі налагодження; при 5-му, 6-му – справна; при 7-му – вимагає суттєвого ремонту.

Рис 21.3

Для описання ВП з дискретними станами використовують ймовірності станів системи 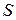, тобто значення 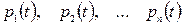, де 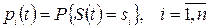- ймовірність того, що в момент часу 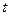система знаходиться в стані 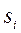, 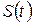– випадковий стан системи 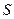в момент часу .

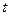Очевидним є той факт, що для будь-якого моменту 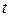сума ймовірностей всіх станів дорівнює 1 (як сума ймовірностей повної групи подій):

.

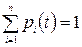6. Рівняння Колмогорова-Чепмена.

Нехай в деякій системі 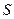відбувається СВП з дискретними станами 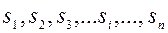та дискретним часом, тобто перехід системи з одного стану в інший відбувається тільки в певні моменти часу 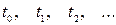Ці моменти називають кроками процесу (зазвичай, різниці сусідніх моментів спостережень 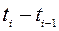дорівнюють сталому числу – ширині кроку, що приймається за одиницю часу); початок процесу визначається моментом часу .

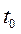Цей випадковий процес можна розглядати як послідовність (ланцюг) подій 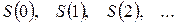(де 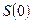– початковий стан системи, тобто перед першим кроком; 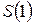– стан системи після 1-го кроку; 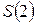– після 2-го кроку і т.д.). Тобто це послідовність подій виду .

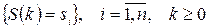Означення. Марковський випадковий процес з дискретними станами та дискретним часом називають ланцюгом Маркова.

Ланцюг, в якому умовні ймовірності станів в майбутньому залежать лише від стану на даному, останньому кроці (і не залежать від попередніх), називають простим ланцюгом Маркова.

У даному курсі розглядають лише прості ланцюги Маркова. Основним завданням при дослідженні простих ланцюгів Маркова є обчислення ймовірностей станів системи:

,

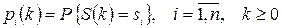де 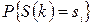– безумовна ймовірність того, що на 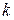-му кроці система буде знаходиться у стані .

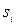Для обчислення безумовної ймовірності необхідно знати початковий розподіл ймовірностей 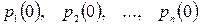, тобто ймовірності станів 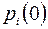в момент початку процесу 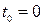та перехідні ймовірності 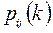– марківського ланцюга на 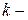му кроці.

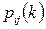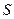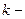Означення. Перехідною ймовірністю називають умовну ймовірність переходу системи на му кроці в стан 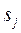, якщо відомо, що на попередньому 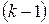кроці вона була в стані 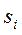, тобто

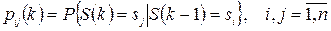
тут перший індекс визначає номер попереднього, а другий – номер наступного стану.

Означення. Ланцюг Маркова називається однорідним, якщо 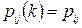, тобто умовні ймовірності 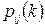не залежать від номера спостереження.

Далі розглядатимемо лише однорідні ланцюги, що можуть бути задані за допомогою вектора 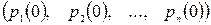– ймовірностей станів у початковий момент часу 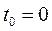та матриці

,

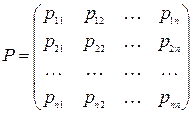що називаються матрицею перехідних ймовірностей.

Елементи матриці 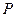мають такі властивості:

1. Усі її елементи невід’ємні .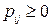

2. Сума ймовірностей кожного рядку перехідної матриці дорівнює одиниці (як ймовірності переходу з одного стану 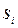в будь-який можливий стан 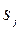– утворюють повну групу подій): .

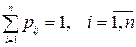Твердження. Матриця переходу ланцюга Маркова за 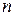кроків: 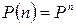.Має місце формула Колмогорова-Чепмена.

Приклад 21.7. Задано матрицю перехідних ймовірностей 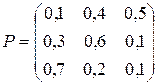. Знайти матриці перехідних ймовірностей за два кроки, за чотири кроки.

Розв’язання. За формулою 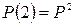маємо:

.

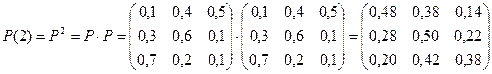Відповідно для переходу за 4 кроки маємо:

.

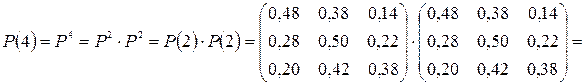
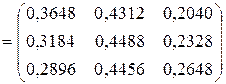Зауважимо, що ланцюг Маркова є узагальненням схеми Бер­нуллі у випадку залежних випробувань; незалежні випробування є частинним випадком ланцюга Маркова. Під «подією» розуміють стан системи, а під «випробуванням» – зміну її стану.

Якщо «випробування» незалежні, то поява певної події в будь-якому досліді не залежить від результатів раніше проведених випробувань.

Словник-мінімум до лекції 21

Random (stochastic) process	Випадковий процес
Random process with stationary increments	Випадковий процес зі стаціонарними приростами
Correlation function	Коряляційна функція
Autocovariance assembly language	Автоковаріація
Markovian process	Марковський процес
Markov chain (Markovian chain)	Ланцюг Маркова
Transition probability	Ймовірність переходу
Transition probability matrix	Матриця перехідних ймовірностей
Correlated processes	Корельовані процеси
Stationary to wide extent process	Процес стаціонарний у широкому сенсі
Stationary in a restricted sense process	Стаціонарний у вузькому сенсі процес
Ergodic property	Ергодична властивість
Discrete state	Дискретний стан
Сonvergence	Збіжність
Linear transformation	Лінійне перетворення
Wiener random process	Вінеровський випадковий процес
Spectral factorization	Спектральний розклад

Дата добавления: 2014-01-04