Граничні характеристики ефективності функціонування одноканальної СМО з очікуванням

	Гранична характеристика	Позначення (формула)
1.	Середній час обслуговування однієї вимоги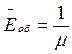
2.	Навантаженість (графік) системи
3.	Ймовірності станів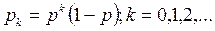
4.	Ймовірність відмови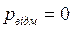
5.	Ймовірність того, що замовлення буде прийнято в систему
6.	Відносна пропускна здатність СМО
7.	Абсолютна пропускна здатність СМО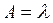
8.	Інтенсивність вихідного потоку Пвих задоволених вимог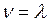
9.	Середня кількість вимог у черзі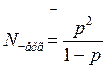
10.	Середня кількість замовлень в обслуговуванні
11.	Середнє число замовлень в системі
12.	Середній час очікування замовлення в черзі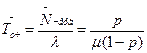
13.	Середній час перебування вимоги в системі (як в черзі, так і під обслуговуванням)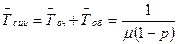

Числові характеристики багатоканальної СМО з очікуванням вираховуються за значно складнішими формулами (список рекомендованої літератури 10, 35).

Системи масового обслуговування з чергою та обмеженням на її довжину відрізняються від попередньої тим, що ця система може знаходитись в одному з n+m+ 1 станів. У станах: s_k (k= 0,1,… n) – k каналів зайняті та черги в системі немає; в станах s_k+i (i= 1,… m) – i замовлень стоять у черзі. Довжина черги не може перевищувати числа m (m ≥1). Замовлення, що надійшло в СМО в момент часу, коли в черзі вже є m замовлень,отримує відмову і не буде задоволене. Показники ефективності таких одноканальних та багатоканальних СМО ви можете знайти в літературі (список рекомендованої літератури 10, 35).

5. Поняття про статистичне моделювання (Метод Монте-Карло).

Універсальний метод статистичного моделювання – метод Монте-Карло, дозволяє проаналізувати роботу систем масового обслуговування у випадку, коли аналітичні методи не можуть бути використані. Суть даного методу полягає в тому, що замість аналітичного опису СМО використовують так зване «розігрування» випадкового процесу, що відбувається в СМО за допомогою спеціальної процедури. В результаті кожного разу випадковий процес з кожним розіграшем приймає іншу реалізацію і, по суті, отримується новий статистичний матеріал.

Наведемо приклад. Підприємець має бажання проаналізувати черги, що виникають на автомийці, для прийняття рішення про необхідність збільшення кількості боксів для миття авто. Час під’їзду авто та час їх обслуговування мають випадковий характер та їх розподіли можуть бути відтворені на основі вже існуючої інформації. Як результат взаємодії цих випадкових процесів виникає черга. Відповідно до методу Монте-Карло влаштовують (раціональніше з використанням вбудованої в сучасні пакети прог­рам функції) випадковий перебір усіх можливих станів систем із різним числом клієнтів у день, часом їх обслуговування тощо, зберігаючі ті самі характеристики обслуговування, якби вони відбувалися реально.

Зауважимо, що у разі моделювання випадкових явищ за методом Монте-Карло випадковість використовується як апарат дослідження.

Словник-мінімум до лекції 22

Іntensity	Інтенсивність
Queueing theory, theory of waiting lines (systems)	Теорія масового обслуговування
Flow of events	Потік подій
Exponential arrivals	Пуасонівський вхідний потік
Waiting system	Система з очікуванням
Call-queueing system	Система з накопиченням
Single-channel queuing	Одноканальна система обслуговування
Multichannel system	Багатоканальна система
Statistical modeling	Статистичне моделювання
Output stream	Вихідний потік
Off-hook channel	Зайнятий канал
Unoccupied channel	Вільний канал
Load-carrying system	Навантажена система
Service time	Час обслуговування
Sojourn time	Час перебування
State probability	Ймовірність стану
Carrying capacity, network capacity	Пропускна здатність

Дата добавления: 2014-01-04