Зв'язок між потенціалом і вектором напруженості

У декартовій системі координат вектор напруженості можна представити наступним чином: 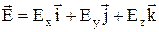. Але , , . Після підстановки одержуємо: . Величина, що стоїть у дужках, являє собою градієнт потенціалу або . У підсумку одержуємо формулу, що зв'язує напруженість і потенціал:

.

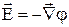Напруженість електростатичного поля дорівнює градієнту потенціалу, узятого зі знаком «мінус». Якщо поле однорідне і переміщення відбувається уздовж лінії напруженості, то остання формула здобуває вигляд:

або .

Еквіпотенціальними поверхнями називаються поверхні рівного потенціалу. Оскільки 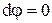, то А_ел=0 і вектор переміщення заряду уздовж еквіпотенціальних поверхонь перпендикулярний вектору напруженості в будь-якій точці.

Висновок: Еквіпотенціальні поверхні в будь–якій точці перпендикулярні вектору напруженості в даній точці.

Потенціальна енергія взаємодії двох точкових зарядів. Нехай заряд q₂ знаходиться у полі заряду q₁ на відстані r від нього. Тоді можна записати:

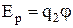, но .

Після підстановки одержуємо: .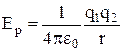

Електричний диполь.

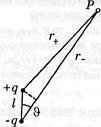Електричний диполь – це система з двох однакових за модулем і різнойменних точкових зарядів +q і –q, що знаходяться на деякій відстані l один від одного, причому ця відстань у багато разів менше відстані, на якому оцінюється дія диполя.

Визначимо потенціал і напруженість поля диполя у точці Р. Відповідно до принципу суперпозиції:

.

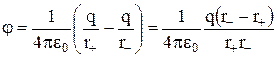Оскільки r << l, то 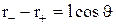, а 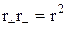, де r – відстань від точки Р до диполя. У підсумку одержуємо:

,

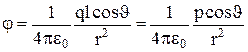де – електричний момент диполя. Цій величині зіставляють вектор, спрямований по осі диполя від негативного заряду до позитивного:

,

де q > 0 і 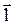- вектор, спрямований у ту ж сторону, що і .

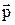Визначимо напруженість поля диполя. Для цього обчислимо проекції вектора напруженості на два взаємно перпендикулярних напрямки – уздовж ортів і :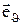

, .

Модуль вектора напруженості знайдемо за теоремою Піфагора:

.

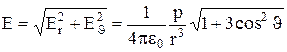Напрямок вектора напруженості стосовно напрямку 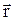визначається як: .

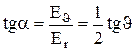Сила, що діє на диполь. Помістимо диполь у зовнішнє неоднорідне електричне поле. Неха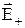й и 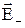– напруженості зовнішнього поля в точках, де розташовані позитивний і негативний заряди диполя. Тоді результуюча сила, що діє на диполь, дорівнює:

,

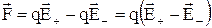де 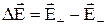– збільшення вектора напруженості на відрізку, довжина якого дорівнює довжині диполя. Внаслідок малості цього відрізку можна записати:

.

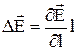Після підстановки у формулу сили одержуємо:

.

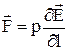Момент сил, що діють на диполь. Нехай диполь знаходиться в зовнішньому електрополі, напруженість якого 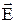. Сили, що діють на позитивний і негативний заряди диполя, утворюють пари: и 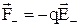, плече якої дорівнює , тобто залежить від орієнтації диполя відносно поля 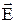. Модуль кожної з цих сил дорівнює , і на диполь буде діяти механічний момент М, обумовлений добутком на плече пари, тобто:

.

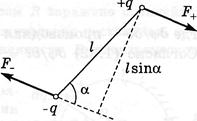
Отриману формулу можна представити у векторному вигляді як

.

Цей момент сил намагається повернути диполь так, щоб його електричний момент 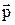встановився за напрямком зовнішнього поля 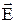. Таке положення диполя є стійким. У неоднорідному електричному полі диполь буде поводитися таким чином: під дією моменту сил диполь буде намагатися встановитися по полю, а під дією результуючої сили – переміститися в напрямку, де Е за модулем більше. Обидві рухи будуть відбуватися одночасно.

Енергія диполя в полі. Енергія точкового заряду q у зовнішнім полі дорівнює: , де j – потенціал поля в точці знаходження заряду q. Диполь – це система з двох зарядів, тому його енергія в зовнішнім полі визначається як:

.

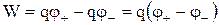Збільшення потенціалу на довжині диполя дорівнює: , де 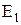– проекція вектора напруженості на напрямок l. У загальному вигляді можна записати: . В остаточному підсумку одержуємо:

.

З цієї формули випливає, що мінімальну енергію диполь має в положенні стійкої рівноваги, коли a = 0. При відхиленні від цього положення виникає момент зовнішніх сил, який повертає диполь до положення рівноваги.

Дата добавления: 2014-01-04