Энергия колебательных уровней определяется выражением

Е_кол = , (2.23)

где V = 0,1,2, и т.д. - колебательное квантовое число, 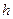- постоянная Планка.

При V = 0 формула дает энергию нулевых колебаний равную 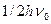. Значение 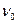совпадает с классической частотой малых упругих колебаний

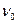
, (2.24)

где 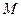- приведенная масса молекул, 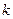- коэффициент упругой связи.

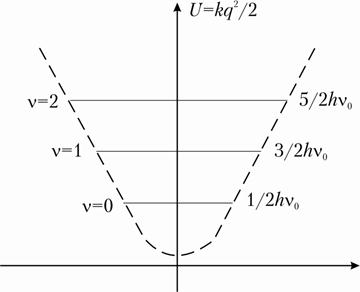
Графически колебательная энергия имеет вид параболы с равноотстоящими уровнями энергии

r

Рис. 2.4. Потенциальная энергия гармонических колебаний , где 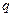- отклонение от положения равновесия, 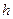- постоянная Планка.

В гармоническом приближении переходы возможны между уровнями энергии, для которых справедливо соотношение

∆V=V '-V= ± 1 (2.25)

где V-колебательные квантовые числа: 0,1,2,3, и т. д.

Реальные потенциальные кривые отличаются от гармони-ческих колебательных и имеют вид, изображенный на рисунке 2.5

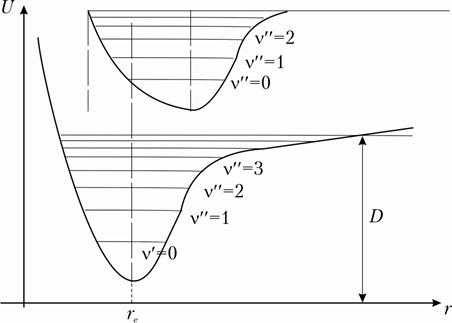
Рис. 2.5 Потенциальная энергия ангармонического осциллятора.

Энергия ангармонического осциллятора определяется выражением

Е_КОЛ=hν₀(V+½) –χ hν₀ (V+½). (2.26)

где χ=4ν/4D << 1 – константа ангармонизма; D – энергия диссоциации.

Из рис.2.5, видно, что при переходе к энергии диссоциации колебательные уровни сгущаются и энергия кванта стремится к нулю. Частоты переходов между уровнями энергии перестают быть равными и переходы становятся возможными в состояния с , т.е., в так называемые, обертоны.

Вращательные уровни энергии. Находятся квантованием энергии вращения. Выражение для вращательной энергии (Е_ВР)

Е_ВР=ВJ(J+1), (2.27)

где J = 0, 1, 2.. вращательное квантовое число; В= ħ²/2I = ħ²/2Mρ² -вращательная постоянная, (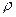- расстояние между ядрами) – момент инерции.

Правила отбора для вращательных переходов определяются соотношением

∆J=J'-J»=0, ±1,…. (2.28)

что дает, так называемые, P-, Q-, R-ветви для ∆J=-1, ∆J=0 и ∆J=1, соответственно.

Для линейных молекул существует дополнительный запрет на переходы с ∆J=0 и Q-ветвь в спектрах отсутствует.

В гармоническом приближении частоты переходов в P- и R- ветвях определяются выражениями:

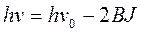для Р-ветви; (2.29)

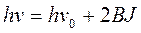для R-ветви.

Обычно с ростом колебательного квантового числа 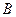уменьшается. Особенно это проявляется в Q-ветви

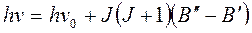, (2.30)

где малая разность 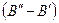для квантовых чисел V приводит к тому, что Q-ветвь гораздо уже, чем P-, R-ветви.

Величина 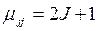характеризует кратность вырождения вращательного уровня. Ее учитывают при определении равновесной концентрации населенностей вращательных уровней.

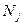= (2.31)

Конкуренция предэкспоненциального числа в выражении 2.31 с экспонециальным приводит к немонотонному характеру заполнения энергетических состояний с различными при заданной температуре.

Дифференцирование выражения (2.31) дает:

.

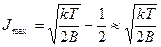Схематическое изображение переходов в 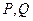и 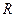-ветвях колебательно-вращательной системы и форма колебательных 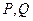и 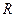-полос показаны на рис. 5.6 и 5.7

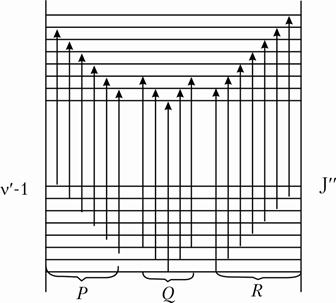
Рис.2.6. Схематическое изображение переходов в P-, Q-, R-ветвях колебательной вращательной системы.

Рис.2.7. Схема P-, Q-, R-переходов колебательной полосы ν '→ ν '-1.

По причине того, что время вращательной релаксации не пре-вышает времени между газокинетическими столкновениями, насыщенность колебательных уровней энергии в системе вращательных подуровней быстро приходит в равновесное состояние.

Дата добавления: 2014-01-04