Лекція 1. Основні поняття про випадкові процеси та їх класифікація

1. Математичне моделювання економічних процесів та його особливості.

2. Значення випадковості та невизначеності в економічних процесах.

3. Класифікація економічно–математичних моделей.

4. Випадкові процеси та їх класифікація.

1. Модель – матеріально або абстрактно представлений об’єкт дослідження, що являє собою такий образ оригіналу, вивчення якого дає можливість отримати певну інформацію про об’єкт–оригінал.

Процес моделювання містить три складові:

– суб’єкт(дослідник);

– об’єкт дослідження;

– модель–образ досліджуваного об’єкта оригінала.

У випадку, коли модель представлена у вигляді системи математичних виразів, говорять про математичне моделювання. Математичне моделювання можливе, коли між елементами об’єкту і елементами моделі можна встановити гомоморфізм.

Інколи виділяють такі етапи розвитку економіко–математичного моделювання:

– математична школа в політекономії(О.Курно; Г.Госсен; Л.Вальрас; Ф.Єджворт; В.Парето; Є.Є.Слуцький; Л.В.Канторович; В.С.Немчинов);

– статичний напрямок (Гарвардська школа – початок ХХ ст.);

– економетрія (П.Чомпа; Р.Фріш).

Математичне модель включає такі елементи:

– характеристики об’єкта, які потрібно визначити (ендогенні змінні):

;

– характеристика зовнішніх щодо об’єкту умов у вигляді змінних (екзогенні змінні):

;

– сукупність внутрішніх параметрів об’єкта–оригіналу (екзогенні змінні):

;

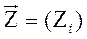Модель представляється у вигляді:

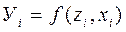(1.1)

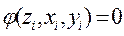або (1.2)

2. Економіка має справу з складними системами, які мають виражені емерджентні властивості. Тому вивчати економічні системи шляхом розчленування їх на елементи неможливо. Велика роль суб’єктивних факторів. Виникають труднощі при зборі економічної інформації, яка повинна бути достатньо повною, достовірною, однорідною, проте, наприклад, забезпечити її хоча б однорідність дуже проблематично(в економіці кожний елемент, наприклад, підприємство має свої особливості).

Внаслідок впливу великої кількості факторів виявити у чистому вигляді економічні залежності в кожному конкретному випадку важко.

Невизначеність економічних процесів зумовлена як великою кількістю зовнішніх факторів, так і обмеженість можливостей щодо їх врахування. З появою комп’ютерної техніки з’явилася можливість врахування значно більшої кількості факторів, на багато збільшилася швидкість обробки економічної інформації. Проте стохастичність – основна особливість економічних процесів.

3. Класифікувати економіко – математичні моделі можна:

– за застосуванням: дискриптивні (описові) та нормативні (управління та регулювання);

– за призначенням: теоретико–аналітичні та прикладні;

– за фактором часу: статичні та динамічні; неперервні та дискретні;

– за математичними залежностями: лінійні та нелінійні;

– за співвідношенням екзогенних та ендогенних змінних: відкриті та закриті.

Найсуттєвішим є поділ на детерміновані та імовірнісні (стохастичні) моделі.

Імовірнісні моделі містять елементи невизначеність та випадковості і базуються на математичних теорії імовірності та теорії випадкових процесів.

4. Випадковий процес – зміна в часі будь–якої економічної системи, зумовлена впливом неконтрольованих випадкових факторів.

Аналітично випадковий або стохастичний процес визначається скінченою дійсною функцією 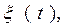,значення якої при різних 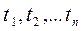набуває випадкову послідовність .

Значення випадкової функції ….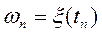називають станами стохастичної системи, а множина – простором станів.

Природа та функція розподілу визначають тип і класи випадкових процесів:

– випадковий процес загального типу: 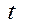та набувають неперервних значень;

– дискретний випадковий процес: 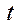неперервно; – дискретно;

– випадкова послідовність загального типу: 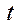– дискретно; – неперервно;

– дискретні випадкові послідовності: 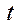та дискретні.

Дата добавления: 2014-01-04