КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Нечітка логіка. Ефективним засобом формалізації і представлення нечітких понять, категорій і знань, у тому числі лінгвістичних висловів є теорія нечіткої множини і заснована
|
|
|
|
Ефективним засобом формалізації і представлення нечітких понять, категорій і знань, у тому числі лінгвістичних висловів є теорія нечіткої множини і заснована на ній нечітка логіка. Отримані в результаті інтерпретації цих описів в термінах нечітких множин логіко-лінгвістичні або нечіткі моделі є конструктивною основою для розробки методів і алгоритмів моделювання процесів в складних системах в умовах невизначеної і неповної інформації. Перевагою нечіткої логіки є можливість використання експертних знань про вирішувані проблеми або структуру об'єкта у вигляді лінгвістичних висловлювань, які представляються нечіткою базою правил: „якщо <входи>, тоді <вихід>".
На жаль, подібні висловлення не можуть бути адекватно формалізовані звичайними математичними методами.
Спроба розвитку формального апарата для залучення часткової належності в теорію множин була почата в середині 60-х років Заде. Він увів поняття нечіткої множини як збірки елементів, які можуть належати цій множині зі ступенем від 0 до 1. Причому 0 позначає абсолютну неналежність, а 1 - абсолютну належність множині). Це було зроблено шляхом застосування поняття функції належності, яке ставить у відповідність кожному елементу універсальної множини число з інтервалу [0,1], що позначає ступінь належності. Поняття функції належності є узагальненням поняття характеристичної функції чіткої множини, що оперує значеннями [0,1]. Тому основні властивості й операції над нечіткими множинами, уведені Заде і його численними послідовниками, є узагальненнями відповідних властивостей й операцій класичної теорії множин.
З метою формалізації нечітких понять і відносин природної мови скористаємося визначенням нечіткої множини.
Визначення 1. Нечітка множина визначається математично як сукупність впорядкованих пар:
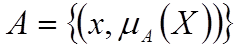
де елементи x є X, а Х - універсальна множина нечіткої множини А, що являє собою всю предметну область визначення відповідних функцій належності 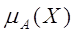 . При цьому функція належності відображає елементи множини Х на множину чисел в інтервалі [0,1 ], тобто
. При цьому функція належності відображає елементи множини Х на множину чисел в інтервалі [0,1 ], тобто 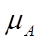 : Х -> [0,1] - представляє собою деяку суб'єктивну міру належності елемента x
: Х -> [0,1] - представляє собою деяку суб'єктивну міру належності елемента x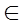 X до нечіткої множини А. Якщо універсальна множина Х охоплює кінцеве число елементів
X до нечіткої множини А. Якщо універсальна множина Х охоплює кінцеве число елементів 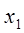 ,
, 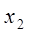 ....
.... 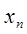 , то нечітку множину А можна представити символічно у вигляді об'єднання:
, то нечітку множину А можна представити символічно у вигляді об'єднання:
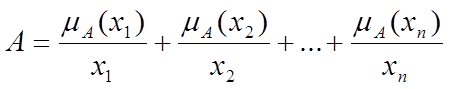
причому, у виразі знак "+" не є операцією складання, а інтерпретується як сума множини елементів (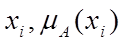 ), які інакше означають присвоєння певним елементом
), які інакше означають присвоєння певним елементом 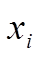 ступеню належності
ступеню належності 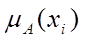 .
.
Поняття функції належності є основним формалізмом теорії нечітких множин, за допомогою якого експертні знання ("Якщо - Тоді") перетворюються на строгі математичні моделі.
Функції належності характеризують суб'єктивну міру упевненості експерта в тому, що деяка величина належить певному нечіткому поняттю - терму, яким характеризується та або інша вхідна (вихідна) змінна. При цьому можна виділити три випадки:
• 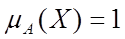 , що означає повну належність елемента x до нечіткої множин А, тобто x
, що означає повну належність елемента x до нечіткої множин А, тобто x 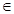 A;
A;
• 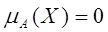 означає відсутність якої-небудь належності х нечіткій множині А;
означає відсутність якої-небудь належності х нечіткій множині А;
• 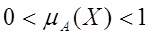 означає часткову належність елемента x до нечіткої множина А.
означає часткову належність елемента x до нечіткої множина А.
На рис.3 представлена графічна ілюстрація функції належності змінної У, що показує на прикладі “Ціну”, для трьох нечітких значень („низька”, „середня”, „висока”).
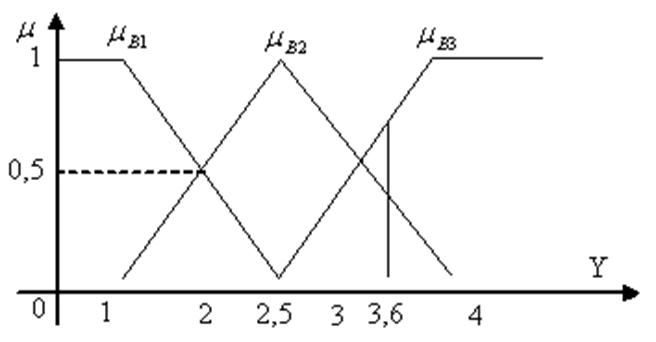
Рисунок 3 – Функції належності нечітких множин „низька” 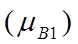 , „середня”
, „середня” 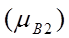 , „висока”
, „висока” 
 змінної “Ціна”.
змінної “Ціна”.
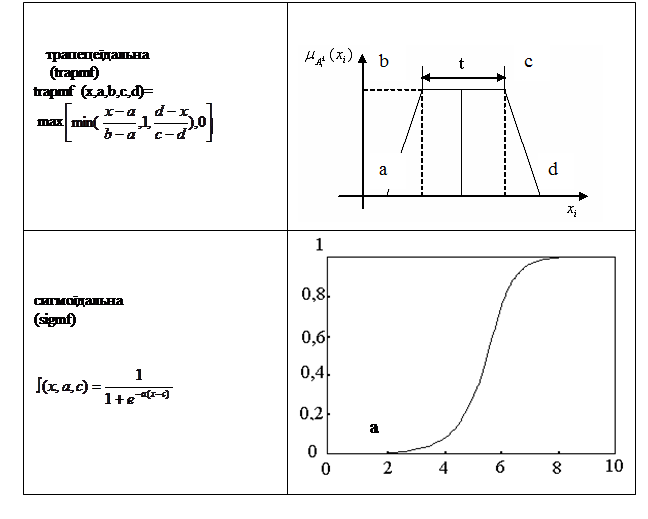
Для задання функції належності використовуються типові види функцій, представлені в таблиці 1 (вибирається та функція, яка найкращим чином апроксимує експертні оцінки).
Таблиця 1. – Типові види функцій, що використовується для задання функцій належності

|
|
|
|
|








|
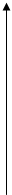









|
|
Визначення 2: Підмножина елементів S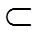 X, для яких
X, для яких 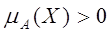 називається носієм (суппортом – анг. Support) нечіткої множини А і позначається наступним чином: Supp`A=
називається носієм (суппортом – анг. Support) нечіткої множини А і позначається наступним чином: Supp`A=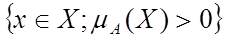 .
.
Визначення 3: Нечіткою змінною називається набір 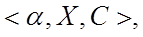 де
де 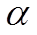 - найменування нечіткої змінної;
- найменування нечіткої змінної; 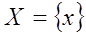 - область її визначення;
- область її визначення; 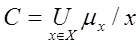 - нечітка множина на X, що описує обмеження на можливі значення нечіткої змінної
- нечітка множина на X, що описує обмеження на можливі значення нечіткої змінної 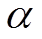 .
.
Згідно з визначенням Л.Заде, „під лінгвістичною змінною розуміється така змінна, значеннями якої є слова і словосполучення на деякій природній або штучній мові". Формально лінгвістичну змінну можна визначити таким чином:
Визначення 4. Лінгвістична змінна - це набір п'яти елементів: <Х, Т(Х), U, G, М>,
де Х- ім'я змінної; Т(Х) - множина термів, тобто множина імен (позначень) лінгвістичних значень Х; U - область міркувань (the universe of discourse); G - правило (the grammer) генерації імен; M - множина семантичних правил скріплення кожного Х з тим, що воно позначає. Наприклад, для опису вартості виробу в процесі прийняття рішень скористаємося такою лінгвістичною змінною: <Вартість,Т,[500, 1200],G,M>
де Т={МАЛА, НЕВЕЛИКА, СЕРЕДНЯ, ВЕЛИКА}; G-процедура вибору елементів множини Т; М - процедура експертного опитування.
Для розуміння основних логічних операцій над нечіткою множиною, що виконуються в процесі логічного нечіткого виведення введемо таке визначення.
Визначення 5: Трикутною Т-нормою називається функція двох змінних Т: 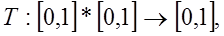 яка задовольняє таким умовам:
яка задовольняє таким умовам:
• Функція Т є монотонною незростаючою для двох змінних:
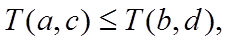 для
для 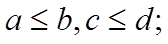
• Функція Т є обмеженою:
Т(а,0) = 0, Т(а, 1) = а, де а,b,с,d 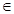 [0,1];
[0,1];
• Функція Т задовольняє умові асоціативності: Т(Т(а,b),с) = Т(а,Т(b,с));
• Функція Т задовольняє умові комутативності: Т(а,b)=Т(b,а).
Дію Т-норми на аргументах а і b позначаємо таким чином:
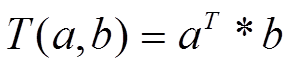 .
.
Частіше всього як функція Т використовуються такі вирази:
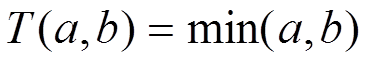
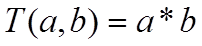 (добуток a,b)
(добуток a,b)
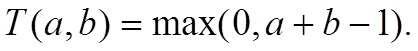
Якщо змінними а і b є функції належності нечіткої множини А і В, тоді можемо записати таку рівність:

де Т - є однією з вище представлених функцій.
Визначення 6: Трикутною S-нормою називається функція двох змінних S:
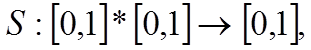 якщо є незростаючою і задовольняє таким умовам:
якщо є незростаючою і задовольняє таким умовам:
• комутативності: S(а,b) = S(b,а).
• асоціативності: S(S (а,b),с) - S(а,S(b,с));
• обмеженості - S(l, 1) = 1; S(а,0) = а; S(а, 1) =1;
Функція S називається також конормою або нормою дуальною відносно до Т-норми.
Дія S - норми на аргументах а і b позначаємо таким чином:
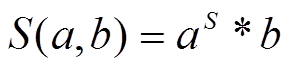
Приклади S-норми:
S(а,b) = max(а,b);
S(а,b)=а + b-а * b;
S(а,b) =min(1,а+b).
Якщо змінними а і b є функції належності нечіткої множини А і В, тоді суму цієї множини (об'єднання) можемо записати таким чином:
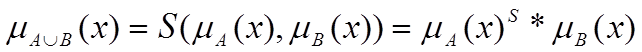
де S-норма є однією з вище представлених функцій.
Нечіткі відношення грають фундаментальну роль в теорії нечітких множин і логіки при моделюванні складних систем, оскільки із їх допомогою виконується операція нечіткого логічного виведенння. Подібно нечіткій множині, нечітке відношення можна задати за допомогою його функції належності:
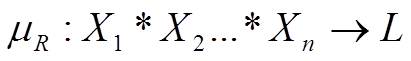
де L - може бути множиною дійсних чисел, відрізком [0,1] дійсної прямої, множиною лінгвістичних змінних або повною дистрибутивною граткою. Тоді під нечітким відношенням R розуміється функція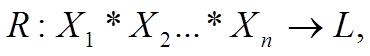 що відображує декартовий добуток множин
що відображує декартовий добуток множин 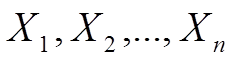 в L.
в L.
Визначення 7: Нечітким відношенням R між множинами Х і Y називається функція
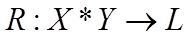
де в загальному випадку передбачається, що L - це повна дистрибутивна гратка.
Якщо нечіткі множини  і
і 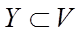 , задані на деякій універсальній множині:
, задані на деякій універсальній множині: 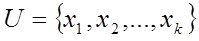 а
а 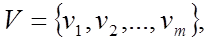 є складовими нечіткого правила „ЯКЩО Х, ТОДІ Y". Тоді нечітке відношення між множинами Х і Y представляють собою матрицю вигляду:
є складовими нечіткого правила „ЯКЩО Х, ТОДІ Y". Тоді нечітке відношення між множинами Х і Y представляють собою матрицю вигляду:
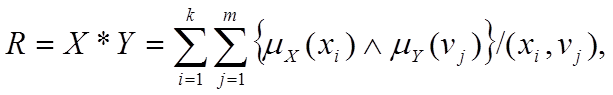
в якій елементи, розташовані на перетині i-того рядка і j-того стовпця визначаються таким чином:

Операція нечіткого логічного виведення має такий вигляд:
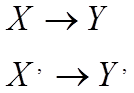
Такий запис інтерпретується таким чином:
ЯКЩО факт Х виходить з факту Y,ТО факт Х' виходить з Y',
де Х, Y, Х', Y' - нечіткі множини.
При цьому Y’ визначаємо за формулою:
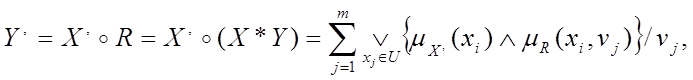
X,X’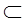 U,Y,Y’
U,Y,Y’ V
V
Визначення 8: Система нечіткого виведення представляє собою сукупність таких елементів:
 блок введення нечіткості (fuzzification);
блок введення нечіткості (fuzzification);
 другий блок – це основа системи – база нечітких знань, що формується спеціалістами предметної області у вигляді сукупності нечітких предикатних правил;
другий блок – це основа системи – база нечітких знань, що формується спеціалістами предметної області у вигляді сукупності нечітких предикатних правил;
 механізм логічних виводень рішень;
механізм логічних виводень рішень;
 блок приведення до чіткості (defuzzification).
блок приведення до чіткості (defuzzification).
Функціональна структура системи нечіткого виведення наведена на рис.4, яка в літературі називається системою Мамдані-Заде.
В блоці введення нечіткості виконується перетворення множини вхідних даних 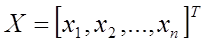 , в нечітку множину А, що характеризується функцією належності
, в нечітку множину А, що характеризується функцією належності 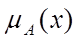 .
.

Рисунок 4 – Функціональна структура системи нечіткого виведення
Нечітка база знань представляє собою сукупність правил “ЯКЩО <входи> - ТОДІ <вихід>”, які відображають знання експерта і його розуміння причинно-наслідкових зв’язків, що характерні для об’єкта або процесу, які моделюються.
Нечітка база знань являє собою опис цих зв’язків на звичайній мові з використанням нечітких множин та лінгвістичних змінних.
Визначення 9: Нечітке узагальнене правило “ modus-ponens ” визначає така схема висновку:
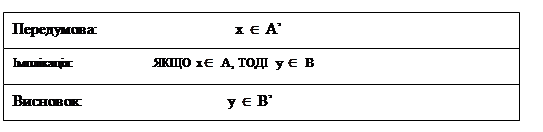
де 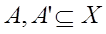 і
і 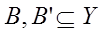 , є нечіткими множинами, визначеними на X,Y – які є непустими універсальними множинами, а x і y – лінгвістичні змінні. Тоді висновок нечіткого правила може бути записаний за допомогою нечіткої імплікації
, є нечіткими множинами, визначеними на X,Y – які є непустими універсальними множинами, а x і y – лінгвістичні змінні. Тоді висновок нечіткого правила може бути записаний за допомогою нечіткої імплікації 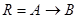 таким чином:
таким чином:
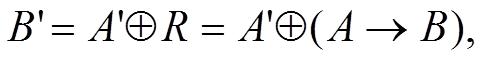
де “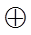 ” означає операцію композиції.
” означає операцію композиції.
Як було вище зазначено, нечітка імплікація рівносильна деякому нечіткому відношенню 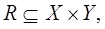 з функцією належності
з функцією належності 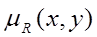 . Тому функцію належності нечіткої множини В’ можемо знайти за такою формулою:
. Тому функцію належності нечіткої множини В’ можемо знайти за такою формулою:
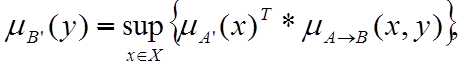
де 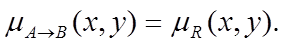 При цьому, в залежності від того яким чином реалізується Т-норма, формула може прийняти інший вигляд, тобто якщо Т-норма визначається як мінімум (min), тоді формула прийме такий вигляд:
При цьому, в залежності від того яким чином реалізується Т-норма, формула може прийняти інший вигляд, тобто якщо Т-норма визначається як мінімум (min), тоді формула прийме такий вигляд:
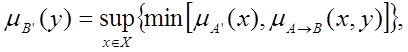
або виконується операція множення:
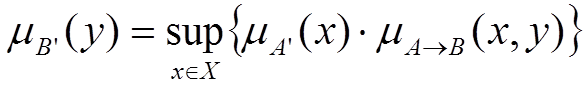
Крім представленого нечіткого правила висновку “modus-ponens” в нечіткій логіці використовується узагальнене нечітке правило “ modus-tollens ”.
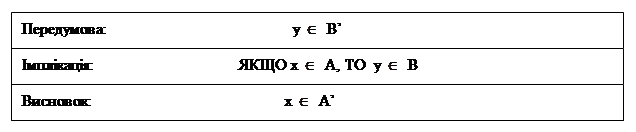
Визначення 10: Узагальнене нечітке правило “modus-tollens”визначає наступна схема висновку:
де 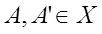 і
і 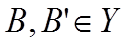 , є нечіткими множинами, визначеними на Х,У – які є непустими універсальними множинами, х і у – лінгвістичні змінні. Нечітка множина в схемі нечіткого висновку визначається в результаті композиції відношення:
, є нечіткими множинами, визначеними на Х,У – які є непустими універсальними множинами, х і у – лінгвістичні змінні. Нечітка множина в схемі нечіткого висновку визначається в результаті композиції відношення:
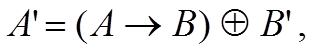
при цьому

Якщо Т-норма є типу min, тоді попередня формула прийме такий вигляд
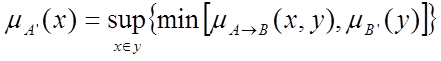
В даний час відомо багато різних методів нечіткої імплікації. Розглянемо найбільш відомі з них.
Методи визначення функції належності нечіткої імплікації
Нечітка імплікація типу 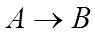 представляє собою набір правил, що визначають спосіб розрахунку функції належності нечіткого відношення
представляє собою набір правил, що визначають спосіб розрахунку функції належності нечіткого відношення 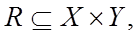 тобто
тобто
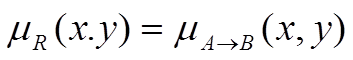
на основі відомих функцій належності 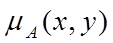 і
і 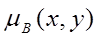 нечіткої множини
нечіткої множини 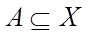 і
і 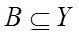 .
.
> Нечітка імплікація Mamdani:
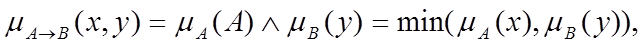
> Нечітка імплікація Zadeh:

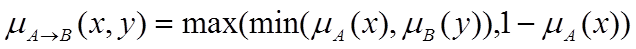
> Нечітка імплікація Larsena:
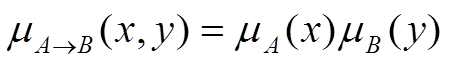
> Нечітка імплікація Kleene-Dienesa:
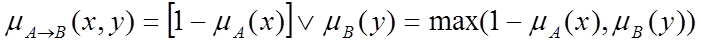
> Нечітка імплікація Lukasiewicza:
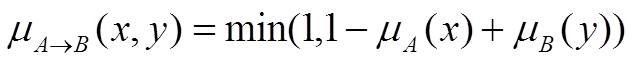
> Нечітка імплікація Yager'а:
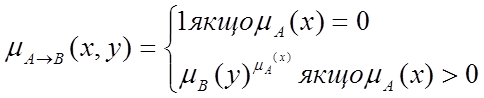
> Нечітка імплікація Willmott'а:
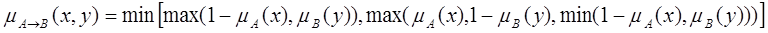
Методи приведення до чіткості
Трансформація нечіткої множини в єдине точкове рішення може бути виконана декількома відомими способами.
> Метод центру тяжіння області (Center of Area method = COА). Це найбільш широко використовуваний метод дефазифікації. Формула виглядає таким чином:
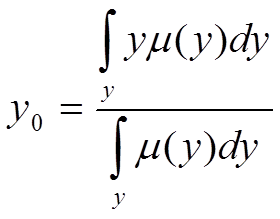
Спосіб визначення 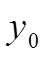 показаний на рисунку
показаний на рисунку
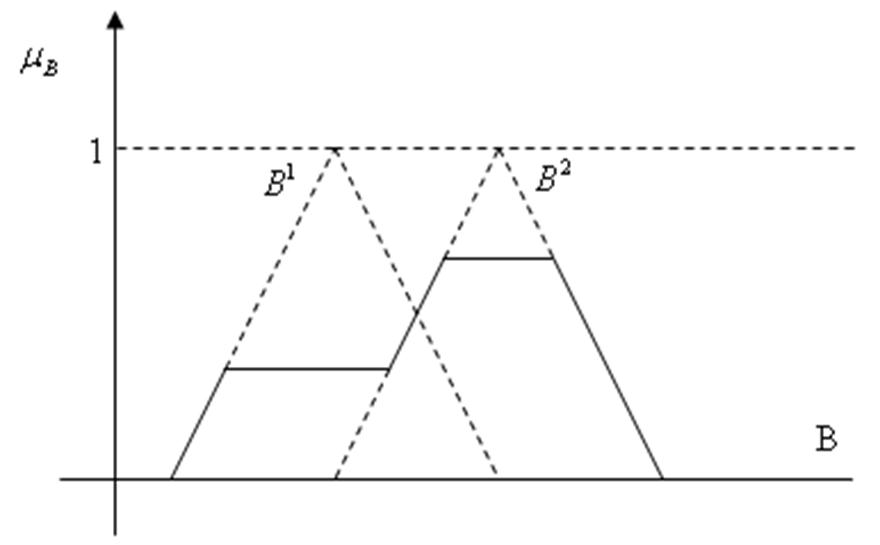
Рисунок 5 – Ілюстрація методу центра тяжіння області
В дискретному випадку розрахунок проводиться за формулою:

> Метод максимума критерію (max criterion method).
Суть цього методу полягає у виборі значення 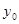 , при якому нечітка множина
, при якому нечітка множина 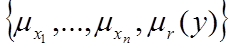 має максимальну ступінь належності:
має максимальну ступінь належності:
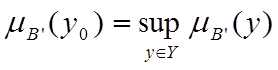
> Перший максимум (First-of-Maxima), Чітка величина висновку знаходиться як найменше значення, при якому досягається максимум кінцевої нечіткої множини:
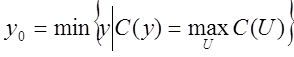
> Метод середнього центру (Center Average Defuzzyfication) визначає значення 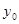 за такою формулою:
за такою формулою:
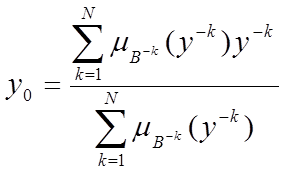
де 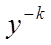 є точкою, в якій функція належності
є точкою, в якій функція належності 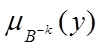 приймає максимальне значення
приймає максимальне значення
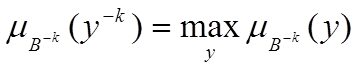
Точка 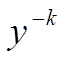 називається центром нечіткої множини
називається центром нечіткої множини 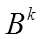 . На рисунку показана суть цього методу для N=2.
. На рисунку показана суть цього методу для N=2.
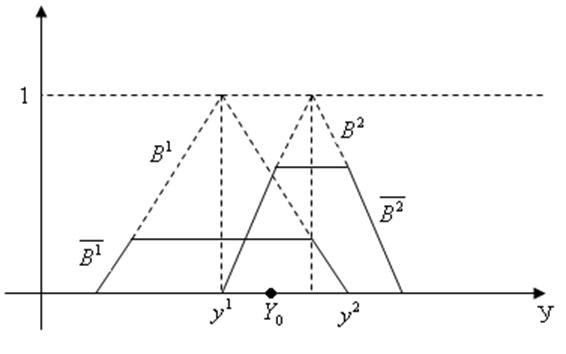
Рисунок 6 – Ілюстрація методу середнього центру
> Метод середнього значення максимуму (mean of maximum method=MOM)
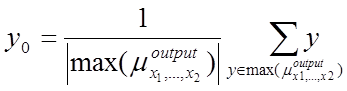
На практиці частіше всього застосовуються методи середнього центру.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 2972; Нарушение авторских прав?; Мы поможем в написании вашей работы!
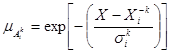
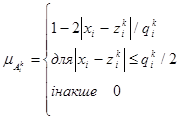
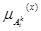 1
1
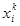
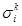
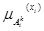 1
0
1
0