Блок-схеми алгоритмів

Наочною формою запису алгоритмів є блок-схеми, що складаються з геомет­ричних фігур - блоків. Кожний блок відповідає певній дії. Наприклад, запис алгоритму починається і закінчується такими блоками:

Ці елементи називаються блоками початку і кінця алгоритму. Стрілки вказують напрямок виконання алгоритму. Блок Початок має одну вихідну стрілку, а блок Кінець - одну вхідну стрілку.

У алгоритмах часто використовуються команди введення і виведення зна­чень. Цим командам відповідають блоки введення-виведення:

Тут лівий блок означає введення величини х, а правий блок - виведення у. За допомогою наведених вище блоків ви можете скласти найпростіший алгоритм введення величини х:

Відповідно до цього алгоритму в програму вводиться значення величини X. Однак програма, що складається тільки з операції введення, навряд чи доціль­на. Звичайно над введеною величиною виконуються певні дії, що позначаються прямокутними (операторними) блоками:

У середині прямокутників записані вирази, що виконуються над величинами. Лівий блок означає присвоювання змінній х значення суми х+1 (про операції присвоювання йтиметься в наступному параграфі). Правий блок відповідає за знаходження різниці х-у і надання значення різниці змінній z. Операторні блоки можуть мати кілька входів і лише один вихід.

Запишемо найпростіший алгоритм обчислення квадрата якогось числа:

Відповідно до цього алгоритму вводиться величина х, потім обчислюється квадрат цієї величини (добуток х*х) і виводиться отримане значення.

Усі наведені вище блоки дозволяють організувати послідовне виконання інструкцій алгоритму. Однак на практиці часто виникають ситуації, коли залежно від виконання будь-якої умови маємо змінити послідовний хід обчислень. Прикладом такої умови є нерівність 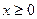в алгоритмі знаходження модуля числа х. У схему алгоритму логічна умова вводиться за допо­могою умовного блока. Цей блок прийнято зображати у вигляді ромба з одним входом і двома виходами:

Якщо умова, зазначена на зображенні блока, виконується (умова має зна­чення Істина), то відбувається перехід по стрілці Так, якщо не виконується (значення Хибність) - по стрілці Ні. Завдяки умовному блоку обчислювальний процес ніби розгалужується, тобто умовний блок використовується для ор­ганізації розгалуження.

Наведемо як приклад алгоритм обчислення модуля числа:

Запис цього алгоритму обмежують блоки початку і кінця. За блоком почат­ку алгоритму йде блок введення значень x, а за ним - умовний блок. В умовному блоці виконується перевірка умови 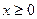і в результаті перевірки здійснюється перехід по одній із гілок Так або Ні. На кожній із гілок розташований операторний блок надання значень змінній y. Після операції надання гілки алгоритму сходяться, і наступна інструкція алгоритму міститься в блоці ви­ведення отриманого значення y.

Дата добавления: 2014-01-04