Аналіз табличних даних

Лекція 8. Фінансовий аналіз засобами табличного процесора Microsoft Excel

ЗАКЛЮЧЕННЯ

Правові основи охорони водних ресурсів України закладені у Законі про охорону навколишнього природного середовища (1991) та Водному кодексі України (1995), згідно з якими усі поверхневі і підземні води підлягають охороні від виснаження, забруднення, засмічення, замулення. Вирішенням питань охорони водних ресурсів України займаються Міністерство екології та природних ресурсів, Держкомітет України з гідрометеорології, Держкомітет України з водного господарства, Міністерство охорони здоров’я України.

Лекцію розробив:

Д.т.н., доцент М.І.Адаменко

Більшість менеджерів, що працюють у невеликих фірмах, не мають адекватних засобів автоматизації своєї роботи. Навіть якщо підприємство має корпоративну систему, то вона призначається як правило для оперативного управління. Тому для менеджерів-аналітиків, яким необхідно шукати оптимальні рішення, дуже актуальним є завдання автоматизації на основі «підручних» програмних засобів. В цій лекції буде показано, як можна розв’язувати задачі аналізу і прогнозу даних у табличному процесорі Excel, що входить у загальнодоступний пакет “Microsoft Office”.

Задача 1: Планування штатного розкладу

Авіакомпанії потрібно визначити, скільки стюардес слід прийняти на роботу протягом шести місяців при умові, що кожна з них повинна пройти попередню підготовку.

Потреби в кількості людино-годин літнього часу для стюардес відомі: в січні - 8000, в лютому - 9000, в березні - 8000, у квітні - 10000, в травні - 9000 і в червні - 12000.

Підготовка стюардеси до виконання своїх обов'язків займає один місяць. Отже, прийом на роботу повинен, по крайній мірі, на один місяць випереджати початок виконання нею обов'язків. Крім того, кожна стюардеса повинна протягом місяця, відведеного на її підготовку, пройти 100-годинну практику безпосередньо під час польотів. Таким чином, за рахунок кожної стюардеси, яка навчається, протягом місяця вивільнюється 100 людино-годин літнього часу, відведеного для вже навчених стюардес.

Кожна повністю навчена стюардеса протягом місяця може мати наліт до 150 годин. Авіакомпанія на початку січня вже має 60 досвічених стюардес. При цьому жодну з них не знімають з роботи. Встановлено також, що приблизно 10% стюардес, що навчаються, по закінченню навчання звільняються за різними обставинами.

Досвічена стюардеса обходиться авіакомпанії у 800$, а та, що навчається - в 400$ в місяць.

Необхідно спланувати штат авіакомпанії таким чином, щоб мінімізувати витрати за звітні шість місяців.

Розв'язування задачі:

1. Відведемо діапазон комірок В3:В8 під кількість нових стюардес, що приймаються на роботу з січня по червень.

2. В комірку В2 введемо кількість стюардес, що працюють у грудні.

3. В діапазоні комірок D3:D8 обчислимо кількість стюардес, які постійно працюють у поточному місяці, шляхом введення у комірки D3 і D4 формул:

D3 =В2

D4 =D3+0,9*B3

і протягуючи останню з них на діапазон D5:D8.

4. В діапазоні Е3:Е8 обчислимо наліт помісячно, вводячи в комірку Е3 формулу:

Е3 =D3*$G$12+B3*$F$12

і протягуючи її на діапазон Е4:Е8, де в комірки F12 і G12 введені допустимий наліт стюардес, що навчаються та працюють.

5. В діапазоні F3:F8 обчислимо витрати помісячно, вводячи в комірку F3 формулу:

F3 =D3*$E$12+B3*$D$12

і протягуючи її на діапазон F3:F8, де в комірки D12 і Е12 введені витрати на навчання і роботу стюардеси.

6. Обчислимо сумарні витрати на плановий період в комірці F9 за формулою:

F9 =СУММ(F3:F8)

7. Сервис - Поиск решения.

Цільова функція: в комірці F9

Змінні моделі: в діапазоні В3:В8

Обмеження: В3:В8=целое

В3:В8>=0

E3:E8>=C3:C8

Задача 2: Задача про призначення

Четверо робітників можуть виконувати чотири види робіт. Вартості с_ij виконання i-м робітником j-ї роботи наведені в комірках діапазону A1:D4. В таблиці рядки відповідають робочим, а стовпці - роботам.

Необхідно скласти план виконання робіт так, щоб всі роботи були виконані, кожен робітник був завантажений лише на одній роботі, а сумарна вартість виконання всіх робіт була мінімальною.

Відмітимо, що така задача є збалансованю, тобто кількість робіт співпадає з кількістю робітників. Якщо задача не збалансована, то перед початком розв'язування її необхідно збалансувати, ввівши недостатню кількість фіктивних рядків або стовпців із достатньо великими штрафними вартостями робіт.

Розв'язування задачі:

Для розв’язування цієї задачі побудуємо її математичну модель. Нехай змінна х_ij =1, якщо i-м робітником виконується j-та робота, і х_{i j}=0, якщо i -м робітником не виконується j-та робота.

Тоді модель має наступний вигляд:

Мінімізувати

при обмеженнях:

Для розв’язування цієї задачі за допомогою засобу «Пошук розв’язку» відведемо під невідомі діапазон комірок F2:I5.

1. В комірку K1 введемо цільову функцію = СУММПРОИЗВ (G2:J5; B2:E5), яка обчислює вартість робіт.

2. Введемо формули, що задають ліві частини обмежень:

В комірку G6: =CУММ (G2:G5) і протягнути її на діапазон комірок H6:J6.

В комірку K2: =CУММ (G2:J2) і протягнути її на діапазон комірок K3:K5.

3. Викликати діалогове вікно «Пошук розв’язку».

4. Ввести обмеження:

G2:J5<=1

G2:J5=целое

G2:J5>=0

G6:J6=1

K2:K5=1

Задача 3. Транспортна задача

Фірма має 4 фабрики і 5 центрів розподілу її товарів.

Фабрики фірми знаходяться в Денвері, Бостоні, Новому Орлеані і Далласі з виробничими можливостями 200, 150, 225 і 175 одиниць продукції щоденно, відповідно.

Центри розподілу товарів фірми розміщуються в Лос-Анджелесі, Далласі, Сент-Луїсі, Вашингтоні і Атланті з потребами в 100, 200, 50, 250 і 150 одиниць продукції щоденно, відповідно.

Зберігання на фабриці одиниці продукції, не доставленої до центру розподілу, обходиться в $ 0,75 в день, а штраф за невчасну поставку одиниці продукції, замовленої споживачем в центрі розподілу, але яка там не знаходиться, рівний $ 2,5 в день.

Вартість перевезення одиниці продукції з фабрик до пунктів розподілу наведена "Транспортні витрати".

Необхідно так спланувати перевезення, щоб мінімізувати витрати.

	Лос-Анджелес	Даллас	Сент-Луіс	Вашингтон	Атланта
Денвер	1,5		1,75	2,25	2,25
Бостон	2,5		1,75		1,5
Новий Орлеан		1,5	1,5	1,75	1,75
Даллас		0,5	1,75	1,75	1,75

Оскільки дана модель збалансована (сумарний об’єм виготовленої продукції рівний сумарному об’єму потреб продукції), то в цій моделі не слід враховувати витрати, пов’язані як із залишками продукції на складах, так і з недостатніми поставками продукції.

В протилежному випадку до моделі потрібно було б ввести:

1. У випадку надвиробництва – фіктивний пункт розподілу, в який вартість перевезень одиниці продукції був би рівним вартості складирования, а об’єми перевезень – об’ємам накопичення надлишків продукції на фабриках.

2. У випадку дефіциту – фіктивну фабрику, вартість перевезень продукції з якої вважається рівною вартості штрафів за недостатню поставку продукції, а об’єми перевезень – об’ємам недостатньої кількості поставок до пунктів розподілу.

Розв’язування.

Для розв’язування побудуємо математичну модель задачі.

Невідомими даної задачі є об’єми перевезень. Нехай х_ij – об’єм перевезень з і-ї фабрики до j-го центру розподілу. Цільова функція – це сумарні транспортні витрати, тобто

де c_ij – вартість перевезення одиниці продукції з з і-ї фабрики до j-го центру розподілу.

Невідомі даної задачі повинні задовольняти наступним обмеженням:

1. Об’єми перевезень не можуть бути від’ємними;

2. Оскільки модель збалансована, то вся продукція повинна бути вивезена з фабрик, а потреби всіх центрів розподілу повинні бути задоволені в повній мірі.

В результаті матимемо наступну модель:

Мінімізувати

при обмеженнях:

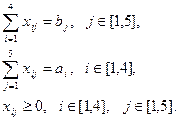
де а_ij – об’єм виробництва на і-й фабриці, b_j – попит в j-му центрі розподілу.

Для розв’язування за допомогою пошуку розв’язку введемо дані в комірки електроноої таблиці.

В комірки B2:F5 введені вартості перевезень. Комірки B8:F11 відведені для значень невідомих (об’єми перевеезнь). В комірки Н8:Н11 ввести об’єми виробництва на фабриках, а в комірки B13:F13 ввести потреби продукції в пунктах розподілу. В комірку G12 ввести цільову функцію

=СУММПРОИЗВ (B2:F5; B8:F11)

В комірку В12 ввести формулу для обчислення сумарного об’єму продукції, яка ввозиться до центру розподілу в Лос-Анджелесі за формулою =СУММ (В8:В11) і протягнути її на комірки C12:F12.

В комірку G8 ввести формулу для обчислення сумарного об’єму продукції, яка вивозиться з фабрики в Денвері за формулою =СУММ (В8:F8) і протягнути її на комірки G9:G11.

Далі слід викликати засіб Пошук розв’язку та заповнити даними діалогове вікно.

Обмеження:

B12:F12 = B13:F13

G8:G11 = H8:H11

B8:F11>=0

Дата добавления: 2014-01-04