Лекція №14. Визначення графа як абстрактного математичного поняття

Контрольні запитання

1. Які фактори впливають на розміщення снігової лінії?
2. Дайте визначення поняттю лавина, які існують їхні різновидності і де вони виникають?
3. Яким чином відбувається перетворення снігу в глетчерний лід та утворення льодовика?
4. Охарактеризуйте роботу льодовиків.
5. Що таке абляція та яких видів вона буває?
6. Від яких факторів залежить характер зміни об’єму і форми льодовика?
7. Чим обумовлений рух льодовиків?
8. На які типи поділяються льодовики і де вони поширені?
9. Яку роль відіграють льодовики у гідрологічному режимі річок?
10. Охарактеризуйте господарське значення льодовиків.

Ключові термінологічні поняття: снігова лінія, лавина, льодовик, фірн, глетчерний лід, режеляція, морени, абляція, материкові та гірські льодовики, айсберг.

Визначення (p,q) графа, (1,0) графа

Ізоморфність графів

Поняття підграфа і надграфа

Маршрут, ланцюг, цикл в графі

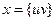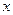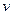Граф складається з скінченої непустої множини , яка містить вершин і заданої множини , яка має невпорядкованих пар різних вершин з . Будь-яку пару вершин в називають ребром графа і говорять, що з’єднує вершину з вершиною . Будемо писати 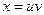і говорити, що і 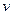суміжні вершини; вершина і ребро 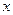інцидентні. Якщо два різних ребра 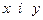інцидентні одній і тій самій вершині, то вони називаються суміжними. Граф з вершинами і ребрами називається -графом. 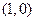граф називається тривіальним. Граф з даними ребрами є деяка підмножина добутку 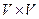. Якщо для ребра 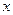виконується умова , то 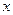неорієнтоване ребро, якщо ж порядок існує, то ребро називається орієнтованим. Орієнтовані ребра позначаються стрілкою.

Граф називається неорієнтованим, якщо неорієнтоване будь-яке ребро графа і орієнтованим, якщо орієнтовані усі його ребра. Змішані графи мають як орієнтовані так і неорієнтовані ребра.

Для будь-якого орієнтованого графа існує обернений граф 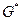, який одержується зміною орієнтації ребер на протилежну.

Для будь-якого орієнтованого графа існує співвіднесений неорієнтований граф 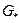, ребрами якого являються ребра графа , але вже без орієнтації.

Неорієнтований граф можна перетворити в орієнтований за допомогою операції подвоєння, суть якої полягає в тому, що усі ребра графа замінюються парою ребер протилежної орієнтації.

Граф називається плоским, якщо він може бути зображений на площині так, що усі перетини його ребер являються вершинами .

Петля – це ребро, яке з’єднує вершину саму з собою. В мультиграфі не допускаються петлі, але пари вершин можуть з’єднуватися більш ніж одним ребром. Ці ребра називаються кратними. Якщо допускаються петлі та кратні ребра одержуємо псевдограф.

Граф називається поміченим (занумерованим), якщо його вершини відрізняються одна від одної якимись помітками.

Два графа і і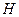зоморфні, якщо між їх множинами вершин існує взаємно-однозначна відповідність, яка зберігає суміжність. Очевидно, ізоморфізм є відношенням еквівалентності на графах.

Вершина, яка не інцидентна жодному ребру називається ізольованою. Граф, який складається тільки з ізольованих вершин називається нуль-графом.

Повний граф – це граф, у якому ребра - це усі можливі пари вершин.

Інваріант графа - це число, яке пов’язане з і яке приймає одне і те саме значення на будь-якому графі, ізоморфному . Числа і називаються інваріантами графа.

Підграфом графа називається граф, у якого усі вершини і ребра належать графу . Якщо 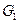- підгаф графа , то називається надграфом графа .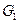

Остовний підграф – це підграф , який містить усі вершини графа .

Для будь-якої підмножини 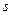вершин графа породженим підграфом 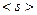називається максимальний підграф графа , множиною вершин якого являється 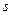. Таким чином, дві вершини з 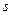суміжні тоді і тільки тоді, коли вони суміжні в .

: :

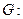
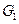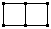
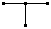
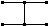
породжений, остовний, але

але не остовний не породжений

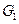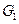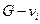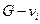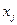Підграфи і не перетинаються (по вершинам), якщо вони не мають спільних вершин, а отже і спільних ребер. Якщо і не перетинаються, то їх сума називається прямою. Вилучення вершини з графа приводить до підграфа , який містить усі вершини графа , за виключенням вершини, і усі ребра графа , які не інцидентні вершині . Іншими словами, є максимальний підграф графа . Вилучення ребра з приводить до остовного підграфа, який містить усі ребра графа за виключенням 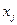, тобто є максимальним підграфом , який не містить . 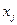Вилучення довільної множини вершин або ребер з визначається як послідовне вилучення усіх елементів цієї множини. Якщо і 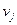не суміжні в , то долучення ребра утворює найменший надграф графа , який містить ребро .

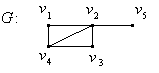
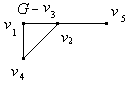
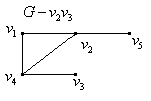
Маршрут - це послідовність вершин і ребер 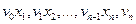. Ця послідовність починається і закінчується вершиною, 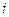будь-яке ребро послідовності інцидентне двом вершинам, одна з яких безпосередньо передує йому, а друга безпосередньо слідує за ним. Вказаний маршрут з’єднує вершини і і його можна позначити . Маршрут називається замкненим, якщо 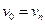і відкритим у противному разі. Маршрут називається ланцюгом, якщо усі його ребра різні, простим ланцюгом, якщо всі його вершини (а отже, і ребра) різні. Замкнений ланцюг називається циклом. Замкнений маршрут називається простим циклом, якщо усі його 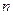-вершини різні. Маршрут нетривіальний, якщо він містить хоча б одне ребро. Нуль - маршрут не містить жодного ребра.

Наприклад:

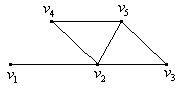
- не ланцюг

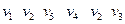- це ланцюг, але не простий

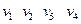- простий ланцюг

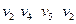- простий цикл

Нехай - неорієнтований граф. Дві вершини і 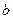називаються зв’язаними, якщо існує маршрут з кінцями і 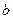. Якщо маршрут проходить через деяку вершину 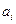більше одного разу, то можна вилучити його циклічну частину. З цього слідує, що зв’язані маршрутом вершини зв’язані також простим ланцюгом.

Граф називається зв’язаним, якщо будь-яка його пара вершин зв'язана.

Теорема 1.1 Будь-який неорієнтований граф розкладається єдиним чином в пряму суму своїх зв’язних компонент.

Доведення:

Для зв’язаних вершин і 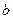виконується відношення еквівалентності. Але усі вершини, які зв’язані з або 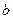також знаходяться у відношенні еквівалентності і утворюють клас еквівалентності (тобто це підмножина зв’язаних вершин). Два різних класи еквівалентності не можуть мати спільної вершини, в противному разі вони б співпадали, що слідує з властивостей відношення еквівалентності. Таким чином, існує такий розклад множини вершин 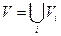на підмножини, що попарно не перетинаються, що усі вершини в кожному зв’язані, а вершини з різних не зв’язані. Отже, можна записати розклад: 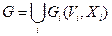графа 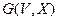на підграфи 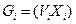. Внаслідок попарного неперетину підграфів розклад називається прямим, а самі підграфи називаються компонентами зв’язності графа .

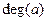Граф називається скінченим, якщо кількість його ребер скінчена. Скінчений граф може мати нескінчене число вершин, але всі вони, окрім скінченого числа, ізольовані. Нехай - неорієнтований граф. Число ребер інцидентних одній вершині будемо позначати . Це число називається степенем графа в вершині . Нехай число ребер в графі . Оскільки кожне ребро враховується в двох ступенях 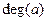(в і в 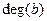), то сума усіх ступенів графа .

Теорема 1.2 В скінченому графі число вершин непарного ступеню парне.

Доведення:

Маємо 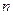вершин .

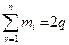. Оскільки сума парних ступенів число парне, а в правій частині рівності знаходиться парне число 2, то число непарних ступенів повинно бути парним.

Граф називається однорідним ступеня 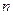(або регулярним), якщо всі його ступені у всіх його вершинах дорівнюють .

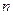Наприклад:

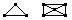
Отже, в однорідному графі ступеня 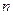, який має 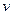вершин, кількість ребер 2.

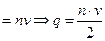Дата добавления: 2014-01-04