
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекція №17. Операції над графами
|
|
|
|
Питання для самоперевірки та вправи
1. Які ви знаєте способи машинного представлення графа? В яких випадках доцільно використовувати кожний спосіб?
2. Намалюйте довільний граф, позначте його вершини і ребра. Дайте матричну інтерпретацію цього графа.
3. Дайте машинну інтерпретацію графа, створеного в пункті 2. Обгрунтуйте вибраний спосіб.
4. Створіть схему з полем зв'язків для графа, створеного в пункті 2.
Об’єднання, переріз, сума та різниця графів
Декартовий добуток графів
Композиція графів
Нехай 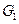 і
і  - два орієнтованих графа, множини
- два орієнтованих графа, множини  вершин і множини
вершин і множини 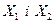 ребер цих графів не перетинаються.
ребер цих графів не перетинаються.
Об’єднанням графів 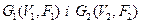 називається граф
називається граф  , вершинами якого є множина
, вершинами якого є множина  , а відображення
, а відображення 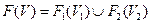 .
.
Наприклад:
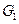 : :
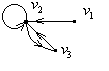

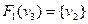
|  : :
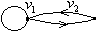

|
Тоді об’єднанням графів  буде граф:
буде граф:
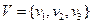
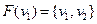
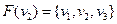
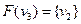
| 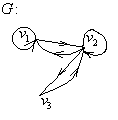
|
Перерізом графів 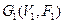 і
і 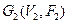 називається граф
називається граф 
 , для якого виконуються умови
, для якого виконуються умови  ,
, 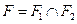 .
.
Наприклад:
Розглянемо переріз графів, зображених у попередніх прикладах:


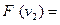

Одержимо граф 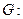
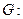
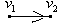
Різницею графів 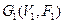 і
і 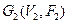 називається граф
називається граф 
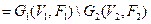 , для якого виконуються умови
, для якого виконуються умови 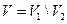 ,
, 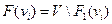 , тобто, якщо, наприклад, множина вершин деякого графа
, тобто, якщо, наприклад, множина вершин деякого графа 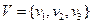 і
і  , то
, то 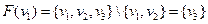 .
.
Різниця графів, розглянутих у попередніх прикладах буде: 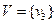 ,
,  . Одержимо:
. Одержимо: 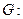
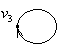
Композиція графів 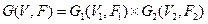 визначається по таким правилам:
визначається по таким правилам:
1. Вершинами результуючого графа є множина  .
.
2. Відображення кожної вершини визначається 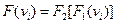 .
.
Наприклад:
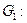

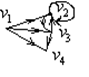

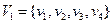

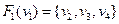
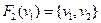




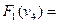

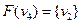
Створимо граф  , як композицію графів
, як композицію графів  :
:



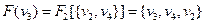
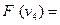

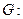
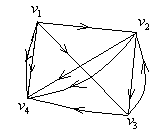
Побудова декартового добутку 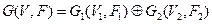 визначається таким правилом:
визначається таким правилом:
1. Вершини графа  одержуємо шляхом послідовного сполучення кожної з вершин першого графа
одержуємо шляхом послідовного сполучення кожної з вершин першого графа 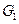 з кожною з вершин другого графа
з кожною з вершин другого графа  . Отже, в графі
. Отже, в графі  кожна вершина має двохзначне позначення. Загальна кількість вершин графа
кожна вершина має двохзначне позначення. Загальна кількість вершин графа  дорівнює добутку вершин графів
дорівнює добутку вершин графів  , так, наприклад, якщо маємо множини вершин
, так, наприклад, якщо маємо множини вершин  ,
,  , тоді
, тоді 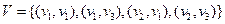 .
.
2. Відображення кожної вершини в декартовому добутку графів 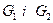 одержуємо шляхом можливих сполучень кожного з відображень графа
одержуємо шляхом можливих сполучень кожного з відображень графа 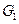 з кожним з відображень графа
з кожним з відображень графа  для відповідних вершин. Загальна кількість відображень для кожної вершини графа
для відповідних вершин. Загальна кількість відображень для кожної вершини графа  дорівнює добутку числа відображень графів
дорівнює добутку числа відображень графів 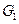 та
та  для відповідних вершин, тобто
для відповідних вершин, тобто
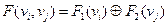
Наприклад:
Визначити відображення для вершини , якщо відомо
, якщо відомо 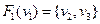 ,
, 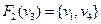
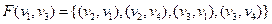 .
.
Розглянемо приклад:
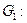 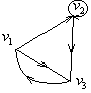
|  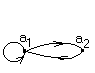
|
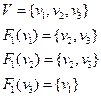
|
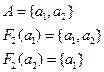
|

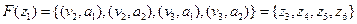

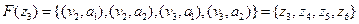
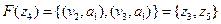
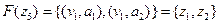
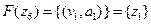
Сумою графів 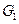 і
і  називається граф
називається граф 
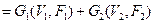 , який визначається по таким правилам:
, який визначається по таким правилам:
1. Вершини графа  визначаються аналогічно декартовому добутку
визначаються аналогічно декартовому добутку  .
.
2. Відображення для будь-якої вершини 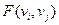 графа
графа  одержують шляхом об’єднання двох сполучень, одне з яких одержане відображенням вершини
одержують шляхом об’єднання двох сполучень, одне з яких одержане відображенням вершини  графа
графа 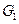 і вершиною
і вершиною 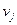 графа
графа  , а друге - вершиною
, а друге - вершиною  графа
графа 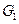 і відображенням вершини
і відображенням вершини 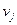 графа
графа  :
: 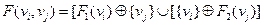 .
.
Наприклад:
Треба визначити образ  , якщо виконуються умови
, якщо виконуються умови  ,
,  . Визначимо можливі сполучення
. Визначимо можливі сполучення  з
з 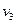 і
і 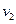 з
з  .
.


Для прикладу визначимо суму графів які розглядались для визначення їх декартового добутку:

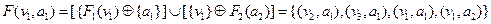
 .
.
Подальшу побудову графа  пропонуємо читачеві.
пропонуємо читачеві.
Операції над неорієнтованими графами
Розглянемо операції над графами  і
і  , які мають множини вершин
, які мають множини вершин 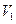 і
і  і множини ребер
і множини ребер  і
і 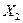 , які не перетинаються. Тоді визначені такі операції:
, які не перетинаються. Тоді визначені такі операції:
| Операція | Число вершин | Число ребер |
Об’єднання 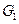 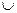 
| 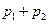
| 
|
З’єднання 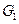 + +
| 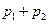
| 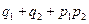
|
Добуток 
| 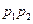
| 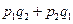
|
Композиція
| 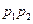
| 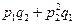
|
Наприклад: Об’єднання:

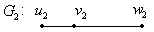
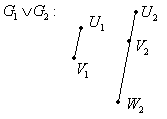
З’єднання: Добуток:
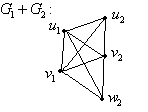
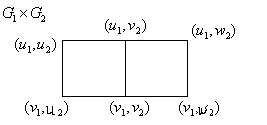
Вершини  і
і 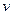 суміжні в
суміжні в  тоді і тільки тоді, коли
тоді і тільки тоді, коли 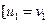 і
і 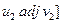 або
або  .
.
Композиція:


Вершина 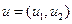 суміжна з
суміжна з  тоді і тільки тоді, коли
тоді і тільки тоді, коли  або
або 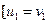 і
і 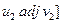 .
.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 3392; Нарушение авторских прав?; Мы поможем в написании вашей работы!