Случайные процессы с независимыми приращениями

Стационарные случайные процессы.

Понятие случайного процесса. Характеристики случайных процессов.

Лекция 18

Определение. Случайным процессом называется семейство случайных величин 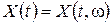, заданных на вероятностном пространств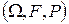е , где 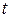есть текущее время. Множество 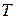значений параметра 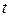называют областью определения случайного процесса, а множество 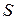возможных значений 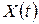– пространством значений случайного процесса.

Случайный процесс, в отличие от детерминированного процесса, заранее предсказать невозможно. В качестве примеров случайных процессов можно рассмотреть броуновское движение частиц, работу телефонных станций, помехи в радиотехнических системах и т. д.

Если область определения 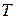случайного процесса представляет конечное или счетное множество отсчетов времени, то говорят, что 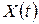– случайный процесс с дискретным временем или случайная последовательность (цепь), а если область определения 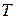– континуум, то 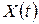называют случайным процессом с непрерывным временем.

В том случае, когда пространство 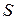значений случайного процесса является конечным или счетным множеством, то случайный процесс называют дискретным. Если же пространство 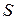значений случайного процесса – континуум, то случайный процесс называют непрерывным.

Действительную функцию 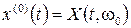при некотором фиксированном значении 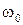называют реализацией или траекторией случайного процесса. Таким образом, случайный процесс представляет собой совокупность всевозможных своих реализаций, то есть 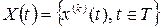, где индикатор реализаций 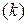может принадлежать счетному множеству действительных чисел или континууму. Детерминированный же процесс имеет единственную реализацию, описываемую заданной функцией .

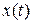При фиксированном 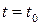получаем обычную случайную величину 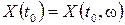, которая называется сечением случайного процесса в момент времени .

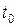Одномерной функцией распределения случайного процесса 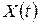при фиксированном 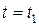называется функция

, .

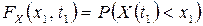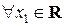Эта функция задает вероятность множества траекторий, которые при фиксированном 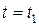проходят ниже точки .

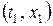При 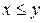из определения (5.1.1) одномерной функции распределения следует, что равенство 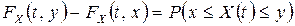задает вероятность множества траекторий, проходящих через «ворота» между точкам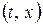и и .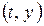

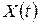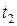Двумерной функцией распределения случайного процесса при фиксированных и называется функция

, .

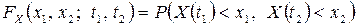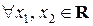Эта функция задает вероятность множества траекторий, которые одновременно проходят ниже точек 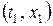и .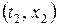

Аналогично 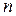- мерная функция распределения случайного процесса 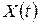при фиксированных 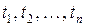определяется равенством

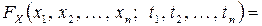
для всех из .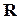

Если эта функция достаточное число раз дифференцируема, то 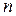- мерная совместная плотность вероятности случайного процесса 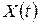имеет вид

.

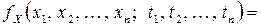
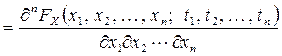Функция распределения или плотность вероятности тем полнее описывает сам случайный процесс, чем больше 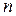. Эти функции учитывают связь хотя и между любыми, но лишь фиксированными сечениями этого процесса. Случайный процесс считается заданным, если задано множество всех его 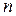- мерных законов распределения или 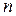- мерных плотностей вероятности для любых 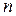. При этом функция распределения должна удовлетворять условиям симметрии и согласованности Колмогорова. Условие симметрии состоит в том, что 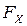– симметричная функция для всех пар 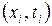, , 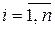в том смысле, что, например,

.

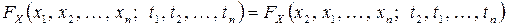Условие же согласованности означает, что

,

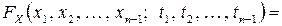
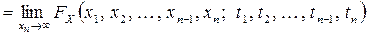то есть 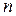- мерный закон распределения случайного процесса 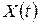определяет все законы распределения более низкой размерности.

Рассмотрим различные характеристики случайных процессов.

Определение. Математическим ожиданием или средним значением случайного процесса 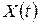называется функция

,

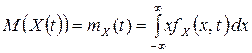где – одномерная плотность вероятности случайного процесса. Геометрически математическому ожиданию соответствует некоторая кривая, около которой группируются траектории случайного процесса.

Определение. Дисперсией случайного процесса 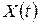называется функция

.

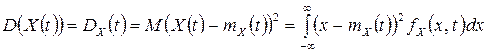Таким образом, математическое ожидание и дисперсия случайного процесса 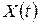зависят от одномерной плотности вероятности и являются неслучайными функциями времени 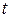. Дисперсия случайного процесса характеризует степень разброса траекторий относительно его среднего значения 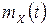. Чем больше дисперсия, тем значительнее разброс траекторий. Если дисперсия равна нулю, то все траектории случайного процесса 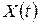совпадают с математическим ожиданием 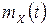, а сам процесс является детерминированным.

Определение. Корреляционная функция 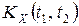случайного процесса 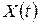определяется равенством

,

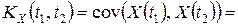
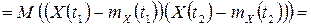
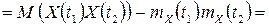
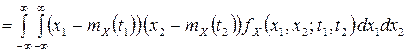где 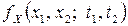– двумерная плотность вероятности случайного процесса.

Корреляционная функция 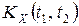характеризует степень связи между ординатами случайного процесса 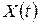для двух моментов времени и 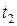. При этом, чем больше корреляционная функция, тем более гладкими являются траектории случайного процесса 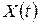, и наоборот.

Корреляционная функция обладает следующими свойствами.

1⁰. Симметричность: , .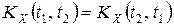

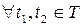2⁰. , .

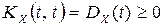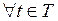Эти свойства следуют из соответствующих свойств ковариации случайной величины.

Теория, изучающая случайные процессы на основе математического ожидания и корреляционной функции, называется корреляционной теорией. С помощью методов корреляционной теории исследуются в основном линейные системы автоматического регулирования и управления.

Определение. Случайный процесс 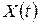, , 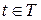называется стационарным в узком смысле, если совместное распределение случайных величин

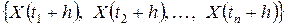и ,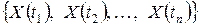

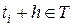
одинаково и не зависит от 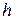, то есть

.

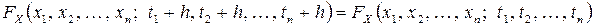Отсюда для 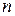- мерной плотности вероятности справедливо соотношение

.

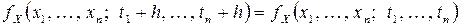Учитывая, что 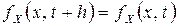в случае одномерной плотности вероятности, и полагая в этом соотношении 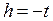, имеем 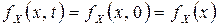. Отсюда для стационарного случайного процесса находим следующее выражение для математического ожидания:

.

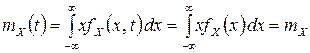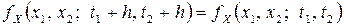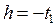Аналогично для двумерной плотности вероятности из равенства при получим 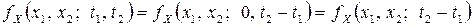. Следовательно, корреляционную функцию можно записать в виде

,

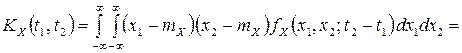
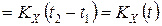где .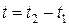

Таким образом, для стационарных случайных процессов в узком смысле, математическое ожидание есть постоянная величина, а корреляционная функция зависит только от разности аргументов, то есть 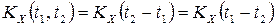, так как корреляционная функция симметрична.

Определение. Случайный процесс с постоянным математическим ожиданием и корреляционной функцией, зависящей только от разности аргументов, называется случайным процессом, стационарным в широком смысле. Ясно, что стационарный в узком смысле случайный процесс является стационарным и в широком смысле. Обратное же утверждение в общем случае неверно.

Корреляционная функция стационарного случайного процесса обладает приведенными ниже свойствами.

1⁰. 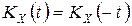, то есть функция 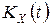– четная.

2⁰. Справедливо неравенство .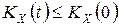

3⁰. Для дисперсии стационарного случайного процесса 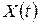справедливо соотношение .

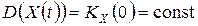Пусть 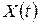, , 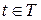– стационарный случайный процесс, непрерывный по времени 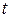, с математическим ожиданием 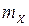и корреляционной функцией .

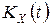Определение. Функция, обозначаемая 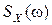и определяемая соотношением

,

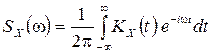называется спектральной плотностью.

Если известна спектральная плотность 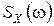, то с помощью преобразования Фурье можно найти корреляционную функцию

.

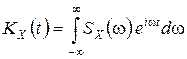Последние два равенства называются формулами Винера – Хинчина.

Очевидно, что для существования обратного преобразования Фурье достаточно существования интеграла 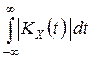, то есть достаточно абсолютной интегрируемости на промежутке 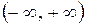корреляционной функции .

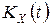Можно показать, что спектральная плотность 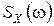стационарного случайного процесса является четной функцией, то есть .

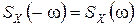Так как 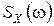– четная функция, то

,

.

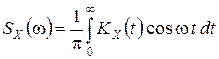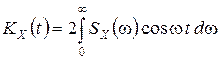Из этих формул и определения корреляционной функции 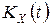следует, что дисперсия стационарного случайного процесс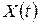а равна

.

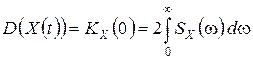Если случайный процесс есть флуктуация электрического тока или напряжения, то дисперсия случайного процесса как среднее значение квадрата тока или напряжения пропорциональна средней мощности этого процесса. Поэтому из последнего равенства следует, что спектральная плотность 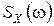в этом случае характеризует плотность мощности, приходящуюся на единицу круговой частоты .

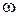На практике вместо спектральной плотности 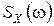часто применяют нормированную спектральную плотность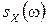, равную

.

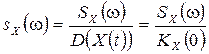Тогда, как нетрудно убедиться, так называемая нормированная корреляционная функция 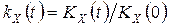и нормированная спектральная плотность 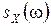связаны прямым и обратным преобразованиями Фурье:

, .

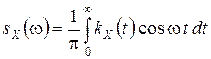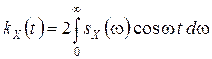Полагая 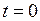и учитывая, что 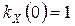, имеем

.

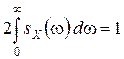Учитывая четность спектральной функции, получаем

,

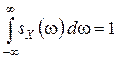то есть полная площадь, ограниченная снизу осью 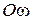и сверху графиком нормированной спектральной плотности, равна единице.

Определение. Случайный процесс 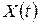, , 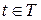называется процессом с независимыми приращениями, если для любых 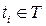, , 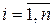, 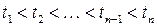случайные величины

, , …,

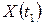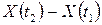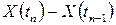
независимы.

В этом случае для различных пар случайных величин корреляционная функция равна нулю.

Если случайные величины попарно некоррелированы, то случайный процесс 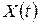называется процессом с некоррелированными или ортогональными приращениями.

Так как случайные величины независимы, то они некоррелированы (ортогональны). Тем самым всякий процесс с независимыми приращениями есть процесс с ортогональными приращениями.

Пусть 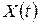– случайный процесс с ортогональными приращениями. Тогда для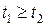 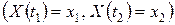получаем

,

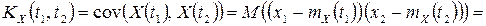
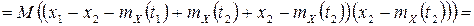
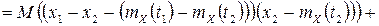
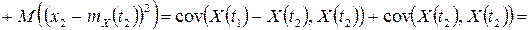
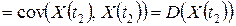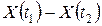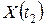поскольку случайные величины и ортогональны.

Аналогично при 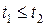получим, что .

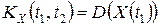Таким образом, корреляционная функция 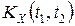случайного процесса с ортогональными приращениями обладает свойством

.

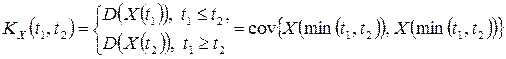Применяя функцию Хевисайда 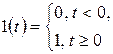, корреляционную функцию можно записать в виде

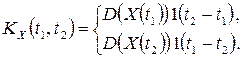
Дата добавления: 2014-01-04