Зоны Френеля

Как следует из принципа Гюйгенса- Френеля комплексная амплитуда волны в точке наблюдения 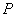(рис. 5.4), создаваемая источником монохроматической электромагнитной волны в точке 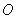, может быть найдена как суперпозиция комплексных амплитуд сферических волн, испускаемых вторичными источниками на произвольной замкнутой поверхности 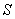, охватывающей точку 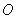в соответствии с выражением (5.1). Пусть 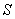сферическая поверхность радиуса 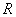c центром в точке 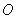. Тогда поле 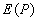в точке наблюдения 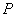можно представить суммой полей 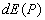, доставляемых электромагнитной волной от бесконечного множества шаровых сегментов 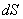(рис. 5.10):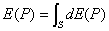

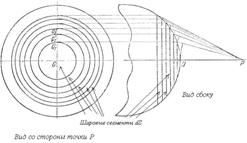
Рассмотрим 'механизм' формирования значения поля 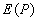последовательно, начиная от центрального шарового сегмента, центр которого пересекается прямой, соединяющей точки и (рис. 5.10). Приближённо на первом этапе рассуждений можно полагать, что амплитуды волн от соседних шаровых сегментов равны. Однако фазы этих волн отличаются из-за того, что волны проходят разный путь, тем больший, чем дальше рассматриваемый сегмент расположен от центрального (рис. 5.10). В первом приближении, можно полагать, что фаза меняется линейно в зависимости от пройденного волной расстояния от соответствующего шарового сегмента. По этой причине комплексная амплитуда 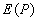, определяемая (5.5), представляет собой сумму бесконечно большого количества комплексных векторов одинаковой амплитуды, но повёрнутых по отношению к соседнему на одинаковый, бесконечно малый угол. На рис. 5.11a показано в виде комплексного вектора значение 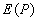, соответствующее такой части поверхности 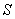, когда малые шаровые сегменты создают в точке наблюдения поле, фаза которого отличается на 180^о от фазы волны центрального сегмента. Рассмотренная часть поверхности 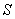волнового фронта получила название первой зоны Френеля. Границей, отделяющей первую зону Френеля от остальной части поверхности волнового фронта 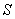, является окружность, в каждой точке которой фаза волн, приходящих в точку наблюдения 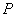, отличается на 180^о от фазы волны центрального сегмента.

Обратим внимание, что комплексная амплитуда поля, создаваемая первой зоной Френеля, определяется вектором, обозначаемым 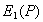и совпадающим с диаметром полуокружности, к которой стремится в пределе годограф кривой, представляющей сумму полей, создаваемых бесконечно малыми шаровыми сегментами. Фаза волны, создаваемой первой зоной Френеля, как следует из рис. 5.11a, отстаёт на 90^о от фазы волны 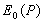, создаваемой центральным сегментом.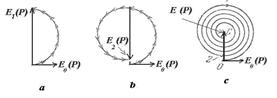

Если подвергнуть поверхность 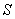дальнейшему разбиению на зоны, то получим вторую зону Френеля (рис. 5.12), граничащую с первой зоной и отделённую от остальной части поверхности 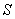окружностью, в каждой точке которой фаза волн, приходящих в точку наблюдения отличается на 180^о от фазы волн от границы с первой зоной Френеля. Можно заметить, что волны от второй зоны Френеля уменьшают комплексную амплитуду волн, создаваемых первой зоной Френеля, ввиду их противофазного сложения. В первом приближении, если не учитывать убывание амплитуды сферических волн обратно пропорционально расстоянию, сумма волн от первой и второй зон Френеля равна нулю. Но на самом деле, сумма волн, создаваемых первой и второй зоной Френеля хотя и имеет малую величину, но не равна нулю. Поэтому характер годографа волн, создаваемых первой и второй зоной Френеля, в пределе представляет часть некоторой спирали (рис. 5.11b).

Рис. 5.12.

Аналогичным образом продолжая разбиение поверхности на зоны, т.е. рассматривая третью, четвёртую и т.д. зоны Френеля (рис. 5.12), получим, что соседние чётные и нечётные зоны Френеля ослабляют поля, создаваемые каждой, и вместе образуют годограф, определяющий в пределе величину поля источника в точке наблюдения, в виде некоторой спирали (рис. 5. 11c).

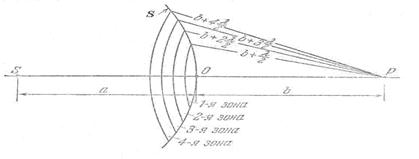
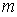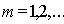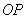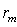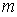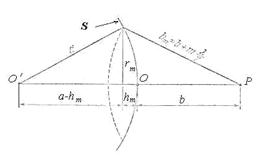
Границам зон Френеля на спирали соответствуют диаметрально противоположные точки её витков (рис. 5.11c), каждой из которых, соответствуют определяющие её границы радиус на поверхности . Так, граница - ой зоны Френеля () отстоит от прямой (рис. 5.12) на расстоянии , называемом радиусом - ой зоны Френеля. Найдём радиус 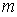- ой зоны Френеля. Как следует из геометрических соображений (рис. 5.13a):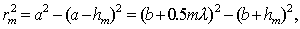

где 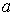- расстояние вдоль прямой 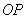от источника до центра волнового фронта; - расстояние вдоль прямой 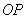от центра волнового фронта до точки наблюдения.

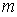Из (5.6a), пренебрегая , для не очень больших найдём :

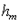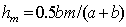
С помощью этого соотношения из (5.6а) найдём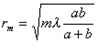

В частном случае бесконечно удалённого источника от точки наблюдения (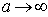) волновой фронт 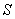является плоскостью и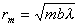

Характерной особенностью спирали (рис. 5.11c) является положение фокуса этой кривой, на который она 'наматывается' при бесконечно большом числе зон Френеля. Покажем, что фокус располагается в центре полуокружности первого витка спирали (рис. 5.11c), т.е. величина, поля создаваемого первой зоной Френеля, в два раза больше величины поля, создаваемой источником 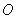в точке наблюдения .

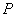Действительно, пусть 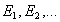- комплексные амплитуды, создаваемые первой, второй и т.д. зонами Френеля. Тогда искомая комплексная амплитуда в точке 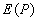, создаваемая всеми зонами Френеля в точке наблюдения, равна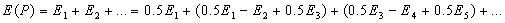

Как было отмечено выше, можно считать, что вклады от соседних зон примерно равны и их величины монотонно уменьшаются. По этой причине можно считать выражения в скобках в (5.7) равными нулю, т. е. имеет место равенство для любого :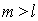

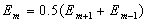
Тогда из выражения (5.7) получим: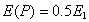

Учитывая, что интенсивность волны пропорциональна квадрату модуля электромагнитных векторов, можно заключить, что интенсивность поля 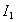, создаваемого первой зоной Френеля, в четыре раза больше интенсивности волны источника 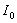в точке наблюдения, создаваемой всеми вторичными источниками на поверхности :

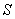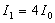
Четырёхкратное уменьшение интенсивности волны, создаваемой первой зоной Френеля, по отношению к интенсивности волны, создаваемой источником в точке наблюдения, связано с упомянутым выше противофазным вычитанием волн от различных зон Френеля на поверхности волнового фронта.

Приближённо, не принимая во внимание уменьшение интенсивности сферической волны с расстоянием, которое она проходит, в расчётах можно полагать, что величиной (5.9) определяется интенсивность волны, создаваемой каждой из зон Френеля, близкой к первой. Это является следствием равенства площадей зон Френеля, соответствующих различным значениям m. Действительно, принимая во внимание (рис. 5.13), находим площадь 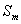сферического сегмента радиуса 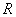и высоты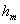

,

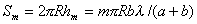(5.10a)

и получаем, что площадь 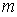- ой зоны Френеля :

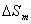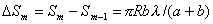
не зависит от .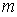

5. Дифракция Френеля от простейших преград.

Поставим на пути сферической световой волны непрозрачный экран с круглым отверстием радиуса 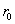. Экран расположен так, что перпендикуляр, опущенный из S на непрозрачный экран, попадает точно в центр отверстия

На продолжении этого перпендикуляра возьмем точку M и рассмотрим, что мы будем наблюдать на экране.

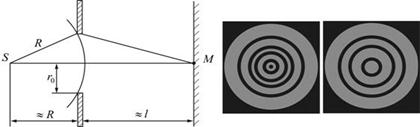
Разобьем открытую часть волновой поверхности на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, открываемых отверстием. Амплитуда результирующего колебания, возбуждаемого в точке М всеми зонами (9.2.1) и (9.2.2)

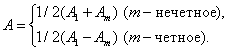
Таким образом, когда отверстие открывает нечетное число зон Френеля, то амплитуда (интенсивность) в точке М будет больше, чем при свободном распространении волны; если четное, то амплитуда (интенсивность) будет равна нулю, как показано на рис. 9.3.

Естественно, что если 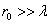, то никакой дифракционной картины не будет.

Дифракция от диска.

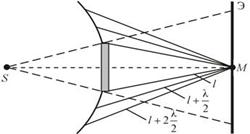
Точка M лежит на перпендикуляре к центру диска. Первая зона Френеля строится от края диска и т. д.

Амплитуда световых колебаний в точке M равна половине амплитуды, обусловленной первой открытой зоной. Если размер диска невелик (охватывает небольшое число зон), то действие первой зоны немногим отличается от действия центральной зоны волнового фронта. Таким образом, освещенность в точке M будет такой же, как и в отсутствие экрана. Вследствие симметрии центральная светлая точка будет окружена кольцами света и тени (вне границ геометрической тени).

Дата добавления: 2014-01-04