О.1 Метод Мора

Нехай для балки, що працює на прямий згин при довільному навантаженні системою сил Р (рис. 10.1, а), треба визначити прогин У_А= 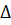_1F у довільному перерізі А. Для цього треба вибрати фіктивну балку (ф.б.) (задана балка без си­лових факторів) і у точці А прикласти фіктивну безрозмірну одиничну силу (рис. 10.1 б).

До цих двох зрівноважених станів навантаження застосуємо принцип мож­ливих переміщень, згідно з яким

A+V=0,

тобто у випадку рівноваги сил сума можливих робіт зовнішніх і внутрішніх сил, прикладених до системи, дорівнює нулеві. Беручи до уваги лише вплив згинальних моментів, одержимо

звідки

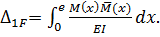(10.1)

Одержана формула називається інтегралом Мора для визначення перемі­щень від діїзгинальних моментів.

Інтеграл Мора для визначення переміщень з врахуванням поздовжніх сил, згинальних і крутних моментів запишеться у вигляді

(10.2)

Коли вирази для внутрішніх сил є різними для різних ділянок стержня, треба обчисляти інтеграли Мора для окремих ділянок і результати підсумовува­ти.

Для визначення кутових переміщень треба у перерізі, кут повороту якого шукається, прикласти фіктивний одиничний момент 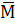= 1.

10.2 Обчислення інтегралів Мора за способом Верещагіна

Обчислення інтегралів Мора суттєво спрощується, якщо одна з епюр пря­молінійна. Така умова завжди виконується для систем, які складаються з пря­мих стержнів, так як епюри від одиничного навантаження обмежені прямими лініями.

Обчислимо інтеграл Мора , для випадку, коли грузова епюра M від заданого навантаження довільна, а від одиничного навантаження балки зображена прямою, рівняння якої можна записати так

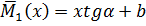(рис. 10.2)

Підставляючи цей вираз у формулу інтеграла Мора, одержимо

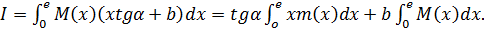(10.2)

Другий інтеграл в (10.2) являє собою площу грузової епюри згинальних моментів М і яку позначимо через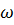

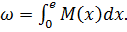(10.3)

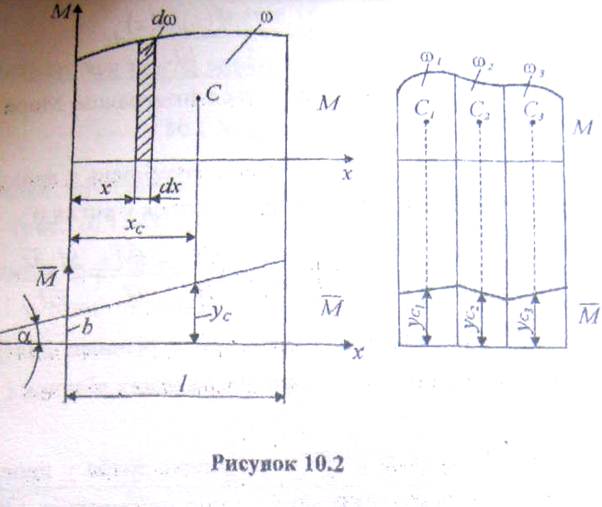
Перший інтеграл в (10.2) — це статичний момент цієї площі відносно осі М, який можна зобразити так:

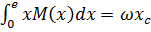(10.4) (10.4)

де х_с — абсциса центра ваги С епюри М

Підставляючи (10.3) і (10.4) в (10.2), одержимо

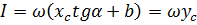(10.5) (10.5)

де у_с — ордината з одиничної епюри 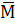, яка береться під центром ваги грузової епюри М.

Якщо епюра М — лінія ламана, обчислення інтегралу Мора за формулою (10.5) проводиться по ділянках, на кожній з яких епюра 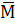— прямолінійна (рис. 10.3), Тоді

Підставляючи (10.5) в (10.1), одержимо остаточно формулу Верещагіна для визначення переміщень при дії згинальних моментів

(10.6)

10.3 Обчислення інтеграла Мора за формулою Сімпсона-Корноухова

Як відомо з інтегрального числення, якщо проміжок інтегрування l розби-1

ти на дві ділянки, то за формулою Сімпсона

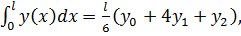(10.7)

Де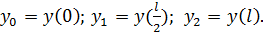

Позначимо M(х) 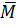(х)=у(х) і використовуючи для обчислення інтеграла Мора формулу Сімпсона (10. 7), одержуємо

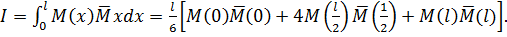(10.8)

Якщо позначити (рис. 10.3)

M(0)= a; M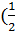)= f; M(l)=b; 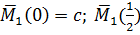=g;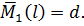

то (10.8) запишеться у вигляді

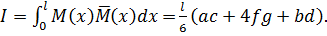(10.9)

На таку можливість спрощення обчислення інтеграла Мора вперше вказав український вчений Корноухов, тому і формула (10.9) називається формулою Сімпсона-Корноухова.

У загальному випадку функції y(x) формула Сімgсова (10.7) ‘ наближе­ною. Але якщо підінтегральна функція у(х) с поліномом не вище третього сте­пеня, то формула (10.7) дає точний результат. Отже, якщо М(х) — квадратна парабола, а 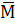(х) — лінійна функція, то формула (10.9) є точною.

Формулою (10.9) слід користуватись, коли важко знайти площу або центр ваги грузової епюри М.

Лекція 11

СТАТИЧНО НЕВИЗНАЧЕНІ СИСТЕМИ

11.1 Ступінь статично невизначеної системи

Як вже раніше вказувалось, статично невизначеними називаються системи, в яких реакції і внутрішні силові фактори не можна знайти тільки з рівнянь ста­тики. В таких системах більше зв'язків, ніж тих, що потрібні для рівноваги. Та­кі зв'язки називаються зайвими, а зусилля в них — зайвими невідомими. Кіль­кість зайвих невідомих вказує ступінь статичної невизначеності системи.

На рис. 11.1а показана балка на двох опорах — система статично визначе­на і геометрично незмінна. Всі три реакції (R_А, Н_А, R_B) визначаються з трьох рівнянь статики. Використовуючи метод перерізів, можна знайти Q(x) і М(х) в довільному перерізі.

Додамо ще один зв'язок, наприклад, шарнірно-рухому опору в перерізі С (рис. 11.1 б). Хоча в результаті цього система стала більш міцною і жорсткою, однак з точки зору геометричної незмінності цей зв'язок зайвий. Тепер з 3 рів­нянь рівноваги чотири реакції (R_А, Н_А, R_В,R_С) знайти не можна. Таким чином, балка на рис. 11.1 б, один раз статично невизначена.

На рис. 11.2 а балка один раз статично невизначена. На рис. 11.2 б, в балки два рази статично не визначені.

N11.2 Канонічні рівняння методу сил

Розрахунок статично невизначеної балки пояснимо на прикладі балки, по­казаної на рис. 11.3 а.

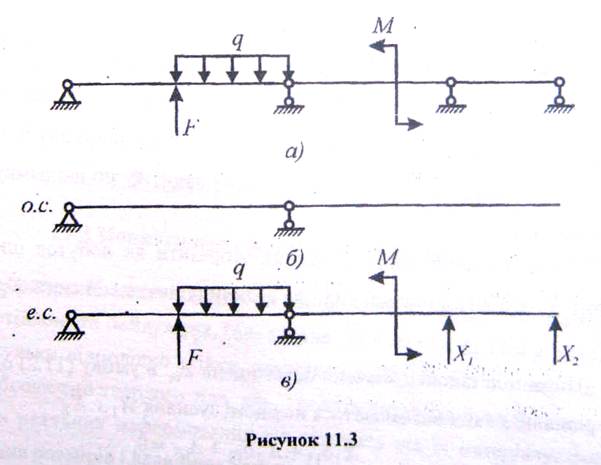
1. Встановлюємо ступінь статичної невизначеності балки. Кількість неві­домих реакцій - 5; кількість рівнянь статики - 3; різниця 5-3=2, отже, балка двічі статично невизначена.

2. Відкидаючи зайві зв'язки, утворюємо основну систему (рис. 11.3 б). Ос­новна система (о.с.) повинна бути статично визначеною і геометрично незмін­ною. Можливі різні варіанти основних систем. Раціональний вибір о.с. спрощує розрахунок.

3. Навантажуємо основну систему заданим навантаженням і реакціями від­кинутих зв'язків. Така система називається еквівалентною системою (е.с.) рис. 11.3 в.

4. Щоб деформації і внутрішні зусилля заданої системи і еквівалентної бу­ли однаковими, прирівнюємо до нуля переміщення точок прикладання невідо­мих реакцій по напрямку їх дії. Тобто

(11.1)

На основі закону незалежності дії сил можна кожне і переміщень зо­бразити як суму переміщень від дії зайвих невідомих і переміщень від дії зада­ного навантаження. Тоді (11.1) набувають вигляду

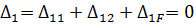
(11.2)

- Перший індекс при 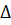означає точку і напрямок її переміщення, другий вказує від якого складового фактору шукається переміщення. Наприклад, — це переміщення точки прикладанні сили Х₁ по напрямку ЇЇ дії від сили Х₂; 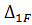— це переміщення точки прикладання сили X₁ по напрямку її дії від зада­ного навантаження.

Кожне з переміщень можна зобразити як добуток питомого перемі­щення від дії одиничної сиди на величину невідомої сили Х_K

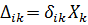
Після підстановки значень переміщень 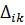в умову (11.2) одержимо систе­му рівнянь, з яких визначаються невідомі зусилля Х₁ і Х₂

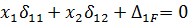
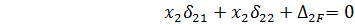(11.3)

Рівняння (113) називаються канонічними рівняннями методу сил. Така на­зва вказує на те, що ці рівняння записуються за відповідним правилом (кано­ном) і невідомими в цих рівняннях с сили або моменти, які являють собою реа­кції відкинутих зв'язків. Кількість таких рівнянь дорівнює ступеню статичної невизначеності заданої системи.

Питомі переміщення, які мають однакові індекси, називаються головними коефіцієнтами, а питомі переміщення, які мають неоднакові індекси — бічними коефіцієнтами канонічних рівнянь.

Переміщення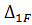і, які входять в канонічні рівняння (11.3), як правило визначають за методом Мора або за способом Верещагіна. Якщо для балки або рами прямокутного перерізу відношення висоти перерізу до довжини прольоту <0,2, то при визначенні переміщень впливом поперечних сил можна знех­тувати.

Слід мати на увазі, що в реальних балочних або рамних конструкціях від­ношення h/l < 0,1. Тому при визначенні переміщень за формулою Мора доцільно враховувати лише згинальні моменти. Тоді за формулою (10.1)

;

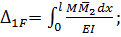
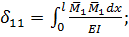
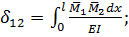
На основі теореми про взаємність переміщень коефіцієнти мають влас­тивість

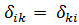
СТІЙКІСТЬ СТИСНУТИХ СТЕРЖНІВ

11.3 Поняття про стійкі і нестійкі форми рівноваги

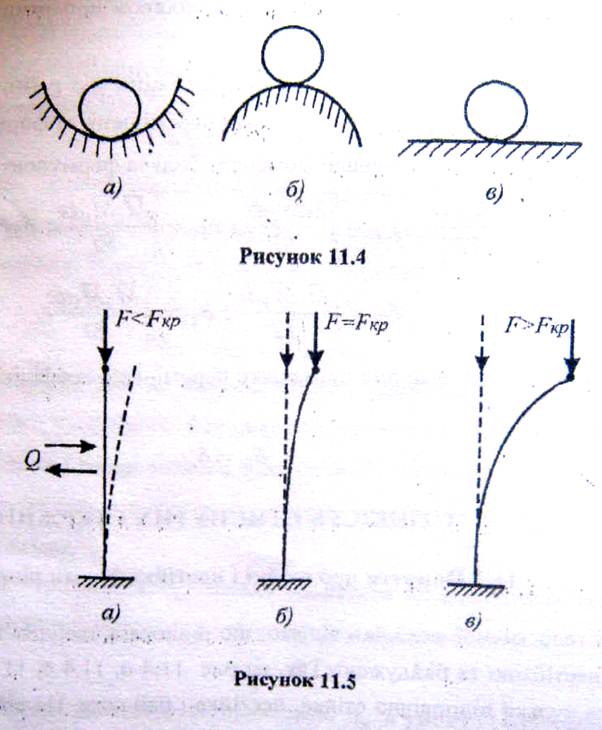
З теоретичної механіки відомо, що рівновага твердих тіл може бути стій­кою, нестійкою та байдужою. Так, на рис. 11.4 а, 11.4 б, 11.4 в положення рів­новаги кульки відповідно стійке, нестійке і байдуже. На відміну від форм рів­новаги абсолютно твердого тіла, які залежать лише від його положення, форми рівноваги реальних деформованих тіл залежать від їх матеріалу, форми, спів­відношення розмірів і величини прикладених сил.

Розглянемо рівновагу прямого стержня, який стискається силою F. До пе­вної величини стискаючої сили F стержень, відхилений від вертикального по­ложення силою Q, під дією внутрішніх сил повертається у початковий стан, якщо силу Q усунути; це означає, що його прямолінійна форма рівноваги є стійкою (рис. 11.5 а). Коли сила F досягає критичного значення, яке ми позна­чимо через F _кр, стержень, виведений із прямолінійної форми, може повернути­ся до неї, але може також залишитися злегка зігнутим, коли сила Q перестала діяти (рис. 11.5 б). Якщо F > F _кр, прямолінійна форма рівноваги не зберігаєть­ся, стержень сильно скривлюється і набуває нової, криволінійної форми рівно­ваги (рис. 11.5 в) або руйнується.

Отже, критичною силою для прямого стержня ми називаємо ту найменшу стискуючу силу F_min, прямолінійна форма рівноваги стержня стає не­стійкою.

При розрахунку на стійкість критична сила аналогічна руйнуючій при роз­рахунку на міцність. Щоб забезпечити стійкість, необхідно, щоб F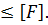

Тут

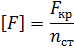
де - допустимий коефіцієнт запасу стійкості.

Лекція 12

12.1 Визначення критичної сили за формулою Ейлера

Для розрахунків стиснених стержнів на стійкість треба знати способи ви­значення критичної сили F^. Розглянемо стиск стержня силою F, величина якої трохи більше, ніж F _кр і стержень знаходиться у злегка зігнутому стані (рис. 12.1 а).

Диференціальне рівняння зігнутої осі стержня маг вигляд

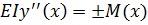(12.1)

Так як абсолютна величина згинального моменту

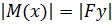
а знак прогину у і другої похідної у" завжди протилежні, то рівняння (12.1) мас вигляд

(12.2)

Зауважимо, що незалежно від того, куди зігнеться стержень: вліво (рис. 12.1 а) або вправо (рис. 12.1 б) і незалежно від вибору осі у, диференціальне рівняння завжди має вигляд (12.2).

Запишемо (12.2) у вигляді

=0

або

(12.3)

де

(12.4)

Загальний розв'язок цього однорідного лінійного диференціального рів­няння записується, як відомо, так:

(12.5)

Сталі інтегрування А і В визначаємо з граничних умов

y(0)=0; y(l)=0

З першої умови маємо

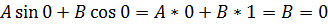
З другої умови одержуємо

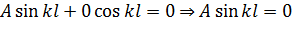(12.6)

Оскільки А≠ 0 (в протилежному разі не було б згину стержня, бо якщо A = 0 і B = 0, то у 0, а ми припустили, що стержень зігнувся), то

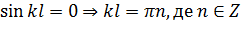(12.7)

Визначаємо з (12.7) к і підставимо в (12.4), знаходимо

F= (12.8)

Найменше значення F=F _кр відмінне від нуля, одержимо з (12.8) при

I=I _min і n=1. Тоді

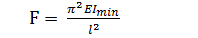(12.9)

Формула (12.9) вперше була одержана Ейлером у 1744 р. і називається формулою Ейлера для критичної сили для стержня з шарнірним закріпленням кінців. Значенню F = F _кр відповідає зігнута вісь стержня у вигляді півхвилі синусоїди (рис. 12.1 а) з рівнянням

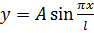(12.10)

Найбільший прогин стержня у_тах = А при х=l/2. Отже, А — це найбіль­ший прогин посередині стержня.

З формули (12.9) видно, що F_кр пропорційна найменшій жорсткості стер­жня ЕІ_тіп, гак як очевидно, що прогин стержня відбувається завжди в площині найменшої жорсткості, яка перпендикулярна до осі z, відносно якої момент інерції поперечного перерізу стержня I_z = I_min..

Для визначення критичної сили при інших способах закріплення кінців стержня треба знов інтегрувати рівняння (12.3) при відповідних граничних умовах. Наведемо формулу Ейлера без доведення для загального випадку

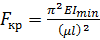(12.11)

де µl — зведена довжина стержня, а µ — коефіцієнт зведення довжини, який залежить від способу кріплення кінців стержня. На рис. 12.2 зображено способи кріплення кінців стержня, які найчастіше застосовують, і наведено значення µ.

12.2 Межі придатності формули Ейлера. Формула Ясинського

Виведення формули Ейлера грунтується на законі Гука, який дійсний доти, поки напруження не перевищує межі пропорційності σ _пц. Для визначення меж застосування формули Ейлера знайдемо критичне напруження в стержні σ _кр,яке виникає під дією критичної сили. Розділивши F_кр на площу поперечного перерізу стержня А, одержимо

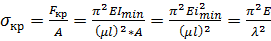(12.12)

де і_тіп = 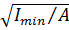— мінімальний радіус інерції поперечного перерізу стержня; λ— гнучкість стержня, безрозмірна величина. Формулою Ейлера мо­жна користуватися тільки тоді, коли

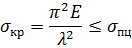
Отже,

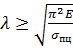(12.13)

Величину, яка стоїть у правій частині (12.13), називають граничною гнучкістю і позначають 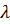_гр. Так, для Ст3 маємо σ _пц = 200МПа, а E=2*10⁵МПа,

тоді

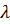_гр=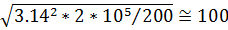

Якщо гнучкість стержня менша від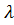 _гр, то формулами Ейлера (12.11) і (12.12) користуватись не можна. Так, для сталі Ст3 при гнучкостях 405≤ 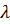<100 критичне напруження визначається за емпіричною формулою Ясинського

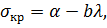(12.14)

де α= 310 МПа, b = 1,14 МПа — коефіцієнти, які визначаються з дослідів.

При гнучкостях 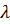<40 за критичне напруження приймається σ _Т =240МПа.

Отже, для стержнів з матеріалу Ст3 з малою гнучкістю (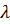<40) σ _кр = σ _Т; з середньою гнучкістю (40 ≤ 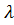< 100) 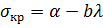; з великою гнучкістю (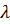≥100) . Графік залежності σ_кр від 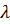для стержнів з маловуглецевої ста­лі Ст3 зображено на рис. 12.3.

Лекція 13

КОЛИВАННЯ СИСТЕМ З ОДНИМ СТУПЕНЕМ ВІЛЬНОСТІ

13.1 Основні поняття теорії коливань

Пружні системи, що зазнають коливань, поділяються за числом ступенів вільності. Числом ступенів вільності називається кількість незалежних коорди­нат, що визначають положення мас системи.

Наприклад, проста балка з прикріпленим до неї вантажем з масою т (рис. 13.1 а), вісь якої коливається у вертикальній площині, буде системою з одним ступенем вільності, коли масою балки можна нехтувати порівняно з масою ван­тажу. Положення вантажу при коливаннях визначається лише однією координатою — переміщенням у його центр ваги відносно положення рівноваги. Ана­логічно, балка з двома прикріпленими до неї вантажами з масами m₁, і m₂ (рис. 13.1 б), буде системою з двома ступенями вільності.

Залежно від характеру сил, що підтримують коливання, розрізняють вільні і вимушені коливання. Вільними називаються коливання, що відбуваються під дією одних лише сил пружності системи. У реальних умовах вільні коливання внаслідок дії сил опору поступово затухають і система приходить у стан спо­кою. Вимушені коливання відбуваються при активній дії зовнішніх сил, зде­більшого періодичних, які підтримують коливальний рух. Залежно від напрямку коливань відносно осі стержня розрізняють його поздовжні, поперечні і крутильні коливання.

13.2 Вільні коливання балки з одним ступенем вільності

Розглянемо вільні коливання системи з одним ступенем вільності, наприк­лад, невагомої балки з прикріпленим до неї вантажем вагою Р (рис.13.2 а). Під дією ваги Р балка зігнеться і вантаж зміститься вниз на величину

(13.1)

де с — жорсткість балки.

Приймемо координатну вісь ОY з початком у центрі ваги вантажу після його статичного переміщення. Якщо вантаж змістити вниз на величину у і по­тім відпустити, то він почне коливатися під дією пружної реакції балки віднос­но рівноважного положення О, яке він займав при статичній деформації балки.

Нехай у довільний момент часу t вантаж рухається вниз. На нього діє сила Р напрямлена вниз і сила пружної реакції балки F_пр напрямлена вгору (рис.13.2 б). За другим законом Ньютона

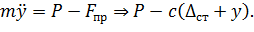(13.2)

де .

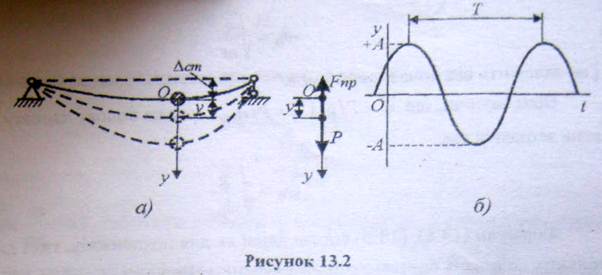
Підставляючи (13.1) в (13.2), одержимо

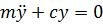(13.3)

Одержане рівняння — це диференціальне рівняння вільних коливань системи з одним ступенем вільності. Вводячи позначення

(13.4)

запишемо рівняння (13.3) у вигляді

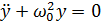(13.5)

Загальний розв'язок цього рівняння

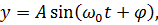(13.6)

де А, 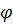— довільні сталі інтегрування.

Це рівняння називається рівнянням вільних коливань системи. Графік цих коливань показаний на рис. 13.2, б.

Стала А, тобто величина найбільшого відхилення вантажу від рівноважного положення, називається амплітудою коливань, стала 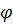— їх початковою фазою. З рівняння (13.6) видно, що переміщення у повторюється через проміжок часу Т що називається періодом коливань i

(13.7)

Величин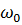а = 2 /Т, що є числом коливань системи за 2 секунд, назива­ється коловою частотою коливань.

На основі залежності (13.4) видно, що

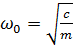(13.8)

і не залежить від початкових умов.

Враховуючи, що m=P/g і с = Р/ 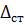, можна колову частоту вільних коли­вань записати так

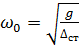(13.9)

Формули (13.8), (13.9) справедливі як для поздовжніх, так і для крутильних вільних коливань систем з одним ступенем вільності.

13.3 Вимушені коливання систем з одним ступенем вільності

Сила, що викликає вимушені коливання, називається збурюючою силою. Нехай збурююча сила прикладена до системи в тому ж перерізі, де прикріпле­ний вантаж Р, і величина ЇЇ змінюється за законом

,

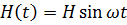де H — найбільше значення збурюючої сили,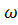— її колова частота.

Диференціальне рівняння вимушених коливань системи з одним ступенем вільності має вигляд

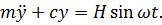(13.10) (13.10)

Частковий розв'язок цього рівняння шукаємо у вигляді

. (13.11) (13.11)

Підставимо (13.1) в (13.10). Одержимо рівність

,

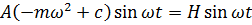яка перетворюється на тотожність, коли

З останнього рівняння знаходимо

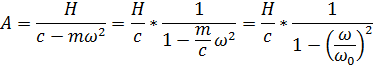
Одержану формулу для амплітуди вимушених коливань можна записати

(13.12)

де β називається коефіцієнтом зростання коливань і

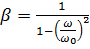. (13.13)

Коли , тобто при резонансі, коефіцієнт β, а разом з ним і амплітуда вимушених коливань необмежено зростають. У реальних умовах амплітуда ви­мушених коливань при резонансі не зростає необмежено внаслідок наявності сил опору.

Максимальне динамічне переміщення можна зобразити як суму стати­чного переміщення 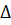_ст від дії сили Р і амплітуди вимушених коливань

,

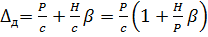або

де к_д — динамічний коефіцієнт, що дорівнює

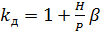(13.14)

Оскільки в межах справедливості закону Гука напруження пропорційні деформаціям, то при вимушених коливаннях динамічне напруження σ _д дорів­нює

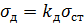(13.15)

а умова міцності має вигляд

(13.16)

Лекція 14

УДАРНІ НАВАНТАЖЕННЯ. ДИНАМІЧНИЙ КОЕФІЦІЄНТ ПРИ УДАРІ

14.1 Основні поняття і припущення

Ударним навантаженням називають навантаження, яке передається на тіло протягом малого проміжку часу і викликає значні прискорення в тілі, що зазнає удару.

Розрахунок на дію ударного навантаження проводиться у так званій технічній теорії удару, в основу якої покладені такі припущення:

1.Під час удару виникають тільки пружні деформації, тобто після припинення дії ударного навантаження тіло повертає свої початкові форму і розміри.

2.Для ударного навантаження матеріалу розраховуваного елемента конструкції дійсний закон Гука.

3. Удар вважають абсолютно непружним, тобто ударний вантаж після удару не відскакує від пружної системи, а продовжує в процесі дії деформації ру­хатися разом з нею.

4.Маса пружної системи, яка приймає удар, мала порівняно з масою ударного тіла, і тому масою пружної системи можна нехтувати.

5.Робота падаючого (ударного) тіла повністю переходить у потенціальну енергію деформації елемента конструкції, який сприймає дію удару.

На основі цих припущень визначимо напруження і деформації, що виникають у стержневих елементах при ударі.

14.2 Поздовжній удар

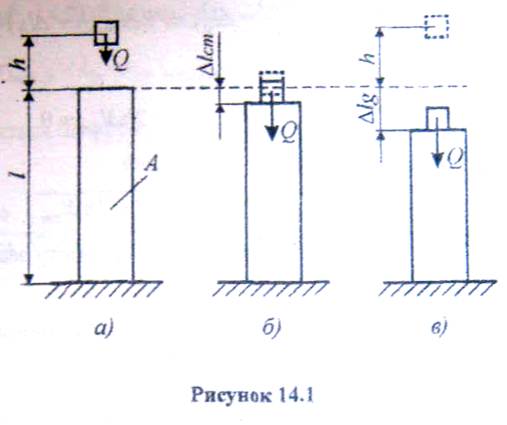
Розглянемо систему, яка складається з вертикального пружного стержня і вантажу Q, який падає на цей стержень (рис. 14.1, а).

Розглянемо два випадки:

1) вантаж Q прикладається до стержня статично і стискає стержень на величину 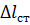(рис. 14.1, б);

2) вантаж падає на стержень з висоти к і стискає стержень на величину 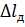(рис. 14.1, в).

Зміна деформації стержня при ударному навантаженні Q порівняло з де­формацією при статичній дії сили Q характеризується коефіцієнтом динаміч­ності

(14.1)

З фізичних міркувань очевидно, що к_д > 1.

Враховуючи лінійний зв'язок між напруженнями і деформаціями по анало­гії з формулою (14.1) одержимо

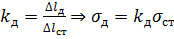(14.2)

де

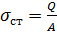(14.3)

— напруження, що виникає в стержня при статичній дії сили Q.

За законом Гука

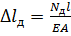; (14.4)

На основі закону збереження енергії робота, яку виконує вантаж під час падінні дорівнює потенціальній енергії деформації стержня:

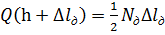(14.5)

де N_д — найбільша величина динамічної сили при ударі.

З (14.4) визначаємо і підставляємо в (14.5)

;

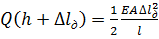
або

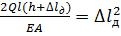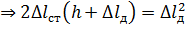; (14.6)

Одержаний вираз перепишемо так

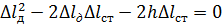(14.7)

Звідси знаходимо динамічну деформацію

(14.8)

Так як знак мінус не відповідає фізичному змісту задачі, то в (14.8) беремо знак плюс.

Враховуючи (14.1), знаходимо коефіцієнт динамічності

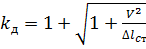(14.9)

Оскільки h = 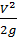(V — швидкість вантажу в момент удару), то коефіцієнт динамічності можна визначати ще так:

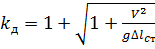(14.10)

Звернемо увагу, що при h = 0, тобто, коли сила прикладається миттєво, то з (14.9) або з (14.10) одержимо k_д = 2. Отже, при динамічному навантаженні стержня переміщення, зусилля і напруження у два рази більше від відповідних статичних величин.

Використовуючи формулу (14.2), визначимо динамічні напруження при ударі

. (14.11)

Дата добавления: 2014-01-04