Интервальная оценка результатов измерения при Гауссовом законе распределения

Интервальная оценка - это такая оценка, которой можно оценить истинное значение:

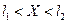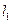, гдеи 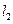– это границы интервала.

В результате измерений 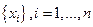, мы можем строить только вероятностные характеристики. То есть найти оценку границ: .

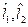Ставится вопрос: какова вероятность того, что истинное значение попадет в интервал ?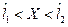

Вероятность такого события называется доверительной вероятностью, а оценка – доверительным интервалом.

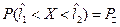
В результате измерений выборки 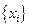мы знаем 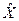, поэтому границы доверительного интервала строятся на основе экспериментально полученной оценки истинного значения.

При определенной доверительной вероятности, доверительный интервал будет узким, а при какой-то иной – широким. Поэтому в качестве оценки нижней границы принимается величина 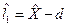, а в качестве верхней - 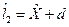, где 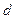- полуширина доверительного интервала.

Рассмотрим 2 случая:

1) 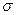- известно

Оценка: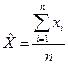

Плотность вероятности: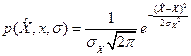

Найдем вероятность: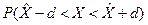

a) Величина 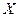- детерминированная не интегрируем

b) Приведем к виду, чтобы можно было проинтегрировать:

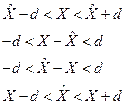
Тогда ,

произведя замену 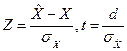, получим .

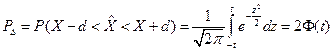Где 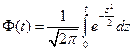- функция Лапласа. Она нечетная, табулированная.

Таким образом, доверительная вероятность есть удвоенное значение функции Лапласа.

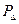
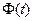
Находим 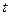и вычисляем искомую величину : .

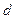Запись результата: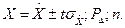

Запишем .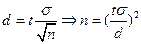

Общая постановка:

Требуется при определенной доверительной вероятности и 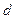оценить нужный объем выборки, чтобы обеспечить доверительную вероятность.

2) 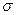- неизвестно

В качестве оценки результата измерения берется среднее значение

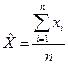, тогда 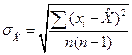- несмещенная оценка СКО.

То есть, если каждый результат измерений распределен по нормальному закону распределения, то 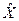- тоже по нормальному.

Поступаю следующим образом: вводят величину 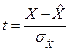, она распределена по закону Стьюдента. Плотность вероятности такого закона:

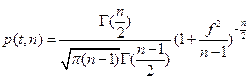, где 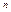- число наблюдений.

Если 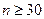, то закон Стьюдента аппроксимируют на практике нормальным законом.

,

Где 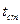- вероятностный коэффициент Стьюдента.

Далее находим по таблице 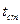, и получаем искомую величину - .

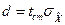Результат измерения записывается аналогично первому случаю: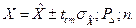

Дата добавления: 2014-01-04