Красно-черные деревья

Деки

Дек является особым видом очереди.

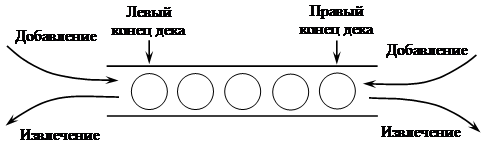
Дек (англ. deque – аббревиатура от double-ended queue, двухсторонняя очередь) – это структура данных, представляющая собой последовательность элементов, в которой можно добавлять и удалять в произвольном порядке элементы с двух сторон (рис. 3). Первый и последний элементы дека соответствуют входу и выходу дека.

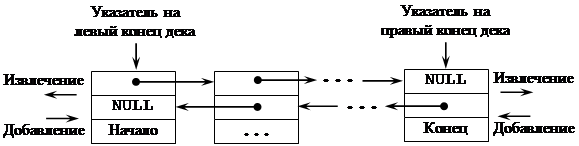Рис. 3. Дек и его организация

Частные случаи дека – это ограниченные деки:

· дек с ограниченным входом – из конца дека можно только извлекать элементы;

· дек с ограниченным выходом – в конец дека можно только добавлять элементы.

Данная структура является наиболее универсальной из рассмотренных выше линейных структур. Накладывая дополнительные ограничения на операции с началом и/или концом дека, можно осуществлять моделирование стека и очереди.

Однако применительно к деку целесообразно говорить не о начале и конце как в очереди, а о левом и правом конце.

Описание элементов дека аналогично описанию элементов линейного двунаправленного списка. Поэтому объявим дек через объявление линейного двунаправленного списка:

struct Deque {

Double_List *Begin;//начало дека

Double_List *End; //конец дека

};

..........

Deque *My_Deque;

Основные операции, производимые с деком:

· создание дека;

· печать (просмотр) дека;

· добавление элемента в левый конец дека;

· добавление элемента в правый конец дека;

· извлечение элемента из левого конца дека;

· извлечение элемента из правого конца дека;

· проверка пустоты дека;

· очистка дека.

Реализацию этих операций приведем в виде соответствующих функций, которые, в свою очередь, используют функции операций с линейным двунаправленным списком.

//создание дека

void Make_Deque(int n, Deque* End_Deque){

Make_Double_List(n,&(End_Deque->Begin),NULL);

Double_List *ptr; //вспомогательный указатель

ptr = End_Deque->Begin;

while (ptr->Next!= NULL){

ptr = ptr->Next;

}

End_Deque->End = ptr;

}

//печать дека

void Print_Deque(Deque* Begin_Deque){

Print_Double_List(Begin_Deque->Begin);

}

//добавление элемента в правый конец дека

void Add_Right_Item_Deque(int NewElem, Deque* End_Deque){

End_Deque->End =Insert_Item_Double_List(End_Deque->End,2,NewElem);

End_Deque->End = End_Deque->End->Next;

}

//добавление элемента в левый конец дека

void Add_Left_Item_Deque(int NewElem, Deque* Begin_Deque){

Begin_Deque->Begin =

Insert_Item_Double_List(Begin_Deque->Begin, 1, NewElem);

}

//извлечение элемента из левого конца дека

int Extract_Left_Item_Deque(Deque* Begin_Deque){

int NewElem = NULL;

if (Begin_Deque->Begin!= NULL) {

NewElem = Begin_Deque->Begin->Data;

Begin_Deque->Begin=Delete_Item_Double_List(Begin_Deque->Begin,0);

//удаляем вершину

}

return NewElem;

}

//извлечение элемента из правого конца дека

int Extract_Right_Item_Deque(Deque* End_Deque){

int NewElem = NULL;

if (End_Deque->End!= NULL) {

NewElem = End_Deque->End->Data;

Delete_Item_Double_List(End_Deque->End, 1);

//удаляем вершину

}

return NewElem;

}

//проверка пустоты очереди

bool Empty_Deque(Deque* Begin_Deque){

return Empty_Double_List(Begin_Deque->Begin);

}

//очистка очереди

void Clear_Deque(Deque* Begin_Deque){

Delete_Double_List(Begin_Deque->Begin);

}

Бинарные деревья работают лучше всего, когда они сбалансированы, когда длина пути от корня до любого из листьев находится в определенных пределах, связанных с числом вершин. Красно-черные деревья являются одним из способов балансировки деревьев. Название происходит от стандартной раскраски узлов таких деревьев в красный и черный цвета. Цвета вершин используются при балансировке дерева.

Красно-черное дерево (Red-Black-Tree, RB-Tree) – это бинарное дерево со следующими свойствами (рис. 4):

· каждая вершина должна быть окрашена либо в черный, либо в красный цвет;

· корень дерева должен быть черным;

· листья дерева должны быть черными и объявляться как NIL-вершины (NIL-узлы, то есть «виртуальные» узлы, наследники узлов, которые обычно называют листьями; на них «указывают» NULL указатели);

· каждый красный узел должен иметь черного предка;

· на всех ветвях дерева, ведущих от его корня к листьям, число черных вершин одинаково.

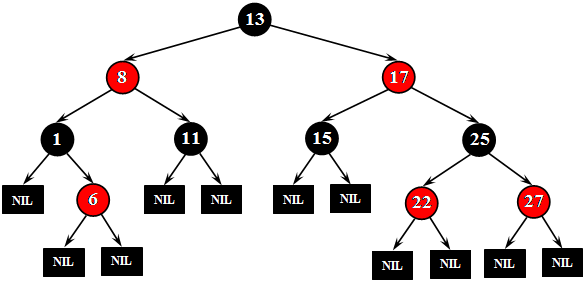
Рис.4. Красно-черное дерево

Количество черных вершин на ветви от корня до листа называется черной высотой дерева. Перечисленные свойства гарантируют, что самая длинная ветвь от корня к листу не более чем вдвое длиннее любой другой ветви от корня к листу.

Над красно-черными деревьями можно выполнять все те же основные операции, что и над бинарными деревьями.

Приведем функции следующих операций над красно-черными деревьями: создание дерева, печать (просмотр) дерева, обход дерева, проверка пустоты дерева и удаление дерева.

//создание красно-черного дерева

void Make_RBTree(RBTree** Node, int n){

int Data;

while (n > 0) {

cout << "Введите значение ";

cin >> Data;

Insert_Node(Node, Data);

n--;

}

}

//добавление узла в красно-черное дерево

void Insert_Node(RBTree** Node,int Data) {

RBTree **Curent, *Parent, *New_Node;

Curent = Node;

Parent = NIL;

// Поиск местоположения

while (*Curent!= NIL) {

Parent = (*Curent);

Curent = Data < (*Curent)->Data? &((*Curent)->Left): &((*Curent)->Right);

}

// Создание нового узла

New_Node = new RBTree();

New_Node->Data = Data;

New_Node->Parent = Parent;

New_Node->Left = NIL;

New_Node->Right = NIL;

New_Node->color = RED;

// Вставка элемента в дерево

if(Parent!= NIL){

if (Data < Parent->Data) Parent->Left = New_Node;

else Parent->Right = New_Node;

}

else (*Curent) = New_Node;

Insert_Fixup(Node, New_Node);

}

// Поддержка баланса дерева после вставки нового элемента

void Insert_Fixup(RBTree** Node,RBTree* New_Node){

RBTree* Current = New_Node;

// Проверка свойств дерева

while (Current!= *(Node) && Current->Parent->color == RED){

// если есть нарушение

if (Current->Parent == Current->Parent->Parent->Left) {

RBTree *ptr = Current->Parent->Parent->Right;

if (ptr->color == RED) {

Current->Parent->color = BLACK;

ptr->color = BLACK;

Current->Parent->Parent->color = RED;

Current = Current->Parent->Parent;

}

else {

if (Current == Current->Parent->Right) {

// сделать Current левым потомком

Current = Current->Parent;

Rotate_Left(Node,Current);

}

// перекрасить и повернуть

Current->Parent->color = BLACK;

Current->Parent->Parent->color = RED;

Rotate_Right(Node,Current->Parent->Parent);

}

}

else {

RBTree *ptr = Current->Parent->Parent->Left;

if (ptr->color == RED) {

Current->Parent->color = BLACK;

ptr->color = BLACK;

Current->Parent->Parent->color = RED;

Current = Current->Parent->Parent;

}

else {

if (Current == Current->Parent->Left) {

Current = Current->Parent;

Rotate_Right(Node,Current);

}

Current->Parent->color = BLACK;

Current->Parent->Parent->color = RED;

Rotate_Left(Node,Current->Parent->Parent);

}

}

}

(*Node)->color = BLACK;

}

//поворот узла Current влево

void Rotate_Left(RBTree** Node,RBTree *Current) {

RBTree *ptr = Current->Right;

Current->Right = ptr->Left;

if (ptr->Left!= NIL) ptr->Left->Parent = Current;

if (ptr!= NIL) ptr->Parent = Current->Parent;

if (Current->Parent!= NIL) {

if (Current == Current->Parent->Left)

Current->Parent->Left = ptr;

else

Current->Parent->Right = ptr;

}

else {

(*Node) = ptr;

}

ptr->Left = Current;

if (Current!= NIL) Current->Parent = ptr;

}

//поворот узла Current вправо

void Rotate_Right(RBTree** Node,RBTree *Current) {

RBTree *ptr = Current->Left;

Current->Left = ptr->Right;

if (ptr->Right!= NIL) ptr->Right->Parent = Current;

if (ptr!= NIL) ptr->Parent = Current->Parent;

if (Current->Parent!= NIL) {

if (Current == Current->Parent->Right)

Current->Parent->Right = ptr;

else

Current->Parent->Left = ptr;

}

else {

(*Node) = ptr;

}

ptr->Right = Current;

if (Current!= NIL) Current->Parent = ptr;

}

//печать красно-черного дерева

void Print_RBTree(RBTree* Node, int l){

int i;

if (Node!= NIL) {

Print_RBTree(Node->Right, l+1);

for (i=0; i< l; i++) cout << " ";

if (Node->color == RED)

SetConsoleTextAttribute(hStd,FOREGROUND_RED);

cprintf ("%4ld", Node->Data);

SetConsoleTextAttribute(hStd,atr);

Print_RBTree(Node->Left, l+1);

}

else cout << endl;

}

//прямой обход красно-черного дерева

void PreOrder_RBTree(RBTree* Node){

if (Node!= NIL) {

printf ("%3ld",Node->Data);

PreOrder_RBTree(Node->Left);

PreOrder_RBTree(Node->Right);

}

}

//обратный обход красно-черного дерева

void PostOrder_RBTree(RBTree* Node){

if (Node!= NIL) {

PostOrder_RBTree(Node->Left);

PostOrder_RBTree(Node->Right);

printf ("%3ld",Node->Data);

}

}

//симметричный обход красно-черного дерева

void SymmetricOrder_RBTree(RBTree* Node){

if (Node!= NIL) {

PostOrder_RBTree(Node->Left);

printf ("%3ld",Node->Data);

PostOrder_RBTree(Node->Right);

}

}

//проверка пустоты красно-черного дерева

bool Empty_RBTree(RBTree* Node){

return (Node == NIL? true: false);

}

//освобождение памяти, выделенной под красно-черное дерево

void Delete_RBTree(RBTree* Node){

if (Node!= NIL) {

Delete_RBTree(Node->Left);

Delete_RBTree(Node->Right);

delete(Node);

}

}

Дата добавления: 2014-01-04