Методы оценки ресурсной эффективности алгоритмов

Основными алгоритмическими конструкциями в процедурном программировании являются следование, ветвление и цикл. Для получения функций трудоемкости для лучшего, среднего и худшего случаев при фиксированной размерности входа необходимо учесть различия в оценке основных алгоритмических конструкций.

· Трудоемкость конструкции «Следование» есть сума трудоемкостей блоков, следующих друг за другом:

.

· Трудоемкость конструкции «Ветвление» определяется через вероятность перехода к каждой из инструкций, определяемой условием. При этом проверка условия также имеет определенную трудоемкость. Для вычисления трудоемкости худшего случая может быть выбран тот блок ветвления, который имеет большую трудоемкость, для лучшего случая – блок с меньшей трудоемкостью.

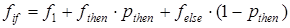
· Трудоемкость конструкции «Цикл» зависит от вида цикла. Для цикла с параметрами будет справедливой формула:

, где n – количество повторений тела цикла, f – трудоемкость тела цикла.

Реализация цикла с предусловием и с постусловием не меняет методики оценки его трудоемкости. На каждом проходе выполняется оценка трудоемкости условия, изменения параметров (при наличии) и тела цикла. Общие рекомендации для оценки циклов с условиями затруднительны. Так как в значительной степени зависят от исходных данных.

· В случае использования вложенных циклов их трудоемкости перемножаются.

Таким образом, для оценки трудоемкости алгоритма может быть сформулирован общий метод получения функции трудоемкости.

1. Декомпозиция алгоритма предполагает выделение в алгоритме базовых конструкций и оценку и трудоемкости. При этом рассматривается следование основных алгоритмических конструкций.

2. Построчный анализ трудоемкости по базовым операциям языка подразумевает либо совокупный анализ (учет всех операций), либо пооперационный анализ (учет трудоемкости каждой операции).

3. Обратная композиция функции трудоемкости на основе методики анализа базовых алгоритмических конструкций для лучшего, среднего и худшего случаев.

Особенностью оценки ресурсной эффективности рекурсивных алгоритмов является необходимость учета дополнительных затрат памяти и механизма организации рекурсии. Поэтому трудоемкость рекурсивных реализаций алгоритмов связана с количеством операций, выполняемых при оном рекурсивном вызове, а также с количеством таких вызовов. Учитываются также затраты на возвращения значений и передачу управления в точку вызова. Для анализа трудоемкости механизма рекурсивного вызова-возврата будем учитывать следующие параметры: p – количество передаваемых фактических параметров, r – количество сохраняемых в стеке регистров, k – количество возвращаемых по адресной ссылке значений, l – количество локальных ячеек функции. Тогда функция трудоемкости на одни вызов-возврат примет вид:

,

где дополнительная единица учитывает операции с адресом возврата.

Оценка требуемой памяти стека может быть получена следующим образом: так как рекурсивные вызовы обрабатываются последовательно, то в конкретный момент времени в стеке хранится не фрагмент дерева рекурсии, а цепочка рекурсивных вызовов – унарный фрагмент дерева. Поэтому объем стека определяется максимально возможным числом одновременно полученных рекурсивных вызовов.

Анализ совокупной трудоемкости рекурсивного алгоритма можно выполнять разными способами в зависимости от формирования итоговой суммы базовых операций: по цепочкам рекурсивных вызовов и возвратов, по вершинам рекурсивного дерева.

Пример 1. Оценка временной сложности функции пузырьковой сортировки.

//Описание функции сортировки методом "пузырька"

void BubbleSort (int k,int x[max]) {

int i,j,buf;

for (i=k-1;i>0;i--)

for (j=0;j<i;j++)

if (x[j]>x[j+1]) {

buf=x[j];

x[j]=x[j+1];

x[j+1]=buf;

}

}

Оценим временную сложность функции пузырьковой сортировки в худшем случае, т.е. когда исходные данные отсортированы в обратном порядке. В этом случае внутренний цикл для каждого i выполнится i -1 раз и произойдет обменов. Соответственно сложность алгоритма в худшем случае составит обменов.

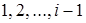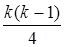Оценим временную сложность алгоритма пузырьковой сортировки в среднем случае, т.е. когда исходные данные имеют произвольный порядок. В этом случае условие во внутреннем цикле может выполниться раз. Складывая, получим и, соответственно, условие во внутреннем цикле для каждого i выполнится в среднем раз и произойдет обменов. Соответственно сложность алгоритма в среднем случае составит .

Пример 2. Оценка временной сложности функции вычисления биномиального коэффициента .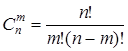

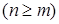//Описание функции вычисления биномиального коэффициента

int Binom (int n,int m) {

if (m==0) return 1; //база рекурсии

return Binom(n-1,m-1)*n/m; //декомпозиция

}

Оценим временную сложность функции в худшем случае, т.е. когда m=n. Будет выполнено (n +1) обращений к функции, которая выполнит в n случаях три операции, а в одном возвратит значение. Функция при каждом обращении передает два параметра, не использует локальных переменных, а при возвращении (n +1) раз передает управление в точку вызова. Соответственно сложность алгоритма в худшем случае составит или .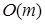

Оценим временную сложность функции в среднем случае, т.е. когда m<n. При этом выполняются рассуждения, аналогичные худшему случаю, только количество рекурсивных вызовов составит (m +1). Соответственно сложность алгоритма в среднем случае составит .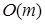

Лучший случай достигается при m =0, когда выполняется единственный вызов функции, передача двух параметров и возвращение в точку вызова, то есть оценка лучшего случая .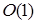

Дата добавления: 2014-01-04