Бинарный (двоичный) поиск

Бинарный (двоичный, дихотомический) поиск – это поиск заданного элемента на упорядоченном множестве, осуществляемый путем неоднократного деления этого множества на две части таким образом, что искомый элемент попадает в одну из этих частей. Поиск заканчивается при совпадении искомого элемента с элементом, который является границей между частями множества или при отсутствии искомого элемента.

Бинарный поиск применяется к отсортированным множествам и заключается в последовательном разбиении множества пополам и поиска элемента только в одной половине на каждой итерации.

Таким образом, идея этого метода заключается в следующем. Поиск нужного значения среди элементов упорядоченного массива (по возрастанию или по убыванию) начинается с определения значения центрального элемента этого массива. Значение данного элемента сравнивается с искомым значением и в зависимости от результатов сравнения предпринимаются определенные действия. Если искомое и центральное значения оказываются равны, то поиск завершается успешно. Если искомое значение меньше центрального или больше, то формируется массив, состоящий из элементов, находящихся слева или справа от центрального соответственно. Затем поиск повторяется в новом массиве (рис. 1).

Алгоритм бинарного поиска

Шаг 1. Определить номер среднего элемента массива .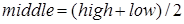

Шаг 2. Если значение среднего элемента массива равно искомому, то возвращаем значение, равное номеру искомого элемента, и алгоритм завершает работу.

Шаг 3. Если искомое значение больше значения среднего элемента, то возьмем в качестве массива все элементы справа от среднего, иначе возьмем в качестве массива все элементы слева от среднего (в зависимости от характера упорядоченности). Перейдем к Шагу 1.

В массиве может встречаться несколько элементов со значениями, равными ключу. Данный алгоритм находит первый совпавший с ключом элемент, который в порядке следования в массиве может быть ни первым, ни последним среди равных ключу. Например, в массиве чисел 1, 5, 5, 5, 5, 5, 5, 7, 8 с ключом key =5 совпадет элемент с порядковым номером 4, который не относится ни к первому, ни к последнему.

Существуют две модификации рассматриваемого алгоритма для поиска первого и последнего вхождения. Все зависит от того, как выбирается средний элемент: округлением в меньшую или большую сторону. В первом случае средний элемент относится к левой части массива, а во втором – к правой.

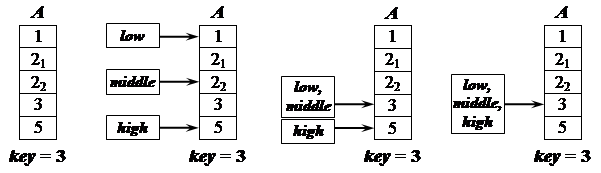Рис.1. Демонстрация алгоритма бинарного поиска

//описание функции бинарного поиска

int BinarySearch(int *x, int k, int key){

bool found = false;

int high = k - 1, low = 0;

int middle = (high + low) / 2;

while (!found && high >= low){

if (key == x[middle])

found = true;

else if (key < x[middle])

high = middle - 1;

else

low = middle + 1;

middle = (high + low) / 2;

}

return found? middle: -1;

}

В процессе работы алгоритма бинарного поиска размер фрагмента, где этот поиск должен продолжаться, каждый раз уменьшается примерно в два раза. Это обеспечивает сложность алгоритма пропорциональную 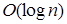, где n – количество элементов множества.

Время выполнения алгоритма бинарного поиска: если функция имеет вещественный аргумент, найти решение с точностью до 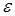можно за время 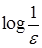, а если аргумент дискретен, то поиск решения займет времени.

Достоинством данного алгоритма является относительная быстрота выполнения поиска, по сравнению с алгоритмом последовательного поиска. Недостаток заключается в том, что бинарный поиск может применяться только на упорядоченном множестве.

Дата добавления: 2014-01-04