Двоичные упорядоченные деревья

Двоичное дерево упорядоченно, если для любой его вершины x справедливы такие свойства (рис. 1):

· все элементы в левом поддереве меньше элемента, хранимого в x,

· все элементы в правом поддереве больше элемента, хранимого в x,

· все элементы дерева различны.

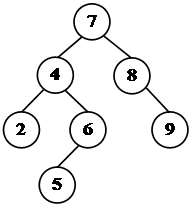Рис. 1. Двоичное упорядоченное дерево

Если в дереве выполняются первые два свойства, но встречаются одинаковые элементы, то такое дерево является частично упорядоченным. В дальнейшем будет идти речь только о двоичных упорядоченных деревьях. Основными операциями, производимыми с упорядоченным деревом, являются:

· поиск вершины;

· добавление вершины;

· удаление вершины;

· вывод (печать) дерева;

· очистка дерева.

Пример 1. Программная реализация основных операций бинарного дерева поиска.

#include "stdafx.h"

#include <iostream>

#include <time.h>

using namespace std;

typedef int T; // тип элемента

#define compLT(a,b) (a < b)

#define compEQ(a,b) (a == b)

typedef struct Node_ {

T data; // значение узла

struct Node_ *left;// левый потомок

struct Node_ *right;// правый потомок

struct Node_ *parent;// родитель

} Node;

Node *root = NULL; //корень бинарного дерева поиска

Node* insertNode(T data);

void deleteNode(Node *z);

Node* findNode(T data);

void printTree(Node *node, int l = 0);

int _tmain(int argc, _TCHAR* argv[]){

int i, *a, maxnum;

cout << "Введите количество элементов maxnum: ";

cin >> maxnum;

cout << endl;

a = new int[maxnum];

srand(time(NULL)*1000);

// генерация массива

for (i = 0; i < maxnum; i++)

a[i] = rand();

cout << "Вывод сгенерированной последовательности" << endl;

for (i = 0; i < maxnum; i++)

cout << a[i] << " ";

cout << endl;

cout << endl;

// добавление элементов в бинарное дерево поиска

for (i = 0; i < maxnum; i++) {

insertNode(a[i]);

}

cout << "Вывод бинарного дерева поиска" << endl;

printTree(root);

cout << endl;

// поиск элементов по бинарному дереву поиска

for (i = maxnum-1; i >= 0; i--) {

findNode(a[i]);

}

// очистка бинарного дерева поиска

for (i = 0; i < maxnum; i++) {

deleteNode(findNode(a[i]));

}

system("pause");

return 0;

}

//функция выделения памяти для нового узла и вставка в дерево

Node* insertNode(T data) {

Node *x, *current, *parent;

current = root;

parent = 0;

while (current) {

if (data == current->data) return (current);

parent = current;

current = data < current->data?

current->left: current->right;

}

x = new Node;

x->data = data;

x->parent = parent;

x->left = NULL;

x->right = NULL;

if(parent)

if(x->data < parent->data)

parent->left = x;

else

parent->right = x;

else

root = x;

return(x);

}

//функция удаления узла из дерева

void deleteNode(Node *z) {

Node *x, *y;

if (!z || z == NULL) return;

if (z->left == NULL || z->right == NULL)

y = z;

else {

y = z->right;

while (y->left!= NULL) y = y->left;

}

if (y->left!= NULL)

x = y->left;

else

x = y->right;

if (x) x->parent = y->parent;

if (y->parent)

if (y == y->parent->left)

y->parent->left = x;

else

y->parent->right = x;

else

root = x;

if (y!= z) {

y->left = z->left;

if (y->left) y->left->parent = y;

y->right = z->right;

if (y->right) y->right->parent = y;

y->parent = z->parent;

if (z->parent)

if (z == z->parent->left)

z->parent->left = y;

else

z->parent->right = y;

else

root = y;

free (z);

}

else {

free (y);

}

}

//функция поиска узла, содержащего data

Node* findNode(T data) {

Node *current = root;

while(current!= NULL)

if(compEQ(data, current->data))

return (current);

else

current = compLT(data, current->data)?

current->left: current->right;

return(0);

}

//функция вывода бинарного дерева поиска

void printTree(Node *node, int l){

int i;

if (node!= NULL) {

printTree(node->right, l+1);

for (i=0; i < l; i++) cout << " ";

printf ("%4ld", node->data);

printTree(node->left, l+1);

}

else cout << endl;

}

Алгоритм удаления элемента более трудоемкий, так как надо соблюдать упорядоченность дерева. При удалении может случиться, что удаляемый элемент находится не в листе, то есть вершина имеет ссылки на реально существующие поддеревья. Эти поддеревья терять нельзя, а присоединить два поддерева на одно освободившееся после удаления место невозможно. Поэтому необходимо поместить на освободившееся место либо самый правый элемент из левого поддерева, либо самый левый из правого поддерева. Упорядоченность дерева при этом не нарушится. Удобно придерживаться одной стратегии, например, заменять самый левый элемент из правого поддерева. Нельзя забывать, что при замене вершина, на которую производится замена, может иметь правое поддерево. Это поддерево необходимо поставить вместо перемещаемой вершины.

Временная сложность этих алгоритмов (она одинакова для этих алгоритмов, так как в их основе лежит поиск) оценим для наилучшего и наихудшего случая. В лучшем случае, то есть случае полного двоичного дерева, получаем сложность 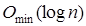. В худшем случае дерево может выродиться в список. Такое может произойти, например, при добавлении элементов в порядке возрастания. При работе со списком в среднем придется просмотреть половину списка. Это даст сложность .

Дата добавления: 2014-01-04