Сортировка слиянием

Алгоритм сортировки слиянием был изобретен Джоном фон Нейманом в 1945 году. Он является одним из самых быстрых способов сортировки.

Слияние – это объединение двух или более упорядоченных массивов в один упорядоченный.

Сортировка слиянием является одним из самых простых алгоритмов сортировки (среди быстрых алгоритмов). Особенностью этого алгоритма является то, что он работает с элементами массива преимущественно последовательно, благодаря чему именно этот алгоритм используется при сортировке в системах с различными аппаратными ограничениями (например, при сортировке данных на жестком диске). Кроме того, сортировка слиянием является алгоритмом, который может быть эффективно использован для сортировки таких структур данных, как связанные списки.

Данный алгоритм применяется тогда, когда есть возможность использовать для хранения промежуточных результатов память, сравнимую с размером исходного массива. Он построен на принципе «разделяй и властвуй». Сначала задача разбивается на несколько подзадач меньшего размера. Затем эти задачи решаются с помощью рекурсивного вызова или непосредственно, если их размер достаточно мал. Далее их решения комбинируются, и получается решение исходной задачи (рис. 4).

Процедура слияния требует два отсортированных массива. Заметим, что массив из одного элемента по определению является отсортированным.

Алгоритм сортировки слиянием

Шаг 1. Разбить имеющиеся элементы массива на пары и осуществить слияние элементов каждой пары, получив отсортированные цепочки длины 2 (кроме, быть может, одного элемента, для которого не нашлось пары).

Шаг 2. Разбить имеющиеся отсортированные цепочки на пары, и осуществить слияние цепочек каждой пары.

Шаг 3. Если число отсортированных цепочек больше единицы, перейти к шагу 2.

Рис.4. Демонстрация сортировки слиянием по неубыванию

//Описание функции сортировки слиянием

void Merging_Sort (int n, int *x){

int i, j, k, t, s, Fin1, Fin2;

int* tmp = new int[n];

k = 1;

while (k < n){

t = 0;

s = 0;

while (t+k < n){

Fin1 = t+k;

Fin2 = (t+2*k < n? t+2*k: n);

i = t;

j = Fin1;

for (; i < Fin1 && j < Fin2; s++){

if (x[i] < x[j]) {

tmp[s] = x[i];

i++;

}

else {

tmp[s] = x[j];

j++;

}

}

for (; i < Fin1; i++, s++)

tmp[s] = x[i];

for (; j < Fin2; j++, s++)

tmp[s] = x[j];

t = Fin2;

}

k *= 2;

for (s = 0; s < t; s++)

x[s] = tmp[s];

}

delete(tmp);

}

Недостаток алгоритма заключается в том, что он требует дополнительную память размером порядка n (для хранения вспомогательного массива). Кроме того, он не гарантирует сохранение порядка элементов с одинаковыми значениями. Но его временная сложность всегда пропорциональна .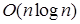

Дата добавления: 2014-01-04