Сортировка естественным слиянием

В случае простого слияния частичная упорядоченность сортируемых данных не дает никакого преимущества. Это объясняется тем, что на каждом проходе сливаются серии фиксированной длины. При естественном слиянии длина серий не ограничивается, а определяется количеством элементов в уже упорядоченных подпоследовательностях, выделяемых на каждом проходе.

Сортировка, при которой всегда сливаются две самые длинные из возможных последовательностей, является естественным слиянием. В данной сортировке объединяются серии максимальной длины.

Алгоритм сортировки естественным слиянием

Шаг 1. Исходный файл f разбивается на два вспомогательных файла f1 и f2. Распределение происходит следующим образом: поочередно считываются записи 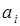исходной последовательности (неупорядоченной) таким образом, что если значения ключей соседних записей удовлетворяют условию 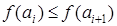, то они записываются в первый вспомогательный файл f1. Как только встречаются , то записи 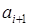копируются во второй вспомогательный файл f2. Процедура повторяется до тех пор, пока все записи исходной последовательности не будут распределены по файлам.

Шаг 2. Вспомогательные файлы f1 и f2 сливаются в файл f, при этом серии образуют упорядоченные последовательности.

Шаг 3. Полученный файл f вновь обрабатывается, как указано в шагах 1 и 2.

Шаг 4. Повторяя шаги, сливаем упорядоченные серии до тех пор, пока не будет упорядочен целиком весь файл.

Символ «`» обозначает признак конца серии.

Признаками конца сортировки естественным слиянием являются следующие условия:

· количество серий равно 1 (определяется на фазе слияния).

· при однофазной сортировке второй по счету вспомогательный файл после распределения серий остался пустым.

Естественное слияние, у которого после фазы распределения количество серий во вспомогательных файлах отличается друг от друга не более чем на единицу, называется сбалансированным слиянием, в противном случае – несбалансированное слияние.

Исходный файл f: 2 3 17 7 8 9 1 4 6 9 2 3 1 18
	Распределение	Слияние
1 проход	f1: 2 3 17 ` 1 4 6 9 ` 1 18   f2: 7 8 9 ` 2 3	f: 2 3 7 8 9 17 1 2 3 4 6 9 1 18
2 проход	f1: 2 3 7 8 9 17 ` 1 18   f2: 1 2 3 4 6 9 `	f: 1 2 2 3 3 4 6 7 8 9 9 17 1 18
3 проход	f1: 1 2 2 3 3 4 6 7 8 9 9 17   f2: 1 18	f: 1 1 2 2 3 3 4 6 7 8 9 9 17 18

Рис.2. Демонстрация сортировки двухпутевым двухфазным естественным слиянием

//Описание функции сортировки естественным слиянием

void Natural_Merging_Sort (char *name){

int s1, s2, a1, a2, mark;

FILE *f, *f1, *f2;

s1 = s2 = 1;

while (s1 > 0 && s2 > 0){

mark = 1;

s1 = 0;

s2 = 0;

f = fopen(name,"r");

f1 = fopen("nmsort_1","w");

f2 = fopen("nmsort_2","w");

fscanf(f,"%d",&a1);

if (!feof(f)) {

fprintf(f1,"%d ",a1);

}

if (!feof(f)) fscanf(f,"%d",&a2);

while (!feof(f)){

if (a2 < a1) {

switch (mark) {

case 1:{fprintf(f1,"' "); mark = 2; s1++; break;}

case 2:{fprintf(f2,"' "); mark = 1; s2++; break;}

}

}

if (mark == 1) { fprintf(f1,"%d ",a2); s1++; }

else { fprintf(f2,"%d ",a2); s2++;}

a1 = a2;

fscanf(f,"%d",&a2);

}

if (s2 > 0 && mark == 2) { fprintf(f2,"'");}

if (s1 > 0 && mark == 1) { fprintf(f1,"'");}

fclose(f2);

fclose(f1);

fclose(f);

cout << endl;

Print_File(name);

Print_File("nmsort_1");

Print_File("nmsort_2");

cout << endl;

f = fopen(name,"w");

f1 = fopen("nmsort_1","r");

f2 = fopen("nmsort_2","r");

if (!feof(f1)) fscanf(f1,"%d",&a1);

if (!feof(f2)) fscanf(f2,"%d",&a2);

bool file1, file2;

while (!feof(f1) &&!feof(f2)){

file1 = file2 = false;

while (!file1 &&!file2) {

if (a1 <= a2) {

fprintf(f,"%d ",a1);

file1 = End_Range(f1);

fscanf(f1,"%d",&a1);

}

else {

fprintf(f,"%d ",a2);

file2 = End_Range(f2);

fscanf(f2,"%d",&a2);

}

}

while (!file1) {

fprintf(f,"%d ",a1);

file1 = End_Range(f1);

fscanf(f1,"%d",&a1);

}

while (!file2) {

fprintf(f,"%d ",a2);

file2 = End_Range(f2);

fscanf(f2,"%d",&a2);

}

}

file1 = file2 = false;

while (!file1 &&!feof(f1)) {

fprintf(f,"%d ",a1);

file1 = End_Range(f1);

fscanf(f1,"%d",&a1);

}

while (!file2 &&!feof(f2)) {

fprintf(f,"%d ",a2);

file2 = End_Range(f2);

fscanf(f2,"%d",&a2);

}

fclose(f2);

fclose(f1);

fclose(f);

}

remove("nmsort_1");

remove("nmsort_2");

}

//определение конца блока

bool End_Range (FILE * f){

int tmp;

tmp = fgetc(f);

tmp = fgetc(f);

if (tmp!= '\'') fseek(f,-2,1);

else fseek(f,1,1);

return tmp == '\''? true: false;

}

Таким образом, число чтений или перезаписей файлов при использовании метода естественного слияния будет не хуже, чем при применении метода простого слияния, а в среднем – даже лучше. Но в этом методе увеличивается число сравнений за счет тех, которые требуются для распознавания концов серий. Помимо этого, максимальный размер вспомогательных файлов может быть близок к размеру исходного файла, так как длина серий может быть произвольной.

Дата добавления: 2014-01-04