Собственные и вынужденные колебания

Собственные колебания

Это колебания, вызываемые единичными импульсами (единичной неровностью) и имеющие определенную частоту.

Основными характеристиками собственных колебаний являются - частота собственных колебаний (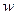) и коэффициент относительного затухания (к).

Автомобиль имеет количество частот собственных колебаний по количеству степеней свободы. То есть он имеет определенные частоты собственных вертикальных, поперечных, продольно- угловых и других колебаний.

Значения этих частот зависят от массовых и геометрических параметров автомобиля, а также от жестокости его подвески.

Так, частота собственных вертикальных колебаний двухосного автомобиля определяется по формуле: (1)

где 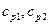- радиальная жесткость передней и задней подвески, соответственно;

- подрессоренная масса автомобиля.

Частота собственных продольно угловых колебаний определяется по формуле

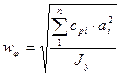, (2)

где 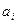- расстояние от передней и задней оси до центра тяжести автомобиля соответственно;

- момент инерции подрессоренной массы относительно оси.

Из теории колебаний известно, что чем меньше частота собственных колебаний, тем лучше плавность хода.

Но снижение жесткости подвески приводит к увеличению статистического () и динамического (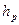) хода подвески, что приводит к усложнению конструкции подвески; значительному изменению дорожного просвета при колебаниях корпуса; увеличению амплитуды колебаний корпуса, в продольной и поперечной плоскостях.

Статистический ход подвески можно определить по формуле

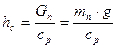(3)

где - вес подрессоренных частей

g - ускорения свободного падения (g = 9,81 м/c²) c учетом выражения (3) имеется следующая связь между частотой собственных колебаний и статическим ходом подвески

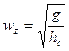(4)

Отношение величины динамического хода подвески к статистическому называется коэффициентом динамичности подвески (j)

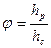(5)

Таким образом, подвеску желательно иметь более мягкую, чтобы улучшить показатели плавности хода и более жесткую, чтобы уменьшить амплитуды колебаний корпуса автомобиля. Исходя из этого, для выполненных конструкций грузовых автомобилей жесткость подвесок равна

С_р = 20…60 кН/м (200…800 кг/см)

При этом значения h_c, h_p автомобилей многоцелевого назначения представлены в таблице 1.

Таблица 1.

Марка ав-ля	Передняя подвеска	Задняя подвеска	Дор. просв.
hc	hp	j	hc	hp	j
ГАЗ- 66			0,955			1,06
ЗИЛ- 131			1,03			2,03
Урал-4320			0,915			1,63

Иногда при выборе жесткости подвесок пользуются парциальными частотами собственных колебаний, при этом подрессоренная масса (m_n) рассматривается в виде двух масс, сосредоточенных над осями (рис.2).

Парциальными частотами называются частоты колебаний с одной степенью свободы (рис.3).

Парциальные частоты вертикальных колебаний определяются по формулам

, (6)

а , тогда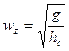

При выборе жесткости подвесок важно чтобы центр упругости совпадал с центром тяжести, в этом случае при движении по неровностям автомобиль будет иметь лишь вертикальные перемещения подрессоренных масс. Ц.У. - центр упругости, а Ц.Т. - центр тяжести автомобиля.

Рис.2.

Рис. 3.

Для современных грузовых автомобилей значения парциальных частот находятся в пределах 1,2....1,8 Гц (75...110 мин^-1).

Зная распределение масс автомобиля по осям можно рассчитать необходимую жесткость подвески.

Собственные колебания автомобиля являются затухающими, поскольку происходит рассеивание энергии:

- в амортизаторах;

- на трение в элементах подвески.

Главный источник затухания - амортизатор.

Сопротивление амортизаторов можно в первом приближении считать пропорциональным скорости перемещения подрессоренной массы относительно неподрессоренной. Следовательно, при наличии в подвесках гидравлических амортизаторов колебания будут затухать по геометрической прогрессии.

Интенсивность гашения колебаний оценивается декрементом затухания (Д₃), который равен отношению амплитуд колебаний (Z) через период (T)

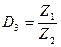(8)

Рис. 4.

На практике пользуются не декрементом затухания, а логарифмическим декрементом, который равен

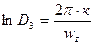(9)

где - коэффициент затухания колебаний.

Значение находится в пределах 1,5...2,0 рад/с. Чтобы учесть совместное влияние коэффициента затухания () и жесткости подвески (с_р) на частоту собственных колебаний пользуются коэффициентом апериодичности (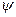), который равен

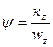(10)

У современных автомобилей 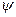= 0,15 - 0,25.

Амортизаторы выбирают с коэффициентом сопротивления, способным гасить колебания от единичной неровности за 1...2 года.

ЛЕКЦИЯ 24

Вынужденные колебания

При движении на автомобиль через его колеса действуют переменные по величине силы со стороны поверхности дороги.

Колебания автомобиля под действием переменных сил называются вынужденными.

Источниками возникновения вынужденных колебаний являются:

- взаимодействие колес с неровностями дороги (основной источник);

- геометрическая и силовая неоднородность шин;

- неравномерность вращения шин.

Неровности дороги характеризуются формой, размерами и характером чередования. Форма неровности может быть любой: синусоидальной, параболической, прямоугольной и т.д.

Размеры неровностей определяются их длиной и высотой.

По характеру чередования неровности бывают: единичные, периодически чередующиеся и случайный микропрофиль.

Высота и профиль неровностей определяют величину (амплитуду) импульсов колебаний, причем каждая неровность передает на автомобиль не один, а серию импульсов, воздействующих последовательно на каждое колесо. следовательно, в зависимости от расстановки осей по базе в одних и тех же условиях эти импульсы могут для одного автомобиля усиливать колебательный процесс, для других - ослаблять его.

Характер вынужденных колебаний зависит также от скорости движения автомобиля, так как от скорости проезда неровностей зависит частота импульсов, воздействующих на колеса.

Наиболее сложным для исследования вынужденных колебаний является случай движения по случайному микро профилю, так как случайное изменение высоты неровности по длине пути может быть охарактеризовано лишь статистически.

Оценить показатели плавности хода на дороге со случайным характером изменения микропрофиля довольно сложно.

С другой стороны, любые неровности дороги можно представить себе как совокупность чередующихся выступов и впадин, имеющих различные значения по высоте (глубине) и длине.

Рис.5.

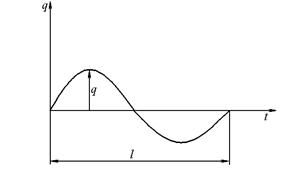
Следовательно, любую дорогу в первом приближении можно считать имеющий синусоидальный профиль с различными значениями высоты (q) и длины волны (l) неровности (рис.5).

Наиболее близкий к синусоидальному имеют профиль наезженные грунтовые дороги. Высота неровности на этих дорогах колеблется в пределах 20...200 мм, длина волны неровности - 0,5...13,0 м.

Наиболее распространены неровности высотой около 50 мм и длиной волны 4,0 м.

Для теоретического исследования вынужденных колебаний и для проведения сравнительных испытаний на плавность хода неровности дороги принимают синусоидального профиля с интервалом высоты (q = 50; 100; 150 и 200 м).

Длина волны неровности (l) может выбираться в зависимости от скорости движения автомобиля. В этом случае частоты вынужденных вертикальных колебаний, вызываемые импульсами от неровностей дороги, равны

(11)

где V - скорость движения автомобиля.

При совпадении частот вынужденных и собственных колебаний возникает явление резонанса. При этом амплитуды колебаний можно определить длину волны неровности, вызывающую резонанс при данной скорости движения, а также резонансную скорость движения на дороге с данной длиной волны

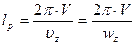(12)

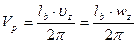(13)

где 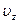- частота вынужденных вертикальных колебаний.

Дата добавления: 2014-01-04