Контрольные испытания

Контрольным испытаниям обычно подвергаются подсистемы, технические средства и их элементы. Так, для технических средств, входящих в состав ГСП, обязательными являются контрольные испытания на безотказность. Испытания на ремонтопригодность, сохраняемость и долговечность проводят в тех случаях, когда это предусмотрено стандартами, тёхническими заданиями или техническими условиями на конкретный прибор (средства). Периодичность контрольных испытаний на безотказность обычно не реже одного раза в три года.

Для проведения контрольных испытаний из совокупности (партии) однородных приборов составляется некоторая выборка и проводятся испы­тания на надежность попавших в эту выборку приборов. По результатам испытания выборки выносится суждение о соответствии всей партии предъявляемым требованиям.

Математический аппарат решения этой задачи — изучаемые в матема­тической статистике методы проверки статистических гипотез. В качест­ве проверяемой (или, как принято говорить, нулевой) гипотезы принима­ется предположение, что партия соответствует требованиям к надежно­сти, в качестве противоположной (альтернативной) – что партия не удовлетворяет этим требованиям.

По результатам испытаний имеет место одна из следующих четырех ситуаций:

1. Партия удовлетворяет требованиям; по результатам испытаний подтвердилась нулевая гипотеза и принято решение о принятии партии. Это решение правильно.

2. Партия удовлетворяет требованиям, но по результатам испытаний нуле­вая гипотеза не подтвердилась. Это произошло потому, что случайно составленная выборка содержала повышенное число отказавших приборов по срав­нению с совокупностью. Принята альтернативная гипотеза; это решение не­правильно и невыгодно для изготовителя приборов. При этом произошла ошибка, вероятность которой называют риском поставщика (изготовителя) α.

3. Партия не удовлетворяет требованиям, по результатам испытаний нуле­вая гипотеза не подтвердилась. Принята альтернативная гипотеза, т. е. реше­ние о непринятии партии. Это решение правильно.

4. Партия не удовлетворяет требованиям, но по результатам испытаний подтвердилась нулевая гипотеза о соответствии требованиям к надежности, так как выборка содержала повышенное число неотказавших приборов по сравнению со всей партией. Принято неправильное решение, но оно невыгод­но в отличие от п. 2 не изготовителю, а потребителю – заказчику этих при­боров. Произошла ошибка, вероятность которой называют риском потреби­теля (заказчика) β.

Естественно, что желательно снизить значения обеих ошибок, доведя их в пределе до нуля. Зависимость вероятности L приемки партии от показателя надежности А (называемая оперативной характеристикой плана контроля) для такой предельной ситуации дана на рис. 4.3, а. Пусть А_тр – требуемое значе­ние показателя надежности. В этой ситуации нулевая гипотеза А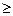А_тр. Если она справедлива, то партия принимается с вероятностью, равной единице, причем α= 0. Альтернативная гипотеза заключается в том, что А<А_тр. При этом партия бракуется с вероятностью, равной единице, причем β= 0. Однако такая идеальная оперативная характеристика недостижима, так как требует бесконечного объема наблюдений.

В реальной ситуации вводятся два уровня контролируемого показателя на­дежности: приемочный А_α и браковочный А_β (рис. 4.3,б). Если А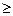А_α, то при­боры должны приниматься с достаточно высокой вероятностью, не ниже L(А_α), если А<А_β, то приборы должны браковаться с достаточно высокой вероятностью, не ниже 1 –L(А_β). При этом риск поставщика α= 1 -L(А_α), риск потребителя α= 1 -L(А_α). Тем самым проверку нулевой гипотезы А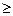А_тр при аль­тернативе А<А_тр заменяем другой задачей — проверкой нулевой гипотезы А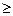А_α при альтернативе А<А_β. Чем ближе А_α к А_β, тем больший объем испы­таний необходим для принятия достоверного решения о соответствии партии.

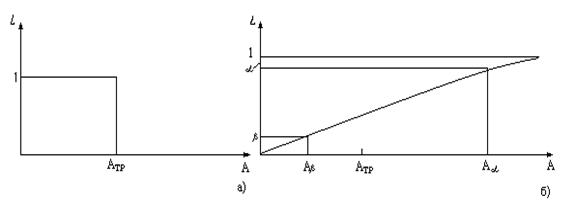
Рис. 4.3 Идеальная (а) и реальная (б) оперативные характеристики планов контроля

Практически в качестве приемочного уровня А_α принимают: расчетное значение показателя надежности, если не было испытаний надежности; худ­шую доверительную границу показателя надежности (А_н или А_вр), если про­водились определительные испытания.

Значение браковочного уровня А_β устанавливается с учетом приемочно­го уровня А_α, стоимости, продолжительности и условий испытаний и т. п.

Риск поставщика α и потребителя β обычно принимается равным 0,1-0,2, но в принципе по согласованию между потребителем и поставщиком воз­можен выбор и иных значений α и β.

Контрольные испытания на безотказность проводятся обычно одно- или двухступенчатым методом. При применении первого из них испытания выполняют следующим образом. Образцы, вошедшие в выборку объема d, испытывают в течение времени t_И. По окончании испытаний определяют число наступивших отказов п. Если оно равно или меньше приемочного числа отказов с, определенного в зависимости от величин А_α, А_β, α и β, то нулевая гипотеза подтверждается и партию принимают. Если же п>с, то подтверждается альтернативная гипотеза и партию не принимают.

При применении двухступенчатого метода определяют объемы выборок n ₁ и n ₂ и приемочные числа отказов c ₁ и c ₂ для первой и второй ступеней, зависящие от величин А_α, А_β, α и β.

Образцы, вошедшие в первую выборку, испытывают в течение времени t_и и определяют число наступивших отказов d ₁. Если , то результаты контрольных испытаний положительны. Если 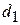> c₁ + c₂, то испытания прекращаются, а их результаты считаются отрицательными. Если c ₁ < d ₁ 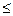c ₁ + c ₂, то проводят испытания второй ступени.

Образцы изделий, вошедшие во вторую выборку, также испытывают в течение времени t ₁. По окончании второй ступени определяют суммарное число отказов d ₁ + d ₂. Если 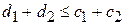, то результаты испытаний положительны; если 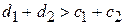, то отрицательны.

Одноступенчатый метод при прочих равных условиях обеспечивает ми­нимальную календарную продолжительность испытаний, двухступенчатый при тех же условиях позволяет обеспечить минимум среднего объема ис­пытаний.

Дата добавления: 2014-01-04