Ланцюги Маркова та їх основні характеристики

Марковський випадковий процес з дискретними станами та дискретним часом називається ланцюгом Маркова.

Як уже відзначалося, для такого процесу моменти часу коли система може змінювати свій стан, розглядають як послідовні кроки процесу, а в якості аргумента, від якого залежить процес, виступає не час 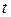, а номер кроку . Випадковий процес у цьому випадку характеризується послідовністю станів 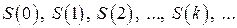, де – початковий стан системи (перед першим кроком), 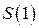– стан системи після першого кроку, 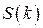– стан системи після -го кроку,....

Якщо через 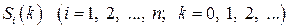позначити подію, яка полягає в тому, що відразу після -го кроку система знаходиться в стані 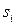, тобто 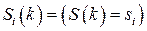, то випадковий процес з дискретним часом можна розглядати як випадкову послідовність (за індексом ) цих подій 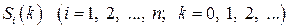, яку називають також ланцюгом.

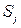Означення. Випадкова послідовність називається ланцюгом Маркова, якщо для кожного кроку ймовірність переходу з будь-якого стану в будь-який стан не залежить від того, коли і як система виявилася в стані .

Очевидно, що реалізацію дискретного випадкового процесу з дискретним часом за будь-який (скінчений) проміжок часу можна представити невипадковою скінченною послідовністю (за індексом ) розглядуваних подій 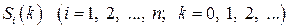. Наприклад, припустимо, що граф станів системи , в якій відбувається випадковий процес з дискретним часом, має вигляд, зображений на рис. 3. Спостереження за системою показало, що в початковий момент система знаходилася в стані 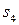; в момент першого кроку перейшла з нього стрибком у стан 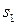, з якого на другому кроці перейшла в 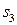, на третьому кроці перейшла в , на четвертому кроці перейшла в 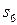, після п’ятого кроку знаходилася в стані . Тоді реалізація випадкового процесу блукання по станах має такий вигляд: .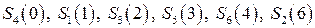

Зауваження. Для того, щоб 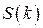при фіксованому можна було інтерпретувати як (дискретну) випадкову величину, потрібно кожний стан 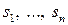охарактеризувати кількісно. Це можна зробити різними способами. Наприклад, приписати кожному стану 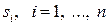в якості кількісної характеристики його номер 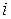, тобто 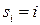. Тоді переріз випадкового процесу буде представляти дискретну випадкову величину з множиною значень . Далі, , означає подію «після -то кроку ланцюг Маркова знаходиться в стані 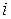», а послідовність станів, , які приймає випадковий процес 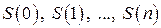визначає реалізацію або траєкторію процесу.

Враховуючи дане зауваження, більш змістовне означення ланцюга Маркова можна сформулювати так.

Означення. Послідовність випадкових величин 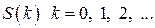, називається ланцюгом Маркова з множиною станів , якщо

і для будь-яких , будь-яких та будь-яких підмножин 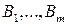множини 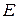виконується рівність

. (3)

Властивість (3) означає, що при фіксованому значенні системи в даний момент часу поведінка системи в майбутньому 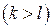не залежить від поведінки системи в минулому , або більш коротко: при фіксованому теперішньому майбутнє не залежить від минулого. Властивість (3) називають марковською властивістю.

Надалі ми будемо використовувати обидві термінології щодо інтерпретації ланцюга Маркова.

З означення ланцюга Маркова і формули (48) випливає, що ланцюг Маркова може бути заданий розподілом ймовірностей переходу за один крок.

Означення. Ймовірністю переходу (перехідною ймовірністю) на -му кроці із стану 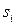в стан називається умовна ймовірність того, що система після -го кроку виявиться в стані 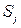за умови, що безпосередньо перед цим (після -го кроку) вона знаходилася в стані :

. (4)

Якщо множину станів позначити через , то можна трактувати як ймовірність того, що ланцюг Маркова, знаходячись після -го кроку в стані 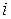, після наступного -то кроку виявиться в стані :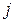

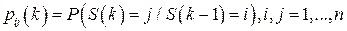(5)

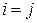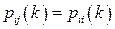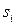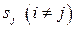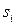У випадку, коли , то перехідна ймовірність називається ймовірністю затримки системи у стані. Якщо на -му кроці безпосередній перехід системи із стану в інший стан неможливий або неможливою є затримка в стані , то .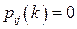

Означення. Якщо перехідні ймовірності 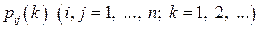не залежать від номера кроку (від часу), а залежать лише від того, з якого стану в який здійснюється перехід, то відповідний ланцюг Маркова називається однорідним.

Якщо хоча б одна ймовірність змінюється зі зміною кроку , то ланцюг Маркова називається неоднорідним. Надалі ми будемо розглядати лише однорідні ланцюги Маркова. У цьому випадку перехідні ймовірності будемо позначати через 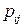замість . Сукупність ймовірностей переходу утворює матрицю

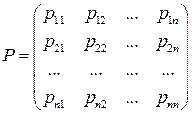, (6)

вона називається однорідною матрицею переходів (перехідних ймовірностей). За означенням всі елементи матриці 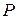невід’ємні. Крім цього, оскільки для будь-якої події , яка наступила після -го кроку, для наступного -го кроку одна з подій 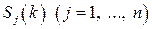обов’язково відбудеться, то елементи кожного рядка матриці 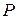задовольняють умову

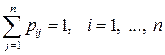. (7)

Означення. Квадратна матриця називається стохастичною, якщо її елементи невід’ємні і сума елементів будь-якого її рядка дорівнює одиниці.

Отже, матрицею переходів ланцюга Маркова зі скінченним числом станів називається стохастична матриця з порядком , елементами якої є відповідні перехідні ймовірності .

Часто також задаються ймовірності станів ланцюга Маркова на початковому нульовому кроці:

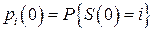або (8)

На ймовірності накладаються очевидні умови невід’ємності 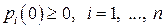і нормування:

. (9)

У частковому випадку, якщо початковий стан системи відомий і , то початкова ймовірність , а всі решта дорівнюють нулю.

За допомогою формул (3), (5) із врахуванням (8) можна обчислити ймовірність будь-якої конкретної траєкторії ланцюга Маркова:

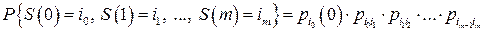. (10)

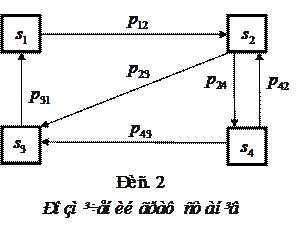Легко показати, що формула (55) задає ймовірності на просторі 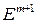всіх траєкторій довжини . Зокрема, виконується умова нормування для ймовірностей:

. (11)

Корисним зображенням ланцюга Маркова є її розмічений граф станів системи, де біля кожної стрілки, яка веде зі стану 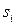в стан 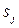(зі стану 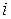в стан 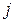) відзначена перехідна ймовірність 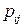. Взірець такого розміченого графа станів показано на рис. 2.

Наявність на розміченому графі стрілок і відповідних їм ймовірностей з одного стану в інший означає, що ці перехідні ймовірності відмінні від нуля. Навпаки, відсутність стрілок з одного стану в інший вказує на те, що відповідні їм перехідні ймовірності дорівнюють нулю. Наприклад, , а .

Перехідні ймовірності, які відповідають стрілкам, що виходять із станів розміщені в 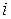-му рядку матриці 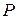перехідних ймовірностей, а тому їх сума, внаслідок (7), дорівнює одиниці. Тому ймовірності затримок 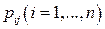можна обчислити за формулою

(12)

Внаслідок цього стрілки – петлі та відповідні їм ймовірності затримок на графі, як правило, не відзначаються.

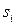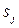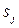Ймовірність переходу за кроків. Розглянемо ймовірність переходу із стану , який реалізований, наприклад, після -го кроку, в стан за кроків, тобто в стан після -го кроку. Зрозуміло, що внаслідок однорідності ланцюга Маркова ця ймовірність залежить тільки від (і не залежить від ). Позначимо її . Тоді 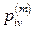– ймовірність переходу за кроків із стану 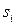в стан 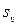та – ймовірність переходу за 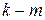кроків із стану 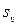в .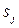

Використовуючи формулу повної ймовірності та враховуючи, що проміжні стани 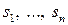на 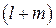– у кроці утворюють повну групу попарно несумісних подій, знайдемо

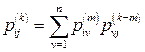, (13)

де – будь-яке ціле значення від 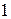до .

Позначимо через матрицю, яка складається з ймовірностей , отже – матриця переходів через кроків .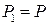

Враховуючи формулу для перемноження квадратних матриць, рівність (13) можна записати в матричному вигляді:

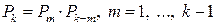. (14)

Застосовуючи послідовно (59), одержимо

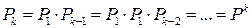, (15)

тобто для того, щоб отримати матрицю ймовірностей переходів за кроків, потрібно просто піднести до -го степеня вихідну матрицю ймовірностей переходів .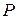

Неважко переконатися в тому, що при будь-якому натуральному матриця 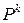є стохастичною.

Безумовна (абсолютна) ймовірність 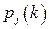того, що система після -го кроку знаходиться в стані 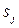, обчислюється також з використанням формули повної ймовірності:

. (16)

Простим наслідком формули (61) є наступне співвідношення

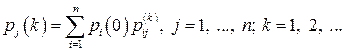. (17)

Рекурентні формули (16), (17) можна записати також у матричному вигляді. Справді, якщо абсолютні ймовірності станів визначені у векторній формі як 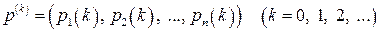, то на підставі рівностей (14) - (17) маємо

. (18)

або

. (19)

Ймовірності першого досягнення стану 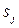при виході зі стану 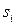. Введемо до розгляду ймовірність того, що, починаючи зі стану 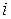, ланцюг Маркова вперше досягає стан у на -му кроці. 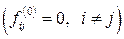, тобто

.

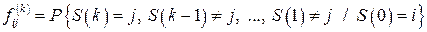Спираючись на формулу повної ймовірності, можуть бути обчислені через ймовірності 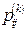внаслідок рекурентного застосування наступних формул:

(20)

За допомогою ймовірностей можна визначати значення деяких інших характеристик, які використовуються при аналізі ланцюга Маркова. Зокрема, через ці ймовірності можуть бути обчислені:

• ймовірність того, що, починаючи зі стану 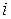, система коли-небудь потрапить в стан :

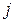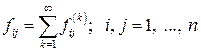; (21)

• середнє число кроків до першого досягнення стану 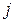при виході зі стану :

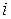. (22)

Зауваження. Для знаходження вектора в прикладі 9 можна було б замість формули (19) чотири рази послідовно використати формулу (18), а саме, спочатку за цією формулою знайти вектор ймовірностей станів у першому кварталі 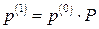, потім, у другому кварталі 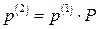і т. д., поки не дійдемо до четвертого кварталу .

Дата добавления: 2014-01-04