
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекція №11. Застосування диференціального числення для дослідження функцій
|
|
|
|
1. Монотонність функції
2. Локальний екстремум функції. Найбільше і найменшу значення функції
3. Опуклість і вгнутість функції. Точки перегину
4. Асимптоти кривої
5. Схема дослідження функції та побудова її графіка
1. Монотонність функції
Теорема 1 (достатні умови строгої монотонності)
Якщо функція  диференційовна на інтервалі
диференційовна на інтервалі  і
і  всюди, крім, можливо, скінченного числа точок, в яких
всюди, крім, можливо, скінченного числа точок, в яких 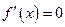 на
на  , то функція
, то функція  зростає (спадає).
зростає (спадає).
Теорема 2 (необхідна умова зростання)
Якщо диференційовна на інтервалі  функція зростає, то
функція зростає, то  на
на  .
.
Інтервали монотонності можуть відділятись один від одного або точками, де похідна дорівнює нулю (їх називають стаціонарними точками), або точками, де похідна не існує.
Точки, в яких похідна дорівнює нулю або не існує називаються критичними точками першого роду.
Правило знаходження проміжків монотонності функції  :
:
1. Знайти область визначення функції;
2. Знайти похідну функції;
3. Знайти критичні токи з рівняння 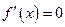 та з умови, що
та з умови, що  не існує:
не існує:
4. розділити критичними точками область визначення на інтервали та у кожному з них визначити знак похідної. На інтервалах, де похідна додатна, функція зростає, а де від’ємна – спадає.
2. Локальний екстремум функції. Найбільше і найменшу значення функції
Точка  називається точкою локального максимуму (мінімуму) функції
називається точкою локального максимуму (мінімуму) функції  , якщо існує такий окіл
, якщо існує такий окіл 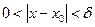 точки
точки  , який належить області визначення функції, і для всіх
, який належить області визначення функції, і для всіх 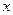 з цього околу виконується нерівність
з цього околу виконується нерівність 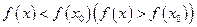 .
.
Точки локального максимуму і локального мінімуму називаються точками локального екстремуму, а значення функції в цих точках називаються відповідно локальним максимумом і локальним мінімумом або локальним екстремумом.
Абсолютний максимум (мінімум) – це найбільше (найменше) значення функції, яке вона може набувати в області визначення.
Локальних максимумів (мінімумів) функція може мати кілька, абсолютний максимум (мінімум) може бути тільки один.
Теорема 1 (необхідна умова локального екстремуму)
Якщо функція  має в точці
має в точці  локальний екстремум і диференційовна в цій точці, то
локальний екстремум і диференційовна в цій точці, то  .
.
Теорема 2 (перша достатня умова локального екстремуму)
Нехай  - критична точка функції
- критична точка функції  , яка в цій точці неперервна, і нехай існує окіл
, яка в цій точці неперервна, і нехай існує окіл 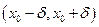 точки
точки  , в якому функція має похідну
, в якому функція має похідну  крім, можливо, точки
крім, можливо, точки  , тоді:
, тоді:
1. Якщо в інтервалі  похідна
похідна  , а в інтервалі
, а в інтервалі 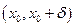 похідна
похідна  , то
, то  є точкою локального максимуму функції
є точкою локального максимуму функції  ;
;
2. Якщо в інтервалі  похідна
похідна  , а в інтервалі
, а в інтервалі 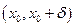 похідна
похідна  , то
, то  є точкою локального мінімуму функції
є точкою локального мінімуму функції  ;
;
3. Якщо в обох інтервалах  і
і 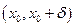 похідна
похідна  має той самий знак, то
має той самий знак, то  не є екстремальною точкою функції
не є екстремальною точкою функції  .
.
Теорема 3 (друга достатня умова локального екстремуму)
Нехай  - стаціонарна точка функції
- стаціонарна точка функції  , тобто
, тобто  , і в околі точки
, і в околі точки  існує друга неперервна похідна, причому
існує друга неперервна похідна, причому  . Якщо
. Якщо 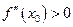 , то
, то  - точка локального мінімуму; якщо
- точка локального мінімуму; якщо  , то
, то  - точка локального максимуму.
- точка локального максимуму.
Теорема 4 (третя достатня умова локального екстремуму)
Нехай в околі стаціонарної точки  існує неперервна похідна
існує неперервна похідна  , причому
, причому  ,
,  . Тоді:
. Тоді:
1. якщо n – парне і 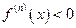 , то
, то  має в точці
має в точці  локальний максимум;
локальний максимум;
2. якщо n – парне і  , то
, то  має в точці
має в точці  локальний мінімум;
локальний мінімум;
3. якщо n – непарне, то  в точці
в точці  локального екстремуму не має.
локального екстремуму не має.
Нехай функція  неперервна на відрізку
неперервна на відрізку  . Така функція досягає своїх найбільшого і найменшого значень, які називаються абсолютними екстремумами функції на цьому відрізку і позначаються відповідно
. Така функція досягає своїх найбільшого і найменшого значень, які називаються абсолютними екстремумами функції на цьому відрізку і позначаються відповідно  .
.
Правило знаходження найбільшого (найменшого) значення функції, неперервної на відрізку  :
:
1. Знайти критичні точки функції  , які належать інтервалу
, які належать інтервалу  ;
;
2. Обчислити значення функції  у знайдених критичних точках і точках
у знайдених критичних точках і точках  та
та  і серед цих значень вибрати найбільше (найменше).
і серед цих значень вибрати найбільше (найменше).
3. Опуклість і вгнутість функції. Точки перегину
Крива 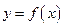 називається опуклою на інтервалі, якщо всі її точки, крім точки дотику, лежать нижче довільної її дотичної на цьому інтервалі.
називається опуклою на інтервалі, якщо всі її точки, крім точки дотику, лежать нижче довільної її дотичної на цьому інтервалі.
Крива 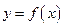 називається вгнутою на інтервалі, якщо всі її точки, крім точки дотику, лежать вище довільної її дотичної на цьому інтервалі.
називається вгнутою на інтервалі, якщо всі її точки, крім точки дотику, лежать вище довільної її дотичної на цьому інтервалі.
Точкою перегину називається така очка кривої, яка відділяє її опуклу частину від вгнутої.

Теорема 1 (знаходження інтервалів опуклості і вгнутості)
Нехай функція 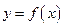 є двічі диференційовною на
є двічі диференційовною на  , тоді:
, тоді:
1. якщо 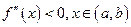 , то крива
, то крива 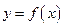 опукла на
опукла на  ;
;
2. якщо  , то крива
, то крива 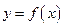 вгнута на
вгнута на  .
.
Наслідок. В точці перегину друга похідна дорівнює нулю (якщо вона існує).
Точки, в яких друга похідна дорівнює нулю або не існує, називаються критичними точками другого роду.
Теорема 2 (достатні умови існування точки розриву)
Нехай  - критична точка другого роду функції
- критична точка другого роду функції  . Якщо при переході через точку
. Якщо при переході через точку  похідна
похідна  змінює знак, то точка
змінює знак, то точка  є точкою перегину кривої
є точкою перегину кривої  .
.
Наслідок. Щоб знайти точки перегину кривої треба знайти критичні точки другого роду і дослідити зміну знака другої похідної при переході через ці точки.
4. Асимптоти кривої
Пряма 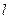 називається асимптотою кривої, якщо відстань від змінної точки
називається асимптотою кривої, якщо відстань від змінної точки 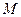 кривої до цієї прямої прямує до нуля, коли точка
кривої до цієї прямої прямує до нуля, коли точка 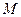 , рухаючись по кривій, віддаляється на нескінченність.
, рухаючись по кривій, віддаляється на нескінченність.
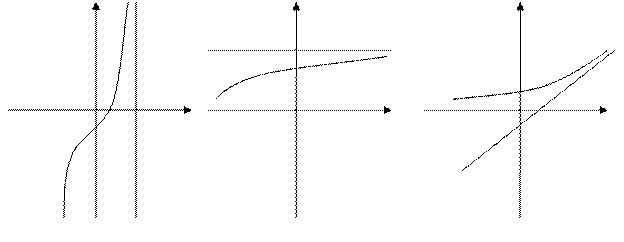
вертикальна горизонтальна похила
асимптота асимптота асимптота
Для існування вертикальної асимптоти 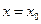 необхідно і достатньо, щоб
необхідно і достатньо, щоб 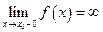 , або
, або  , або
, або  .
.
Рівняння похилої асимптоти 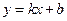 , де
, де 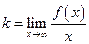 (1),
(1), 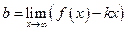 (2).
(2).
Зауваження 1. Якщо хоча б одна з границь (1) або (2) не існує, або дорівнює нескінченності, то крива похилої асимптоти не має.
Зауваження 2. Якщо  , то
, то 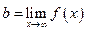 , тому
, тому  – рівняння горизонтальної асимптоти.
– рівняння горизонтальної асимптоти.
Зауваження 3. Асимптоти кривої 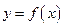 при
при 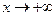 і
і 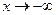 можуть бути різні. Тому при знаходженні асимптот границі (1) і (2) потрібно обчислювати при
можуть бути різні. Тому при знаходженні асимптот границі (1) і (2) потрібно обчислювати при 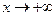 і
і 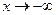 .
.
5. Схема дослідження функції та побудова її графіка
1. Знайти область існування функції;
2. Знайти (якщо це можна) точки перетину графіка з координатними осями;
3. дослідити функцію на періодичність, парність і непарність;
4. знайти точки розриву і дослідити їх;
5. знайти інтервали монотонності, точки локальних екстремумів та значення функції в цих точках;
6. знайти інтервали опуклості, вгнутості та точки перегину;
7. знайти асимптоти кривої;
8. побудувати графік функції.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 2133; Нарушение авторских прав?; Мы поможем в написании вашей работы!