Л е к ц и и № 21-23. К о л е б а т е л ь н ы е п р о ц е с с ы

Течение вязкой жидкости. Ламинарное и турбулентное течения, число Рейнольдса. Движение тела в жидкостях и газах. Сила лобового сопротивления и подъёмная сила. Подъёмная сила крыла самолёта, формула Жуковского.

Рассмотрим течение смачивающей жидкости по горизонтальной трубе круглого сечения радиуса r. Жидкость считаем несжимаемой и вязкой. Предположим, что течение стационарное и происходит цилиндрическими слоями, параллельными стенкам трубы.

Обозначим скорость течения в некоторой точке поперечного сече­ния трубы v, расстояние этой точки от оси трубы у.

Выделим внутри жидкости элементарный цилиндрический объем с осью, совпадающей с осью трубы, и боковой поверхностью, парал­лельной стенкам трубы и проходящей через точку с координатой у. Высоту цилиндра вдоль течения обозначим 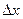(рис. 1). Так как движение стационарное и равномерное, то силы давления, действую­щие на основание цилиндрического объема 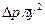, и сила вязкого трения, действующая на боковую поверхность цилиндра

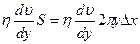должны уравновешиваться.

Cледовательно,

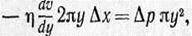
или

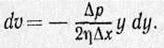
После интегрирования, полагая, что у стенок имеет место прили­пание жидкости, т. е. скорость на расстоянии r от оси равна нулю (v_r=0), получим:

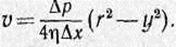(1)

Это соотношение устанавливает закон распределения скоростей течения в данном сечении трубы. Считая падение давления на еди­ницу длины трубы постоянным (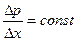) и объединяя постоян­ные, получим:

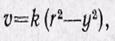(2)

т. е. скорость частиц жидкости распределяется в сечении трубы по параболическому закону. Вершина параболы лежит на оси трубы (рис. 1).

рис.№1 К выводу распределения скорости в цилиндрической трубе.

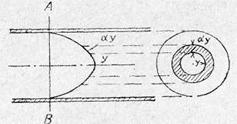рис.№2 К выводу закона Гагена-Пуазейля.  

Непосредственную опытную проверку этого закона про­вести трудно, так как любой измеритель скорости, помещенный в трубу, искажает распределение скоростей в месте измерения. По­этому подсчитаем расход жидкости (количество жидкости, проте­кающей через сечение трубы за единицу времени) в предположении, что выражение (1) справедливо, а затем сравним его с фактиче­ски измеренным расходом. Так как скорость частиц жидкости зави­сит от расстояния от стенки трубы, то мы подсчитаем элементарный расход жидкости через кольцевое сечение радиуса у и толщиной dy (рис. 2), в пределах которой скорость течения можно считать по­стоянной.

За единицу времени через площадь кольцевого сечения вытекает объём жидкости:

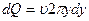(3)

или с учетом равенства (1)

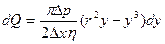(4)

Интегрируя по всем кольцевым сечениям от 0 до r, получим рас­ход жидкости в трубе:

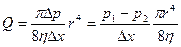. (5)

Разделив расход жидкости на площадь поперечного сечения трубы 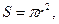получим среднюю скорость в сечении:

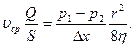(6)

Эта зависимость называется законом Гагена — Пуазейля: средняя скорость параллелоструйного течения жидко­сти в трубе прямо пропорциональна падению напора на единицу длины трубы, квадрату радиуса трубы и об­ратно пропорциональна коэффициенту вязкости жид­кости.

Движение жидкости параллельными слоями называется лами­нарным течением.

Величина 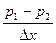равна потере давления на единицу длины трубы,

Так как труба горизонтальна (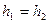) и сечение ее постоянно, то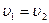. Следовательно,

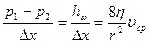, (7)

где 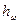—величина диссипации механической энергии единицы объёма жидкости в единицу времени, т. е. сила сопротивления при ламинарном течении прямо пропорциональна первой степени скорости.

Проверка закона Гагена — Пуазейля осуществляется легко. При этом получается неожиданный результат. Уравнение (6) оказывается справедливым лишь при малых скоростях течения жид­кости и.малых размерах труб. Точнее говоря, при малых значениях безразмерного числа

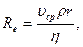
где v_cp— средняя скорость, 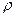— плотность жидкости, r — радиус трубы,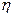— коэффициент вязкости жидкости. Число R_e носит на­звание числа Рейнольдса.

При ламинарном движении жидкость движется слоями, и скорости в каждом сечении параллельны друг другу; скорости частиц жидкости меняются от твердых гра­ниц внутрь потока по параболическому закону; сопро­тивление движению жидкости или твердого тела в ней прямо пропорционально первой степени скорости, причем сопротивление обязано своим происхождением действию сил вязкости.

Если траектории частиц жидкости искривляются, то на них долж­на действовать некоторая сила, сообщающая им центростремитель­ное ускорение. В потоке вязкой жидкости на каждую частицу дейст­вуют сила давления р и сила вязкости F_B. Эти силы и обусловливают возникновение ускорения частиц.

По второму закону Ньютона

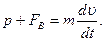
Если система отсчета связана с движущейся частицей, то в этой системе на частицу будет действовать сила инерции, равная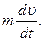

Можно предположить, что степень устойчивости ламинарного течения характеризуется отношением сил инерции к силам вязкости, так как силы инерции, видимо, тем больше, чем больше отклонение траекторий частиц в потоке от прямолинейного направления, а сила вязкости препятствует возникновению этих отклонений.

Силы инерции выражаются через произведение плотности жид­кости на объем и на производную скорости по времени.

Производную от скорости по времени можно представить как величину, пропорциональную отношению:

,

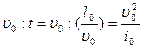где 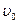—некоторая скорость, характерная для данной задачи, 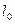—некоторая характерная длина. Масса, т.е. произведение плотности на объём, пропорциональна 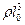. Тогда сила инерции:

=.

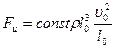Сила вязкости пропорциональна производной скорости по рас­стоянию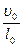некоторой площади 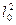и коэффициенту вязкости:

Найдем отношение F_и к F_B. Легко видеть, что оно равно с точ­ностью до постоянного множителя безразмерному числу, которое мы назвали числом Рейнольдса:

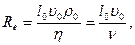(8)

где 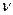—коэффициент кинематической вязкости.

В число Рейнольдса (8) вхо­дят некоторая скоростью, размер /₀ и коэффициент кинематической вяз­кости. Коэффициент вязкости опре­делен, если известна жидкость в потоке, для которого вычисляется значение R_e. Скорость 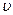₀ есть ско­рость, характерная для данного случая течения жидкости, напри­мер: для течения жидкости в длин­ной трубе это средняя скорость в сечении трубы, для случая обтека­ния жидкостью шарика это ско­рость его движения относительно жидкости и т. д. Характерным раз­мером в случае течения жидкости в трубе служит диаметр трубы, при обтекании малого по сравнению с размерами потока шарика — диаметр шарика и т. д.

Пока число Рейнольдса мало, силы вязкости преоб­ладают над силами инерции и
всякое возмущение, случайно возникшее в жидкости, гаситься.

При возрастании скорости токе воды, и размеров потока (или убы­вании вязкости) силы инерции становятся при прочих равных усло­виях близкими по величине к силам вязкости. Случайные искрив­ления траекторий частиц жидкости возникают легче и существуют дольше. Этому режиму течения жидкости соответствует некоторая область значений числа Рейнольдса, которая называется критической.

Наконец, если число Рейнольдса больше критического значения, силы инерции значительно превышают силы вязкости и случайно возникшие возмущения развиваются в толще потока. На рисун­ке 3 изображено развитие возмущения, возникшего на выступе твердой границы. Со временем весь поток оказывается заполнен­ным возмущениями. Частицы жидкости движутся по искривленным, случайно изменяющимся во времени траекториям. Такое движение называется турбулентным.

Рис.№3 Развитие случайного

возмущения в потоке жидкости.

Переход от ламинарного к турбулентному режиму течения на­блюдается для всех жидкостей при одном и том же значении чис­ла Рейнольдса Re_кр. Следовательно, критическая скорость 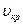, при которой осуществляется этот переход, меняется в зависимости от размеров потока и вязкости таким образом, что критическое значение числа Рейнольдса для всех жидкостей остается постоян­ным.

Ламинарному течению соответствуют значения чисел Рейнольдса примерно до R_e=\000. Переход от ламинарного к турбулентному течению происходит в области значений R_e от 1000 до 2000. При значениях больших 2000 течение турбулентное.

Подъемная сила F_n возни­кает в результате существования циркуляционного движения жид­кости вокруг тела.

Строгая математическая теория подъемной силы разработана великим русским механиком Н. Е. Жуковским. Он показал, что те­чение вблизи крыла можно рассматривать как два одновременно су­ществующих течения идеальной жидкости: непрерывного обтекания с плавно изогнутыми линиями тока и циркуляционного течения во­круг крыла (рис. 4). Частицы жидкости при этом деформируются, но не вращаются, т. е. движение удовлетворяет условию потенциаль­ности. При потенциальном движении особая физическая величина — циркуляция скорости по любому замкнутому геометрическому контуру, охватывающему тело, — величина постоянная.

рис.№4 Возникновение подъёмной силы крыла самолёта.

Найдем подъемную силу. Пусть поток обтекает крыло, располо­женное под углом атаки 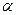к направлению скорости v₀ в невозмущен­ном потоке; давление в невозмущенном потоке р₀. Положим, скоро­сти циркуляционного течения в точках сверху и снизу крыла, от­стоящих на расстоянии х от передней кромки, соответственно 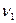и v₂ и давление 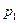и . Напишем уравнение Бернулли для двух тру­бок тока, проходящих одна сверху другая снизу крыла. Одно сече­ние возьмем в невозмущенной части потока, второе — на расстоянии х от передней кромки.

Тогда

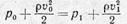
для верхней трубки тока и

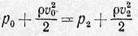
для нижней трубки тока. Отсюда

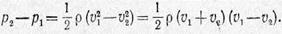
Так как при малых углах атаки v₁ и v₂ мало отличаются от v₀, поло­жим

Тогда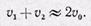

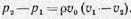
Выделим около точки с координатой х полоску шириной dx вдоль хорды крыла и длиной в направлении размаха крыла /. Результи­рующая сила давления на выделенную полоску:

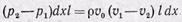
Значение результирующей, действующей на всю поверхность крыла:

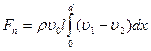
Но интеграл

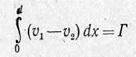
представляет собой циркуляцию скорости по контуру, проведенному вокруг крыла. Таким образом:

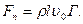
Эта формула носит название формулы Жуковского — Кутта, где

Г=,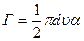

величина циркуляции скорости.

В природе и технике часто происходят процессы, повторяющиеся во времени. Такие процессы называются колебаниями.

Качания маятника часов, волны на воде, переменный электрический ток, свет, звук, и т.д. являются примерами колебаний различных физических величин. Все эти процессы качественно отличаются друг от друга, но оказывается, что количественные закономерности (т. е. математические выражения) этих процессов имеют много общего. Именно это обстоятельство придает учению о колебаниях его важное значение. Изучая на этих двух лекциях механические колебания, мы получим также знания - в других областях, например, из области электромагнитных колебаний, радиотехники, оптики, и др.

Дата добавления: 2014-01-04