Гармонические осцилляторы

Биение

Особый интерес представляет случай, когда два скла­дываемых гармонических колебания одинакового напра­вления мало различаются по частоте. Как мы сейчас пока­жем, результирующее движение при этих условиях можно рассматривать как гармоническое колебание с пульсиру­ющей амплитудой. Такое колебание называется бие­ниями.

Обозначим частоту одного из колебаний буквой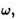частоту второго колебания через 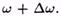По условию Амплитуды обоих колебаний будем полагать одинаковыми и равными а. Чтобы не усложнять без на­добности формул, допустим, что начальные фазы обоих колебаний равны нулю. Тогда уравнения колебаний будут иметь следующий вид:

Складывая эти выражения и применяя тригонометриче­скую формулу для суммы косинусов, получаем

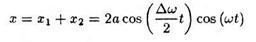
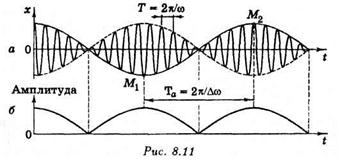
(во втором множителе пренебрегаем членомпо сравнению с и). График функции () изображен на рис. График построен для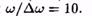

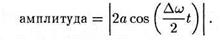
Заключенный в квадратные скобки множитель в фор­муле () изменяется гораздо медленнее, чем второй множитель. Ввиду условия Асо <С и за то время, за кото­рое множитель cos (cjt) совершает несколько полных коле­баний, множитель, стоящий в квадратных скобках, почти не изменяется. Это дает нам основание рассматривать ко­лебание () как гармоническое колебание частоты, амплитуда которого изменяется по некоторому периодиче­скому закону. Выражением этого закона не может быть множитель, стоящий в квадратных скобках, так как он изменяется в пределах от —2а до +2а, в то время как амплитуда по определению — положительная величина.

График амплитуды показан на рис. Аналитическое выражение амплитуды, очевидно, имеет вид

Функция () — периодическая функция с частотой, в два раза превышающей частоту выражения, стоящего под знаком модуля

т. е. с частотой Дол.Таким обра­зом, частота пульсаций амп­литуды — ее называют час­тотой биений — равна разности частот складывае­мых колебаний.

Отметим, что множитель 2а cos (Auj/2t) не только определяет амплитуду, но и влияет на фазу колебания. Это проявляется, например, в том, что отклонения, соответ­ствующие соседним максиму­мам амплитуды, имеют противоположные знаки (см. точ­ки Mi и М2 на рис..

Дата добавления: 2014-01-04