
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Систематические погрешности
|
|
|
|
Классы точности средств измерений
Классификация погрешностей средств измерений
Погрешность средства измерений 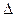 - разность между показанием средства измерений и истинным (действительным) значением измеряемой физической величины.
- разность между показанием средства измерений и истинным (действительным) значением измеряемой физической величины.
Погрешность меры -разность между номинальным значением меры и действительным значением воспроизводимой ею величины. Поскольку истинное значение физической величины неизвестно, то на практике пользуются ее действительным значением, которое воспроизводится образцовым средством измерений или мерой. Для самой меры показанием является ее номинальное значение.
На рисунке 3.1 показана классификация погрешностей средств измерений, в которой они условно разбиты на пять групп в зависимости от природы их происхождения.
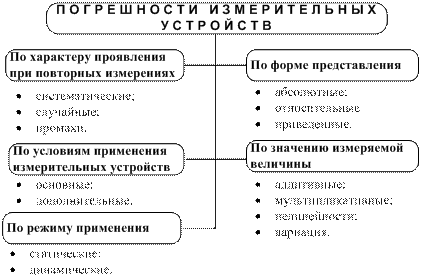
Рисунок 3.1 – Классификация погрешностей средств измерений
Систематическая погрешность средства измерений 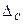 – составляющая погрешности измерения, которая при повторении равноточных измерений остаётся постоянной или закономерно изменяется. Эту погрешность можно исключить или вносить соответствующие поправки.
– составляющая погрешности измерения, которая при повторении равноточных измерений остаётся постоянной или закономерно изменяется. Эту погрешность можно исключить или вносить соответствующие поправки.
Систематическая погрешность конкретного средства измерений, как правило, будет отличаться от систематической погрешности другого экземпляра средства измерений этого же типа, вследствие чего для группы однотипных средств измерений систематическая погрешность может иногда рассматриваться как случайная погрешность. Причины возникновения систематических погрешностей и их классификация будут рассмотрены отдельно.
Случайная погрешность средства измерений  (случайная погрешность) – составляющая погрешности измерения, которая изменяется случайным образом. случайная погрешность может быть обнаружена при повторных измерениях одной и той же величины, когда получаются неодинаковые результаты. Её нельзя исключить, но их влияние на результата измерения может быть теоретически учтено методами теории вероятности и математической статистики.
(случайная погрешность) – составляющая погрешности измерения, которая изменяется случайным образом. случайная погрешность может быть обнаружена при повторных измерениях одной и той же величины, когда получаются неодинаковые результаты. Её нельзя исключить, но их влияние на результата измерения может быть теоретически учтено методами теории вероятности и математической статистики.
Промах -погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда. Иногда вместо термина «промах» применяют термин грубая погрешность измерений.
Промахи связаны с резким нарушением условий испытаний при отдельном наблюдении: толчки, неисправности измерительной аппаратуры, неправильные действия наблюдателя. Результаты измерений, содержащие промахи, должны быть отброшены как недостоверные.
Основная погрешность средства измерений (основная погрешность) - погрешность средства измерений, применяемого в нормальных условиях.
Дополнительная погрешность средства измерений (дополнительная погрешность) - составляющая погрешности средства измерений, возникающая дополнительно к основной погрешности вследствие отклонения какой-либо из влияющих величин от нормального ее значения или вследствие ее выхода за пределы нормальной области значений.
Статическая погрешность средства измерений (статическая погрешность) - погрешность средства измерений, применяемого при измерении физической величины, принимаемой за неизменную.
Динамическая погрешность средства измерений (динамическая погрешность) - погрешность средства измерений, возникающая при измерении изменяющейся (в процессе измерений) физической величины.
Абсолютная погрешность средства измерений (абсолютная погрешность) - погрешность средства измерений, выраженная в единицах измеряемой физической величины
D = хизм – хд , (3.1)
где хизм - измеренное значение, хд – действительное значение измеряемой величины.
Абсолютное значение погрешности -значение погрешности без учета ее знака (модуль погрешности). Необходимо различать термины абсолютная погрешность и абсолютное значение погрешности.
Относительная погрешность средства измерений (относительная погрешность) - погрешность средства измерений, выраженная отношением абсолютной погрешности средства измерений к результату измерений или к действительному значению измеренной физической величины
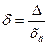 (3.2)
(3.2)
или
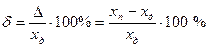 . (3.2*)
. (3.2*)
Приведенная погрешность средства измерения (приведенная погрешность) - относительная погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, по-
стоянному во всем диапазоне измерений или в части диапазона
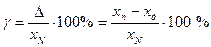 , (3.3)
, (3.3)
где 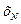 - нормирующее значение. Часто за нормирующее значение принимают верхний предел измерений.
- нормирующее значение. Часто за нормирующее значение принимают верхний предел измерений.
Аддитивная погрешность (по лат. – получаемая путем сложения) – погрешность, не зависящая от измеряемой величины. По закономерности проявления аддитивные погрешности могут быть случайными или систематическими.
Случайная аддитивная погрешность, например, вызываемая трением в опорах измерительного механизма, контактными сопротивлениями, дрейфом нуля и др., при изменении измеряемой величины принимать произвольное, но не зависящее от измеряемой величины значения. Её предельные значения образуют на характеристике полосу постоянной величины (рисунок 3.2,а). Точно такая же картина будет, если погрешность представляется как приведенная, поскольку знаменатель в выражении (3.3) не изменяется на протяжении всей шкалы независимо от значения измеряемой величины.
Примером систематической аддитивной погрешности является смещение нуля характеристики аналогового средства измерения (рисунок 3.2,б).
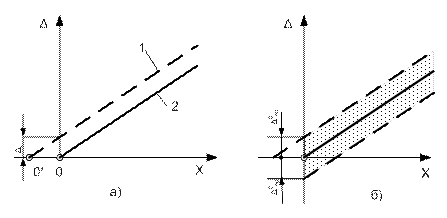
1 - фактическая характеристика, смещенная влево на длину О-О¢ ; 2 – номинальная характеристика прибора; Dс – значение систематической погрешности;
D0пр – предельное значение случайной погрешности
Рисунок 3.2 – Смещение характеристик аналогового измерительного прибора под влиянием аддитивных систематической (а) и случайной (б) погрешностей
Мультипликативная погрешность (по лат. - получаемая путем умножения) – погрешность, величина которой изменяется прямо пропорционально измеряемой величине.
Пример -Источники мультипликативной погрешности – действие влияющих величин на параметры элементов и узлов СИ, например, изменение собственного сопротивления амперметра и встроенного в него шунта при изменении температуры окружающей среды.
В этом случае результат измерения определяется по формуле:
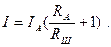
Поскольку при изменении температуры окружающей среды сопротивления 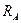 и
и 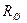 изменяются неодинаково, т.к. сделаны из разных материалов, погрешность измерения будет изменяться пропорционально соотношению этих сопротивлений.
изменяются неодинаково, т.к. сделаны из разных материалов, погрешность измерения будет изменяться пропорционально соотношению этих сопротивлений.
Погрешность нелинейности имеет нелинейную зависимость от измеряемой величины. Чаще всего возникает как систематическая погрешность, связанная с линеаризацией номинальной статической характеристики.
Вариация имеет нелинейную зависимость от измеряемой величины, появляется вследствие гистерезисных явлений, вариации, проявляющейся при подходе к измеряемой точке со стороны меньших и больших значений; проявляется как систематическая погрешность (рисунок 3.3).
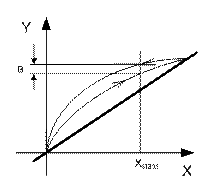
Рисунок 3.3 - Графическое представление вариации
Учёт всех нормируемых метрологических характеристик средств измерений является сложной и трудоёмкой процедурой. На практике такая точность не нужна. Поэтому для средств измерений, используемых в повседневной практике, принято деление на классы точности.
Класс точности средств измерений (класс точности) - обобщенная характеристика данного типа средств измерений, как правило, отражающая уровень их точности, выражаемая нормируемыми метрологическими характеристиками.
Класс точности дает возможность судить о том, в каких пределах находится погрешность средства измерений одного типа, но не является непосредственным показателем точности измерений, выполняемых с помощью каждого из этих средств. Это важно при выборе средств измерений в зависимости от заданной точности измерений. Класс точности средств измерений конкретного типа устанавливают в стандартах технических требований (условий) или в других нормативных документах.
Нормируемые метрологические характеристики типа средства измерений (нормируемые метрологические характеристики) - совокупность метрологических характеристик данного типа средств измерений, устанавливаемая нормативными документами на средства измерений
Требования к нормируемым метрологическим характеристикам устанавливаются в стандартах на средства измерений конкретного типа. Например, для электроизмерительных приборов нормируют:
- пределы допускаемых погрешностей и соответствующие рабочие области влияющих величин;
- пределы допускаемых дополнительных погрешностей и соответствующие рабочие области влияющих величин;
- пределы допускаемой вариации показаний;
- невозвращение указателей к нулевой отметке.
Предел допускаемой погрешности средства измерений (предел допускаемой погрешности, предел погрешности) - наибольшее значение погрешности средств измерений, устанавливаемое нормативным документом для данного типа средств измерений, при котором оно еще признается годным к применению.
При превышении установленного предела погрешности средство измерений признается негодным для применения (в данном классе точности).
Обычно устанавливают пределы допускаемой погрешности, то есть границы зоны, за которую не должна выходить погрешность.
Пример - Для 100-миллиметровой концевой меры длины 1-го класса точности пределы допускаемой погрешности ±50 мкм.
Пределы допускаемой абсолютной основной погрешности устанавливают по формуле
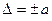 (3.4)
(3.4)
или
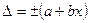 , (3.4*)
, (3.4*)
где 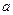 и
и 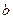 - положительные числа, не зависящие от
- положительные числа, не зависящие от 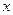 .
.
Пределы допускаемой приведенной погрешности
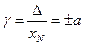 , (3.5)
, (3.5)
где 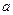 - положительное число, выбираемое из ряда
- положительное число, выбираемое из ряда
(1; 1,5; 2,0; 2,5; 4,0; 5,0; 6,0)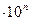 , при
, при 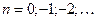 . (3.6)
. (3.6)
Пределы допускаемой относительной основной погрешности определяют из уравнения
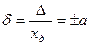 , (3.7)
, (3.7)
если 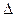 установлено по формуле(3.4).
установлено по формуле(3.4).
Если же D определено по формуле (3.4*), т.е. имеется мультипликативная составляющая погрешности, пределы допускаемой относительной основной погрешности определяют по формуле
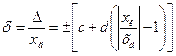 , (3.8)
, (3.8)
где 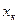 - больший по модулю из пределов измерений;
- больший по модулю из пределов измерений; 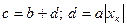 . Значения чисел
. Значения чисел 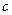 и
и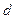 должны быть округлены до чисел из ряда (3.6).
должны быть округлены до чисел из ряда (3.6).
Класс точности средств измерений характеризует их свойства в отношении точности, но не является непосредственным показателем точности измерений, выполняемых с помощью этих средств. Классы точности присваиваются средствам измерений с учётом результатов государственных приёмочных испытаний.
Общие положения о делении средств измерений на классы точности и способы нормирования метрологических характеристик регламентированы ГОСТ 8.401—80. Однако этот стандарт не устанавливает классы точности средств измерения, для которых предусмотрены нормы отдельно для систематической и случайной составляющих погрешности, а также если необходимо учитывать динамические характеристики.
Если класс точности прибора установлен по пределу допускаемой относительной основной погрешности, т.е по значению погрешности чувствительности [см. формулу (3.7)] и форма полосы погрешности принята чисто мультипликативной, обозначаемое на шкале значение класса точности обводится кружком.
Пример - 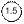 обозначает, что
обозначает, что 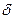 = 1,5 %.
= 1,5 %.
Если же полоса погрешности принята аддитивной и прибор нормируется по пределу допускаемой приведенной основной погрешности [см. формулу (3.5)], т.е. по значению погрешности нуля (таких приборов большинство), то класс точности указывается на шкале без каких-либо подчеркиваний.
Пример - 1,5 обозначает, что 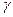 =1,5 %.
=1,5 %.
Если шкала прибора неравномерная (например, у омметров), предел допускаемой основной приведенной погрешности выражается формулой (3.5), а нормирующее значение принято равным длине шкалы или ее части, класс точности обозначается на шкале одним числом, помещенным между двумя линиями, расположенными под углом.
Пример - 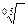 обозначает, что
обозначает, что 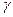 =0,5 %.
=0,5 %.
Если средство измерений обладает как аддитивной, так и мультипликативной полосой погрешности, а пределы допускаемой относительной погрешности в процентах устанавливаются формулой (3.8), классы точности обозначают числами с и d (в процентах), разделяя их косой чертой.
Пример – Если установлено, что для средства измерения 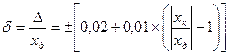 , где с = 0,02; d = 0,01, то обозначение в документации будет «класс точности 0,02/0,01», а на приборе 0,02/0,01.
, где с = 0,02; d = 0,01, то обозначение в документации будет «класс точности 0,02/0,01», а на приборе 0,02/0,01.
Для средств измерений, пределы допускаемой основной погрешности которых принято выражать в форме абсолютных погрешностей по формуле (3.4), классы точности обозначают прописными буквами латинского алфавита или римскими цифрами. Чем дальше буква от начала алфавита, тем больше погрешность. Расшифровка соответствия букв значению абсолютной погрешности осуществляется в технической документации на средство измерения.
Для всех рассмотренных случаев вместе с условным обозначением класса точности на шкале, щитке или корпусе средств измерений наносится номер стандарта или технических условий, устанавливающих технические требования на эти средства измерений. Таким образом, обозначение класса точности средства измерений дает достаточно полную информацию для вычисления приближенной оценки погрешностей результатов измерений.
Примеры обозначения классов точности на шкалах приборов приведены на рисунке 3.4.
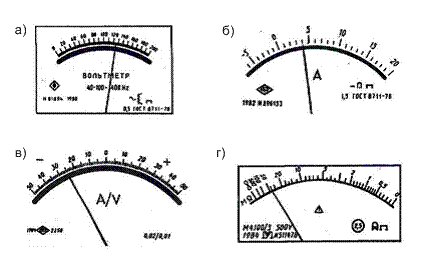
а – вольтметр класса точности 0,5 с равномерной шкалой;
б – амперметр класса точности 1,5 с равномерной шкалой; в – амперметр класса точности 0,02/0,01 с равномерной шкалой; г - мегаомметр класса
точности 2,5 с неравномерной шкалой.
Рисунок 3.4 - Лицевые панели приборов
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 568; Нарушение авторских прав?; Мы поможем в написании вашей работы!