Погрешности косвенных измерений

При косвенных измерениях измеряемая величина 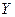, функционально связана с одной или несколькими непосредственно измеряемыми величинами .

Рассмотрим простейший случай определения ошибки одной переменной, когда 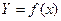. Имеем

.

Разложив правую часть этого равенства в ряд Тейлора и пренебрегая членами разложения, содержащими 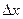в степени выше первой, получим выражение абсолютной погрешности

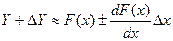или . (3.40)

Относительная ошибка измерения функции определится из выражения

. (3.41)

Если измеряемая величина Y является функцией нескольких переменных Y= f(), то абсолютная погрешность результата косвенных измерений будет равна

, (3.42)

где , , 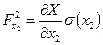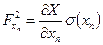- частные производные от Y по ; и т.д. – средние квадратические отклонения результатов прямых измерений величин .

Относительная погрешность результата косвенных измерений равна

. (3.43)

Пример - Пусть параметр 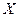функционально связан с измеряемыми параметрами зависимостью

.

Применив формулу (3.42), имеем

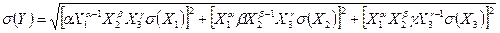
или в относительной форме

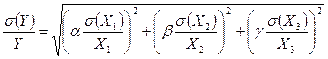. (3.44)

В большинстве практических случаев мы имеем дело с косвенными измерениями, в которых участвуют только два прямых измерения. Согласно теории вероятностей среднее квадратическое значение отклонения суммы двух величин от её математического ожидания вычисляется по формуле

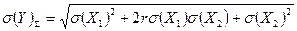, (3.45)

где - коэффициент корреляции.

По степени коррелированности погрешности обычно подразделяют на два вида:

- cильнокоррелированные ,

- cлабокоррелированные .

Тогда из (3.44) для сильнокорелированных величин имеем

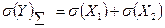, (3.46)

для слабокоррелированных

. (3.47)

Погрешность измерительной системы, состоящей из 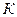последовательно соединённых приборов (или преобразователей), необходимо рассматривать как ряд независимых случайных погрешностей и вычислять на основании вышеприведённой формулы для слабокоррелированных (независимых) погрешностей.

Формулы для вычисления абсолютных и относительных погрешностей измерения некоторых, наиболее часто встречающихся в измерительной технике, функций приведены в таблице 3.4.

Таблица 3.4 – Формулы для вычисления погрешностей косвенных измерений

Функциональная связь	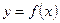Соотношение между среднеквадратическими ошибками

Пример - Пусть .

Значение абсолютной погрешности равно 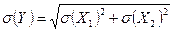или в относительной форме .

Дата добавления: 2014-01-04