Проверка нормальности результатов наблюдений

Проверку гипотезы о том, что результаты наблюдений принадлежат нормальному распределению, следует проводить с уровнем значимости q от 10 до 2 %. Конкретные значения уровней значимости должны быть указаны в конкретной методике выполнения измерений.

При числе результатов наблюдений n < 50 нормальность их распределения проверяют при помощи составного критерия.

Критерий 1. Вычисляют отношение

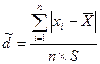, (4.1)

где S - смещенная оценка среднего квадратического отклонения, вычисляемая по формуле (3.27)

Результаты наблюдений группы можно считать распределенными нормально, если

,

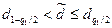где 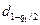и - квантили распределения, получаемые из таблицы 4.1 по n, q ₁/2 и (1 – q ₁/2), причем q ₁ - заранее выбранный уровень значимости критерия.

Таблица 4.1 - Статистика d

n	q 1/2 ´ 100%	(1- q 1/2) ´ 100%
1 %	5 %	95 %	99 %
	0,9137	0,8884	0,7236	0,6829
	0,9001	0,8768	0,7304	0,6950
	0,8901	0,8686	0,7360	0,7040
	0,8826	0,8625	0,7404	0,7110
	0,8769	0,8578	0,7440	0,7167
	0,8722	0,8540	0,7470	0,7216
	0,8682	0,8508	0,7496	0,7256
	0,8648	0,8481	0,7518	0,7291

Критерий 2. Можно считать, что результаты наблюдений принадлежат нормальному распределению, если не более m разностей превзошли значение z_p/2 S_n, где S_n - оценка среднего квадратического отклонения, вычисляемая по формуле (3.28); z_p/2 - верхний квантиль распределения нормированной функции Лапласа, отвечающий вероятности Р/2.

Значения Р определяются из таблицы 4.2 по выбранному уровню значимости q₂ и числу результатов наблюдений n.

Таблица 4.2 - Значения Р для вычисления

n	m	q2 ´ 100 %
1 %	2 %	5 %
		0,98	0,98	0,96
11-14		0,99	0,98	0,97
15-20		0,99	0,99	0,98
21-22		0,98	0,97	0,96
		0,98	0,98	0,96
24-27		0,98	0,98	0,97
28-32		0,99	0,98	0,97
33-35		0,99	0,98	0,98
36-49		0,99	0,99	0,98

При уровне значимости, отличном от предусмотренных в таблицы 4.2, значение Р находят путем линейной интерполяции.

В случае, если при проверке нормальности распределения результатов наблюдений группы для критерия 1 выбран уровень значимости q ₁, а для критерия 2 - q ₂, то результирующий уровень значимости составного критерия q ≤ q ₁ + q ₂.

В случае, если хотя бы один из критериев не соблюдается, то считают, что распределение результатов наблюдений группы не соответствует нормальному.

Дата добавления: 2014-01-04