Правила округления результатов измерения

Точность обработки числового материала должна быть согласована с точ­ностью самих измерений. Вычисления, проведённые с большим числом деся­тичных знаков, требуют лишних затрат труда и создают ложное впечатление о большей точности измерений. В то же время, разумеется, не следует ухудшать результаты измерений, пользуясь излишне грубыми методами вычислений.

Как правило, при обработке результатов измерений в промежуточных расчетах удерживают на одну значащую цифру больше, чем в первичных данных. Значащими цифрами являются все цифры в десятичном представлении числа, кроме нулей, стоящих в начале числа. Нули в середине числа или в конце числа (справа) - значащие цифры. Например, в числе 0,3070 первый нуль не являются значащим, а третий и пятый - знача­щие.

В случае больших целых чисел с нулями на конце их следует записывать в так называемом стандартном виде

A = A₀ × 10 ⁿ,

где число n - порядок числа A, а основание числа A₀ находится в промежутке [1;9].

Пример - Число 47000 следует записы­вать в виде 4,7 × 10⁴, если оно имеет две значащие цифры, или 4,70 × 10⁴, если оно имеет три значащие цифры и т.д.

При округлении лишних или недостоверных чисел придерживаются следующих правил:

- последняя сохраняемая цифра не изменяется, если:

а) первая отбрасываемая цифра, считая слева направо, меньше 5;

б) первая отбрасываемая цифра, равная 5, получилась в результате преды­дущего округления в большую сторону;

- последняя сохраняемая цифра увеличивается на единицу, если:

а) первая отбрасываемая цифра больше 5;

б) первая отбрасываемая цифра, считая слева направо, равна 5 при отсутст­вии предыдущих округлений или при наличии предыдущего округления в меньшую сторону.

Округление следует выполнять сразу до желаемого количества значащих цифр, а не по этапам, что может привести к ошибкам.

При выполнении различных математических операций с приближёнными числами руководствуются следующими правилами:

- при сложении и вычитании в результате сохраняют столько десятичных знаков, сколько их содержится в числе с наименьшим количеством деся­тичных знаков;

- при умножении и делении в результате сохраняют столько значащих цифр, сколько их содержится в числе с наименьшим количеством знача­щих цифр;

- результат расчёта значений функций хⁿ, 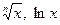некоторого прибли­жённого числа Х должен содержать столько значащих цифр, сколько их имеется в числе Х.

Если некоторые приближённые числа содержат больше десятичных знаков (при сложении и вычитании) или больше значащих цифр (при умножении, де­лении, возведении в степень и т.д.), чем другие, то их предварительно округля­ют, сохраняя только одну лишнюю цифру.

При вычислении погрешности, если первоначально полученное число начинается с цифры 1 или 2, то отбрасывание второго знака приводит к очень большой ошибке (до 30 – 50 % от полученного при этом округлении результата), что не­допустимо. Исходя из этого, на практике установилось следующее правило округления:

- если полу­ченное число начинается с цифры, равной или большей, чем 3, то в нём сохраняется лишь одна значащая цифра;

- если же оно начинается с цифры, меньшей 3, то есть с цифры 1 или 2, то в нём сохраняется две значащие цифры.

В соответствии с этим правилом установлены и нормируемые значения погреш­ностей средств измерений: в числах 1,5 и 2,5 указываются две значащие цифры, но в числах 0,5; 4; 6 указывается один знак.

На практике применяются следующие три правила округления рассчитанного значения погрешности и полученного результата измерения:

Дата добавления: 2014-01-04