Сети и потоки на сетях. Постановка задачи о максимальном потоке

Матричное задание графа. Упорядочение вершин.

При большом числе вершин и дуг/ребер изображение графа теряет наглядность. В этих случаях для задания графов и работы с ними используют матрицы.

1. Граф без петель, имеющий n вершин и m дуг/ребер можно задать матрицей инциденций, строки которой соответствуют вершинам, а столбцы – дугам. Элементы матрицы, размерности n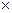m, определяются по формуле

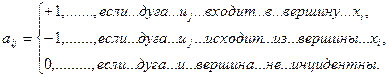
Для неориентированного графа вместо ”-1” ставится 1.

Пример.

2. Граф можно матрицей смежности вершин, строки и столбцы которой соответствуют вершинам графа. Элементы матрицы S_ij равны числу дуг/ребер, идущих из х_i в х_j. Матрица смежности для неориентированного графа будет симметричной.

Пример.

Аналогично может быть задана матрица смежности дуг/ребер.

Расчеты в задачах, связанных с графами, заметно упрощаются, если их элементы упорядочены.

Если существует путь из х_i в х_j, то вершина х_i называется предшествующей вершине х_j, а х_j – последующей х_i.

Упорядочение вершин связного графа без контуров означает разбиение его вершин на группы так, чтобы:

1) вершины 1-й группы не имели предшествующих, а вершины последней – последующих;

2) вершины любой другой группы не имели предшествующих в следующей группе;

3) вершины одной и той же группы не соединялись с дугами.

Графический способ упорядочения вершин (алгоритм Фалкерсона).

1. Находятся вершины графа, в которые не входит ни одна дуга. Такие вершины образуют

1-ю группу.

2. Вершины и выходящие из них дуги установленной группы исключаются из дальней-

шего рассмотрения.

3. Устанавливается следующая группа вершин, в которые не входит ни одна дуга.

4. Если процесс упорядочения не окончен, то переход п. 2.

5. В полученном графе, изоморфном исходному, перенумеровываются вершины.

Пример.

Сеть – конечный взвешенный связный орграф без контуров и петель, ориентированный в одном общем направлении от вершины I (исток, вход) к вершине S (сток, выход).

Для наглядности представим, что по ребрам от истока к стоку направляется некоторое вещество (груз, ресурс, информация и т.п.).

Максимальное количество r_ij вещества, которое может пропустить за единицу времени ребро (i, j), называется его пропускной способностью. В общем случае r_ij ≠ r_ji. Если вершины не соединены, r_ij = 0. Т.к. нет петель, то r_ii = 0. Пропускную способность можно задать квадратной матрицей.

Количество х_ij вещества, проходящего по ребру (i, j) в единицу времени, называется потоком по ребру (i, j). Предполагается, что если из х_i в х_j направляется поток х_ij, то из x_j в x_i направляется поток (-х_ij)

x_ij = - x_ji. (1)

Поток по каждому ребру не превышает его пропускную способность

x_ij r_ij (i = ; j = ). (2)

Количество вещества, притекающее в вершину, равно количеству вещества, вытекающего из неё

(i I, S). (3)

Совокупность Х = потоков по всем рёбрам сети называют потоком по сети. Общее количество вещества вытекающего из истока I, совпадает с общим количеством вещества, поступающего в сток S, т.е.

F = x_Ij = x_iS. (4)

Функцию F называют мощностью потока.

Если на сети задан поток Х = , то ребро (i,j) называется насыщенным, если поток x_ij по нему совпадает с его пропускной способностью r_ij (x_ij = r_ij), и ненасыщенным, если x_ij < rij.

Задачу о максимальном потоке можно сформулировать следующим образом: найти совокупность Х* = {x*_ij} потоков x*_ij по всем рёбрам сети, которая удовлетворяет условиям (1) – (3) и максимизирует линейную функцию (4). Это типичная ЗЛП.

Замечание. Не всякие n² чисел могут задавать поток по сети. Только такие n² чисел x_ij задают поток, которые удовлетворяют условиям (1) – (3).

Пример.

Дата добавления: 2014-01-04