Радиоимпульса. Сечения АКФ и их анализ

Время-частотная функция рассогласования одиночного

Введение

На предыдущей лекции мы рассмотрели основные свойства время-частотной функции рассогласования когерентных сигналов и сделали вывод о том, что анализ этой функции, основных ее сечений, позволяет решать вопросы оценки разрешающей способности сигналов и осуществлять выбор сигнала, удовлетворяющего требованиям к указанной характеристике. Кроме того, параметры и вид АКФ влияют и на другие характеристики РЛС, например, на точность измерения координат целей, однозначность измерений. В этой связи рассмотрим время-частотные функции конкретных сигналов, в частности радиоимпульсов без внутриимпульсной модуляции и их когерентных последовательностей, построим сечения АКФ этих сигналов и определим области эффективного их применения для решения задачи разрешения сигналов.

Цель лекции - дать систематизированные основы научных знаний об АКФ когерентных сигналов без внутриимпульсной модуляции и применении результатов анализа их сечений в интересах оценки разрешающей способности РЛС.

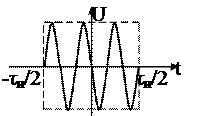Пусть дан прямоугольный радиоимпульс с немодулированной несущей, комплексная амплитуда которого вещественна и равна

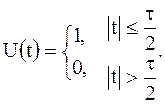(1)

Подставим (1) в формулу для нормированной время-частотной функции рассогласования, получим

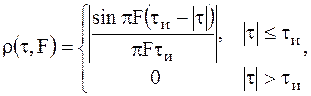(2)

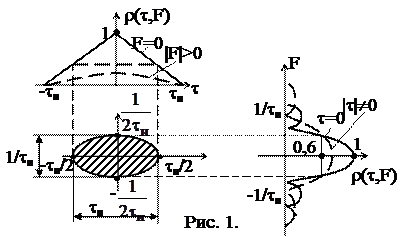Сечения тела неопределенности плоскостями 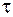, F=const и ρ=1/2 выглядят следующим образом:

Сечение плоскостью F=0 описывается выражением

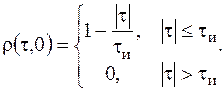(3)

Поскольку рассматриваемый радиосигнал является узкополосным, т.е.

n=П ^. τ_и=1,

то мера разрешающей способности по времени запаздывания и дальности равна

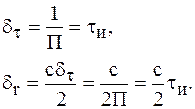(4)

Она зависит от ширины спектра сигнала. Зависимость ρ от τ для различных F=const можно рассматривать как кривые огибающих напряжений на выходе оптимального фильтра при расстройке F по несущей частоте. Расстройка ведет к уменьшению пикового значения и к искажению формы огибающей (рис.1).

Сечение АКФ плоскостью τ=0

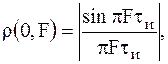(5)

представляет собой энергетический спектр огибающей прямоугольного радиоимпульса.

Его протяженность на уроне 0,5 оценивается величиной

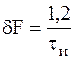
и является мерой разрешающей способности по доплеровской частоте.

Соответственно разрешающая способность по скорости будет равна

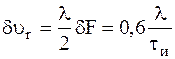
и зависит от длительности сигнала.

На рис.1 также показаны зависимости ρ от F для различных τ=const.

Каждая из этих кривых соответствует спектру прямоугольного видеоимпульса длительностью 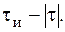Функция ρ(0,F) позволяет также определить количество частотных каналов, необходимых для обработки импульса данной длительности в диапазоне доплеровских частот.

Она находится из условия перекрытия участка площади «время запаздывания-частота» минимальным числом сечений АКФ на некотором уровне ρ(τ,F)= ρ_доп.

Характерной особенностью этого сигнала является невозможность получения высоких разрешающих способностей одновременно по времени запаздывания и частоте. Сужение АКФ по оси τ (за счет сокращения длительности сигнала τ_и) приводит к его расширению по оси F (и наоборот) (см. рис.2).

В случае разрешения сигналов резко различной интенсивности существенным для разрешения становится малый уровень боковых лепестков тела неопределенности. Лучшую разрешающую способность в этом смысле обеспечивает колокольный радиоимпульс с огибающей

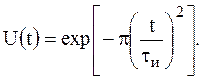
За счет скругления огибающей сигнала тело рассогласования этого радиоимпульса не имеет боковых лепестков:

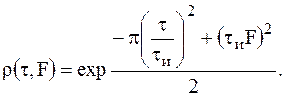
Таким образом, применение одиночных узкополосных радиоимпульсов принципиально не позволяет получить высокие разрешающие способности одновременно по времени запаздывания и доплеровской частоте. При разрешении сигналов важное значение также имеет уровень боковых лепестков тела неопределенности.

Дата добавления: 2014-01-04