Двоичные сумматоры

Одноразрядным двоичным сумматором (ОДС) называется КЦУ, которое предназначено для сложения двух одноразрядных двоичных чисел с учетом переноса из соседнего младшего разряда. УГО ОДС показано на рисунке 22.

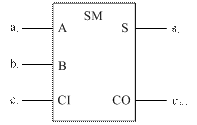
Рисунок 22 – Условное графическое обозначение ОДС

ОДС имеет три входа для подачи разрядов слагаемых a_i, b_i и переноса из соседнего младшего разряда c_i. На выходах ОДС формируется сумма s_i и перенос в соседний старший разряд c_i+1. Принцип работы ОДС поясняется следующей таблицей истинности (таблица 6).

Таблица 6 – Таблица истинности ОДС

Логические аргументы	Логические функции
ai	bi	ci	si	ci+1

Минимизируем логические функции s_i и c_i+1 табличным методом с помощью карт Карно. Для этого по данным таблицы 6 заполним карты Карно (рисунок 23).

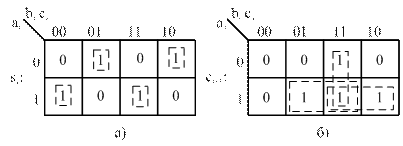
Рисунок 23 – Минимизация функций ОДС. Карты Карно для выхода суммы s_i (а) и выхода переноса c_i+1 (б)

Выполним необходимые объединения и запишем результат минимизации в МДНФ:

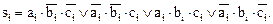….(15)

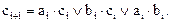….(16)

Очевидно, что функция s_i не поддается минимизации, так как на рисунке 23 а все конституенты единицы изолированы. Логическая схема ОДС, построенная по функциям (15) и (16), показана на рисунке 24.

Многоразрядные двоичные сумматоры (МДС) в зависимости от способа ввода кодов слагаемых делятся на два типа: последовательного действия и параллельного действия. В МДС последовательного действия коды чисел вводятся в последовательной форме, т.е. разряд за разрядом, начиная с младшего. В МДС параллельного действия каждое слагаемое подается в параллельной форме, т.е. одновременно всеми разрядами.

Логическая схема МДС последовательного действия (рисунок 25) состоит из одноразрядного двоичного сумматора (ОДС), выход СО (от англ. Carry Output) которого соединен со входом СI (от англ. Carry Input) через D-триггер. Сдвиговые регистры 1 и 2 служат для подачи на входы сумматора разрядов слагаемых, а регистр 3 – для приема результата суммирования.

Операция суммирования во всех разрядах слагаемых осуществляется с помощью одного и того же ОДС.

С первым тактовым импульсом (ТИ) на входы ОДС поступают из регистров 1 и 2 цифры первого разряда слагаемых a₀ и b₀, а из D-триггера на вход СI подается нулевой сигнал. Суммируя поданные на входы цифры, ОДС формирует первый разряд суммы s₀, выдаваемый на вход регистра 3, и перенос c₁, принимаемый в D-триггер. Второй ТИ осуществляет в регистрах сдвиг на один разряд вправо, при этом на входы ОДС подаются цифры второго разряда слагаемых a₁, b₁ и c₁. Получающаяся цифра второго разряда суммы s₁ вдвигается в регистр 3, перенос c₂ принимается в D-триггер и т.д.

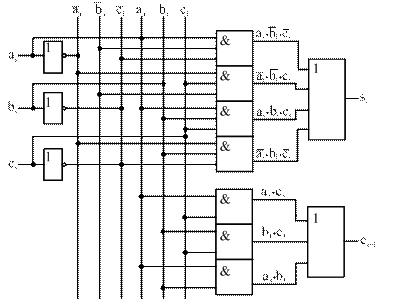
Рисунок 24 – Логическая схема ОДС

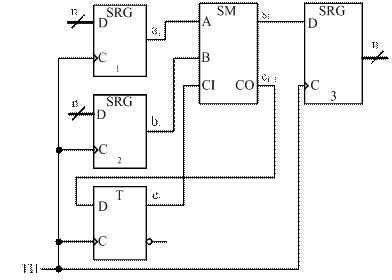
Рисунок 25 – Логическая схема МДС последовательного действия

Достоинством МДС последовательного действия является малый объем оборудования, требуемый для его построения, а недостатком – низкое быстродействие, так как время суммирования T_SM пропорционально разрядности слагаемых.

МДС параллельного действия в зависимости от способа передачи переносов от младших разрядов в старшие могут быть двух типов:

– с последовательным переносом;

– с параллельным (ускоренным) переносом.

Логическая схема МДС параллельного действия с последовательным переносом (рисунок 26) состоит из отдельных разрядов, каждый из которых содержит ОДС.

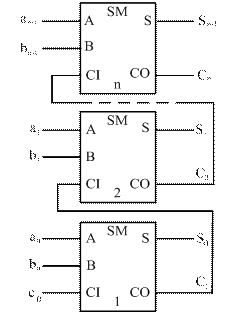
Рисунок 26 – Логическая схема МДС параллельного действия с последовательным переносом

При подаче слагаемых цифры их разрядов поступают на соответствующие ОДС. Каждый из ОДС формирует на своих выходах цифру соответствующего разряда суммы и перенос в соседний старший разряд. Сигнал переноса в каждом разряде формируется после того, как будет сформирован и передан сигнал переноса из предыдущего разряда. В худшем случае, возникший в младшем разряде перенос может последовательно вызывать переносы во всех остальных разрядах. При этом время передачи переносов T_C = n t_{C ОДС}, где t_{C ОДС} – задержка распространения в одном разряде. Таким образом, последовательный перенос в МДС параллельного действия не обеспечивает высокое быстродействие.

Для обеспечения высокого быстродействия в МДС параллельного действия сигналы переносов формируются одновременно для всех разрядов с помощью блока ускоренного переноса. На рисунке 27 показана функциональная схема четырехразрядной секции МДС параллельного действия с параллельным переносом.

При этом разрядные сумматоры не содержат цепей формирования переносов, они формируют только сумму s_i и функции G_i, P_i, для получения которых переносы не требуются. Эти вспомогательные функции генерации переноса и распространения переноса необходимы для формирования переносов в блоке ускоренного переноса GRP (рисунок 27). Исходя из этого, выражение (16) можно представить в следующем виде:

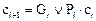. (17)

Из выражения (17) следует, что сигнал переноса на выходе i-го разряда генерируется самим разрядом (G_i = 1) при 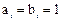независимо от результата переноса из соседнего младшего разряда. Следовательно, можно передавать сигнал переноса для обработки старших разрядов, не дожидаясь окончания формирования переносов из младших разрядов. Однако, если только один из сигналов a_i, b_i равен единице, то перенос в следующий разряд будет иметь место только при наличии переноса из предыдущего разряда (P_i = 1, c_i = 1). Таким образом, сигналы переноса в каждом разряде формируются одновременно в соответствии с выражением (17).

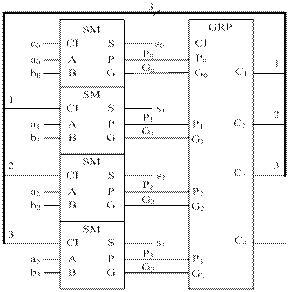
Рисунок 27 – Функциональная схема четырехразрядной секции сумматора с ускоренным (параллельным) переносом

Дата добавления: 2014-01-04