
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры решения задач. Пример 1. Протон влетает в однородное магнитное поле с индукцией 20 мкТл перпендикулярно линиям индукции магнитного поля
|
|
|
|
Пример 1. Протон влетает в однородное магнитное поле с индукцией 20 мкТл перпендикулярно линиям индукции магнитного поля. Сколько оборотов в секунду будет делать протон в магнитном поле?
Решение
На заряженную частицу в магнитном поле действует сила
 , (а)
, (а)
где 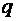 – заряд частицы,
– заряд частицы, 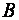 – индукция магнитного поля,
– индукция магнитного поля, 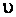 – скорость частицы,
– скорость частицы, 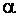 – угол между векторами
– угол между векторами 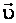 и
и 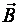 .
.
В данной задаче 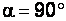 , значит протон будет двигаться в магнитном поле по окружности радиуса
, значит протон будет двигаться в магнитном поле по окружности радиуса 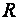 с центростремительным (нормальным) ускорением
с центростремительным (нормальным) ускорением
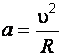 (б)
(б)
По второму закону Ньютона
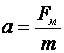 , (в)
, (в)
где 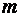 – масса частицы.
– масса частицы.
Приравнивая правые части выражений (б) и (в), с учетом формулы (а), получаем
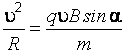 , (г)
, (г)
так как 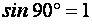 , то после небольшого преобразования получаем
, то после небольшого преобразования получаем
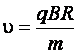 . (д)
. (д)
С другой стороны,
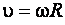 , (е)
, (е)
где  – угловая скорость.
– угловая скорость.
Получаем
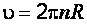 . (ж)
. (ж)
Приравняем правые части уравнений (д) и (л), получим
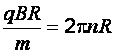 ,
,
откуда выразим 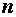 – частоту вращения, т. е. число оборотов в секунду,
– частоту вращения, т. е. число оборотов в секунду,
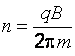 . (и)
. (и)
Размерность: 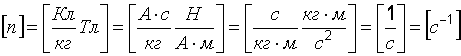 .
.
Подставляем числовые значения в формулу (и):
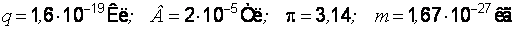 .
.
Вычисления дают 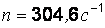 .
.
Пример 2. Электрон, имеющий скорость 8·106 м/с, влетает в однородное магнитное поле с индукцией 31,4 мТл под углом 30° к его направлению. Определите радиус и шаг винтовой линии, по которой будет двигаться электрон (рис. 24).
Решение
Скорость  разложим на две составляющие: тангенциальную
разложим на две составляющие: тангенциальную 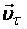 , параллельную линиям индукции магнитного поля и нормальную
, параллельную линиям индукции магнитного поля и нормальную 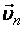 , перпендикулярную им,
, перпендикулярную им,
 ; (а)
; (а)
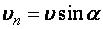 . (б)
. (б)
На электрон действует магнитная сила (благодаря нормальной составляющей скорости)
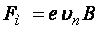 . (в)
. (в)
Под действием этой силы электрон будет двигаться по окружности радиуса 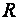 , который можно найти из условия:
, который можно найти из условия:
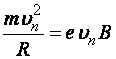 , (г)
, (г)
так как сила Лоренца является центростремительной силой.
Из формулы (г) получаем
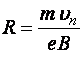 , (д)
, (д)
где 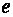 – модуль заряда электрона;
– модуль заряда электрона; 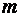 – масса электрона;
– масса электрона; 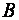 – индукция магнитного поля.
– индукция магнитного поля.
Вдоль силовых линий поля магнитная сила не действует, поэтому частица движется прямолинейно с постоянной скоростью 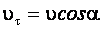 .
.
В результате суперпозиции двух движений электрон будет двигаться по винтовой линии радиусом  и шагом винта
и шагом винта  :
:
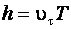 , (е)
, (е)
где 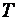 – период движения по окружности,
– период движения по окружности,
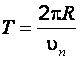 . (ж)
. (ж)
С учетом формул (б), (д) и (ж), уравнение (е) принимает вид:
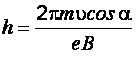 . (и)
. (и)
Размерность: 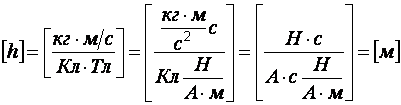 .
.
Подставляем числовые данные в выражение (и):
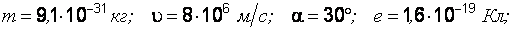
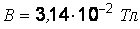 .
.
Вычисления дают:
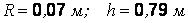 .
.
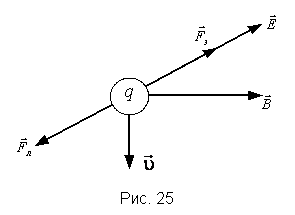
Пример 3. Перпендикулярно магнитному полю с индукцией 0,1 Тл возбуждено электрическое поле напряженностью 1·105 В/м. Перпендикулярно обоим полям, не отклоняясь от прямолинейной траектории, движется заряженная частица. Найти скорость этой частицы (рис. 25).
Решение
Согласно условию задачи, частица движется равномерно и прямолинейно (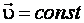 ). По первому закону Ньютона геометрическая сумма сил, действующих на частицу, равна нулю. В данном случае на частицу действует сила Лоренца ). По первому закону Ньютона геометрическая сумма сил, действующих на частицу, равна нулю. В данном случае на частицу действует сила Лоренца
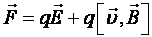 ,
где ,
где  – электрическая составляющая силы Лоренца, – электрическая составляющая силы Лоренца, 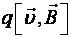 – её магнитная составляющая (рис. 25). – её магнитная составляющая (рис. 25).
| 
|
Следовательно, 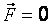 , т. е. электрическая и магнитная силы равны по модулю и противоположно направлены:
, т. е. электрическая и магнитная силы равны по модулю и противоположно направлены:
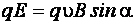
откуда скорость частицы равна:
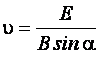
Согласно условию 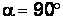 (
(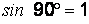 ), поэтому
), поэтому
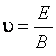 .
.
Размерность:
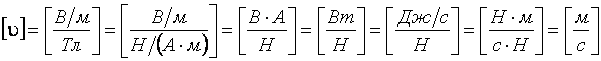 .
.
Подставляем числовые данные: 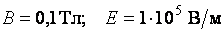 .
.
Получаем при вычислении: 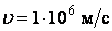 .
.
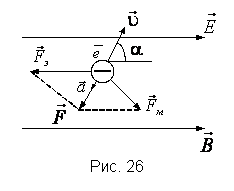
Пример 4. Электрон влетает со скоростью 600 м/с в область пространства, где имеются сонаправленные однородные электрическое и магнитное поля, под углом 60° к силовым линиям полей. Напряженность электрического поля 0,2 кВ/м, индукция магнитного поля 20 мТл. С каким ускорением станет двигаться электрон в этой области пространства? (рис. 26).
Решение
Согласно второму закону Ньютона, ускорение электрона имеет вид:
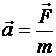 ,
где ,
где 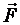 – сила Лоренца, действующая на электрон со стороны электрического и магнитного полей; – сила Лоренца, действующая на электрон со стороны электрического и магнитного полей; 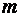 – масса электрона.
Сила Лоренца определяется по формуле – масса электрона.
Сила Лоренца определяется по формуле
| 
|
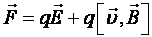 ,
,
где 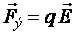 – электрическая составляющая силы Лоренца;
– электрическая составляющая силы Лоренца; 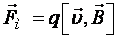 – её магнитная составляющая (рис. 26).
– её магнитная составляющая (рис. 26).
Вектор 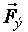 направлен противоположно вектору
направлен противоположно вектору 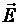 , так как заряд электрона отрицательный. Вектор магнитной силы
, так как заряд электрона отрицательный. Вектор магнитной силы 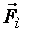 перпендикулярен вектору магнитной индукции. Следовательно, векторы
перпендикулярен вектору магнитной индукции. Следовательно, векторы 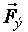 и
и 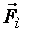 взаимно-перпендикулярны.
взаимно-перпендикулярны.
Модуль силы находится по теореме Пифагора:
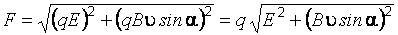 ,
,
где  – модуль заряда электрона (элементарный заряд).
– модуль заряда электрона (элементарный заряд).
Ускорение
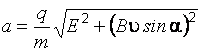 .
.
Направление  совпадает с направлением вектора
совпадает с направлением вектора  , определяемом по правилу сложения векторов.
, определяемом по правилу сложения векторов.
Подставим числовые значения:
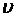 = 600 м/с;
= 600 м/с; 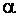 = 60°;
= 60°; 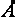 = 0,2 кВ/м = 200 В/м;
= 0,2 кВ/м = 200 В/м; 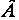 = 20 мТл = 2·10-2 Тл;
= 20 мТл = 2·10-2 Тл;  = 1,6 ·10-19 Кл;
= 1,6 ·10-19 Кл; 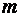 = 9,11·10-31 кг.
= 9,11·10-31 кг.
Вычисления дают:  = 3,5 ·1013 м/с2.
= 3,5 ·1013 м/с2.
Пример 5. Шарик массой 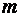 , заряженный положительным зарядом
, заряженный положительным зарядом 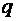 и подвешенный на нити длиной
и подвешенный на нити длиной 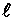 , движется по окружности в вертикальном однородном магнитном поле с индукцией. Определите кинетическую энергию шарика, если во время движения нить образует угол
, движется по окружности в вертикальном однородном магнитном поле с индукцией. Определите кинетическую энергию шарика, если во время движения нить образует угол 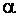 с вертикалью.
с вертикалью.
Решение
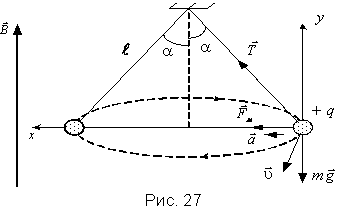
Выберем систему отсчета x0y, начало которой поместим в ту точку пространства, где находится шарик в начальный момент времени. Предположим, что нить – невесома, нерастяжима и неэлектропроводна. Заряженный шарик примем за материальную точку. Заряд шарика будем считать точечным.
На шарик действуют сила тяжести 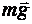 , сила натяжения нити
, сила натяжения нити 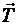 и сила
и сила 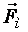 со стороны магнитного поля (рис. 27).
со стороны магнитного поля (рис. 27).
|
По второму закону Ньютона
 . (а)
. (а)
Направление всех сил указано на рис. 27 в предположении, что вектор магнитной индукции направлен вверх, а шарик движется по часовой стрелке.
Запишем уравнение (а) в проекциях на выбранные оси координат
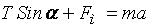 ; (б)
; (б)
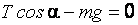 . (в)
. (в)
После преобразования, получаем
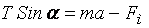 ; (г)
; (г)
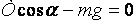 . (д)
. (д)
Разделим (г) на (д), получим
 . (и)
. (и)
Шарик движется с нормальным ускорением 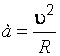 , (к)
, (к)
где 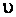 – линейная скорость шарика по окружности,
– линейная скорость шарика по окружности, 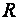 – радиус окружности.
– радиус окружности.
Из чертежа следует:
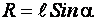 . (л)
. (л)
Сила Лоренца определяется выражением
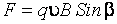 , (м)
, (м)
где 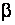 = 90° (по условию задачи),
= 90° (по условию задачи),
С учетом выражений (к)–(м) уравнение (и) принимает вид:
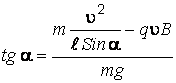 ,
,
или
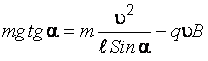 .
.
Решаем квадратное уравнение относительно переменной 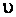 :
:
 ,
,
получаем
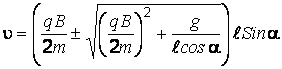 .
.
Так как модуль скорости 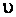 > 0, то из последнего выражения следует:
> 0, то из последнего выражения следует:
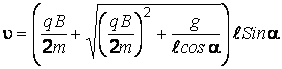 .
.
Кинетическая энергия определяется соотношением:
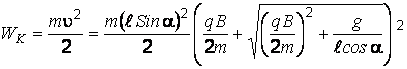 .
.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 11255; Нарушение авторских прав?; Мы поможем в написании вашей работы!