Нагрев аппаратов при коротком замыкании

При расчете температуры элементов аппаратов в режиме короткого замыкания благодаря малой длительности этого режима можно пренебречь теплом, отдаваемым во внешнюю среду, и считать, что все тепло расходуется на повышение температуры проводника. В этом случае энергетический баланс проводника, имеющего сопротивление R и массу М, выражается уравнением

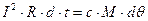
Ввиду того, что температура может достигать больших значений (300°С), необходимо учитывать изменение как сопротивления R, так и удельной теплоёмкости С от температуры. Изменение сопротивления проводника от температуры

,

где:

- коэффициент добавочных потерь;

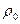- удельная теплоемкость при О°С;

α - температурный коэффициент сопротивления материала;

q - сечение проводника;

l - длина проводника.

Зависимость удельной теплоемкости от температуры

,

где:

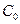- удельная теплоемкость при О°С;

β - температурный коэффициент теплоемкости.

Выразив

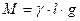
и подставив в эти выражения после упрощения имеем

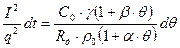
В результате интегрирования получим

где:

δ - плотность тока;

и - значения интеграла правой части при верхнем(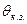) и нижнем (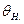) пределах интегрирования.

С целью упрощения расчетов построены кривые 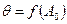для различных материалов. С помощью этих кривых легко произвести расчет на термическую стойкость аппарата. В соответствии со свойствами проводника и изоляции выбирается допустимая температура при коротком замыкании 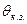, и при номинальном токе . С помощью кривых находим и, соответствующие температурам 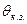и. Зная 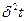можно при данных t и I определить сечение проводника q, либо при известных t и q найти допустимый ток короткого замыкания. Если известен допустимый ток при времени , то допустимый ток при времени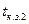

Уравнение не учитывает теплоотдачу в окружающую среду, поэтому им можно пользоваться при времени не более 10 c.

Если используется материал, для которого нет кривых, аналогичных, то при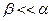расчёт термической устойчивости производят по формуле

При коротком замыкании вблизи генератора из-за переходных процессов величина переменной составляющей тока, протекающего через аппарат, меняется. В этом случае расчет термической стойкости ведется по установившемуся току короткого замыкания_∞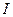

Время прохождения установившегося тока 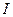_∞ принимается равным фиктивному времени

Фиктивное время - это время, при котором тепло, выделяющееся при прохождении установившегося тока 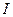_∞ равно теплу, выделяющемуся при прохождении реального тока за реальное время протекания.

Фиктивное время для периодической составляющей тока короткого замыкания 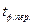находится с помощью кривых. Для данного генератора определяют ( 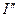- действующее значение сверхпереходного тока) и зная действительное время прохождения тока 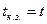и β, находят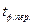

Фиктивное время для апериодической составляющей тока может быть определено

Фиктивное время

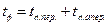
Дата добавления: 2014-01-04