Составляем уравнения движения для многомассовой механической части

Допущения:

1. Силы и моменты, действующие в системе, приложены к сосредоточенным массам, которые не подвергаются деформации.
2. Упругие связи невесомы.
3. Деформация упругих звеньев линейна и подчиняется закону Гука.
4. Волновым движением деформации пренебрегаем.

Наиболее удобный метод составления уравнений движения механизмов – метод уравнений Лагранжа II рода. При этом предполагается, что движение механизма исследуется в системе обобщённых координат, в качестве которых должны быть приняты независимые параметры, определяющие положение механизма, а именно углы поворота вращающихся вокруг неподвижных осей дискретных инерционных элементов или их линейные перемещения.

Уравнение Лагранжа II рода в общем виде:

где:

– кинетическая энергия системы (движущееся тело)

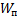– потенциальная энергия (скручивание, растяжение)

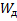– работа сил рассеяния (диссипативная функция Релея)

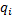– обобщённая координата

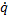– обобщённая скорость

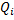– обобщённая внешняя сила, соответствующая обобщённой координате.

– сумма элементарных работ 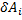всех действующих сил на возможном перемещении

Обобщённый параметр	Вращательное движение	Поступательное движение

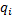
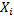
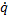
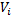
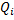
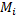
Расчётные схемы 3-х и 2-х массовых систем.

Число уравнений Лагранжа II рода для системы равно числу дискретных инерционных элементов, т.е. числу степеней свободы механизма.

Для механической системы, содержащей n инерционных и (n-1), упругих элементов:

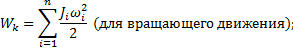
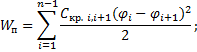
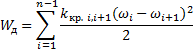
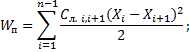
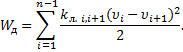
Моменты (силы), входящие в левую часть уравнения Лагранжа II рода и действующие на i-й инерционный элемент системы определяются как

Инерционные:

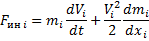
Потенциальные:

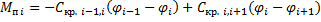
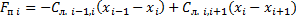
Диссипативные:

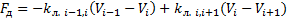
В соответствии с уравнением Лагранжа 2 рода для любого i -го элемента (звена) может быть записано уравнение движения:

.

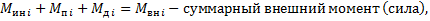
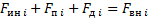
Если момент инерции звена J (масса m) не зависят от его положения, то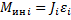

Диссипативными силами можно пренебречь ввиду их малости.

Уравнения для 3-х массовой системы имеют вид:

Для 2-х массовой системы:

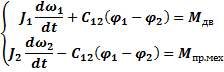
Дата добавления: 2014-01-04