Інтегрування дробово-раціональних функцій

СПИСОК РЕКОМЕНДОВАНИХ ДЖЕРЕЛ

Основна література

1. ДБН В.2.2-9-99. Громадські будинки і споруди. Основні положення. К.: Держбуд України, 2004. - 46 с.

2. ДБНВ.2.2-20:2008. Громадські будинки і споруди. Готелі. К.:Мінрегіонбуд України, 2009. – 39 с.

3. ДБНВ.2.2-25:2009. Громадські будинки і споруди. Підприємства харчування (заклади ресторанного господарства). К.:Мінрегіонбуд України, 2010. – 85 с.

4. Кравченко В.С., Саблій Л.А., Давидчук В.І., Кравченко Н.В Інженерне обладнання будівель..- К.: Видавничий дім Професіонал, 2008. – 480 с.

5. Ливчак Й.Ф., Иванова Н.В. Основы санитарной техники. -М.: Высш.шк., 1984. – 184 с.

6. Соснин Ю.П. Инженерные сети, оборудование зданий и сооружений. - М. Высшая школа, 2005. – 416 с.

Додаткова література

1. Байлик С.И. Гостиничное хозяйство. Проблемы, перспективы, сертификация. – Киев: ВИРА-Р, 2001. – 208 с.

2. ГОСТ 28681.4-95. Міждержавннй стандарт. «Туристсько-екскурсійне обслуговування».- Мінськ / МСМС СНД, 1997.

3. Костенко Е.М. Системы кондиционирования и вентиляции. – К.: Основа. 2006. – 448 с.

4. Ляпина И.Ю. Организация и технология гостиничного обслуживания. – М.: ПрофОбрИздат, 2001. – 207 с.

5. Роглєв Х.Й. Основи готельного менеджменту. Навч посібник. – К.: Кондор, 2005. - 256 с.

6. СНиП 2.04.01-85. Внутренний водопровод и канализиция зданий. – М.: Госком СССР по делам строительства, 1986. – 56 с.

7. СНиП 2.01.02-85. Протипожежні норми. – М.: Госком СССР по делам строительства, 1986. – 8 с.

8. СНиП 2.04.05-91. Отопление, вентиляция и кондиционирование. – М.: Госком СССР по делам строительства, 1992. – 64 с.

9. Шаповал С.Л. Громадс ьке будівництво. Курс лекцій. – К.: КНТЕУ, 2008. – 208 с.350

Означення. Раціональним дробом називається дріб вигляду , де Р(х) та Q (х) - многочлени. Раціональний дріб називається правильним, коли степінь Р(х) нижчий степеня Q (х), в протилежному випадку дріб називається неправильним. У неправильному дробі завжди можна виділити цілу частину і зобразити його у вигляді суми многочлена та правильного раціонального дробу. Кожний правильний дріб розкладається на суму елементарних раціональних дробів типу:

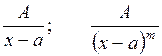(m – ціле число, m > 1),

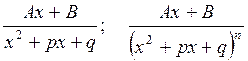(n – ціле число, n > 1, квадратний тричлен х² + рх +q не має дійсних коренів).

Такий розклад є єдиний, але методи розкладу різноманітні, з яких найбільш уживаний метод невизначених коефіцієнтів. Цей метод ґрунтується на наступному:

1) якщо задано неправильний раціональний дріб, треба виділити з нього цілу частину, тобто привести до вигляду:

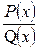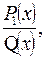= де М(х) – многочлен, а - правильний раціональний дріб;

2) розкласти знаменник дробу на прості множники першого та другого степеня:

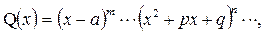де 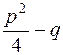< 0, тобто тричлен 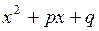не має дійсних коренів;

3) правильний раціональний дріб розкласти на суму елементарних:

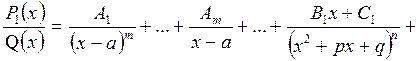
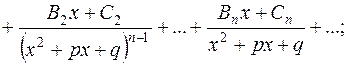
обчислити невизначені коефіцієнти А₁, А₂,…, А_m,…, В₁, С₁, В₂, С₂,…, В_n, С_n,…; для цього привести останню рівність до спільного знаменника, а потім порівняти коефіцієнти при однакових степенях х в лівій і правій частинах одержаної тотожності та розв’язати систему лінійних рівнянь відносно невідомих коефіцієнтів. Ці невідомі коефіцієнти можна знайти іншим способом, надаючи в одержаній тотожності змінній х довільних числових значень. В багатьох випадках корисно використовувати обидва способи обчислення невідомих коефіцієнтів.

4) Розглянемо інтегрування елементарних раціональних дробів:

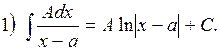
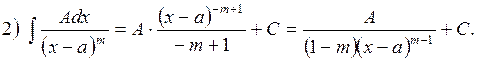
<0.

Спочатку виділяють в чисельнику дробу похідну знаменника, тобто чисельник записують в вигляді:

Тоді:

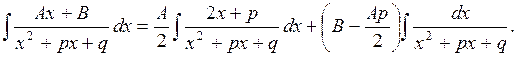
В першому інтегралі чисельник є похідною знаменника, тому

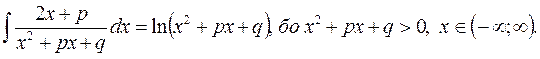
Перш ніж знайти другий інтеграл, треба перетворити квадратний тричлен в знаменнику, виділивши повний квадрат:

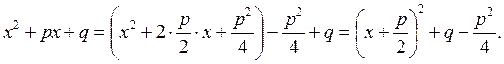
Тоді другий інтеграл зводиться до табличного арктангенса, або “високого” логарифма.

Приклад 1. Знайти інтеграл: .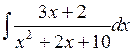

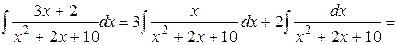
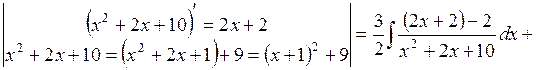
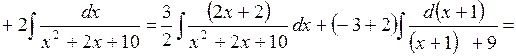
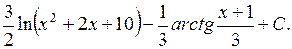
Зауваження. Якщо квадратний тричлен має вигляд (ax²+bx+c), тоді його треба перетворити так:

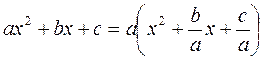і звести знаходження інтеграла 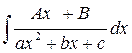до розглянутого раніше інтеграла .

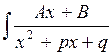Приклад 2. Знайти інтеграл .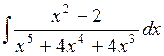

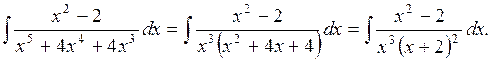
Розкладемо дріб на елементарні дроби.

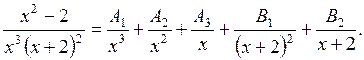
Зведемо до спільного знаменника вираз у правій частині та прирівняємо чисельники дробів.

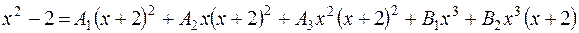
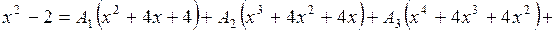
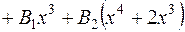
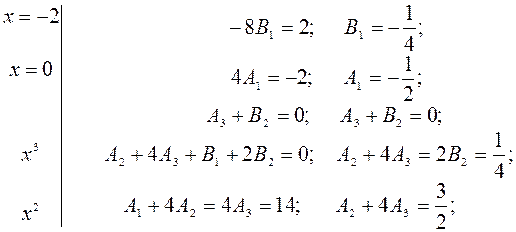
Звідки ,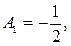

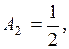
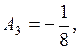
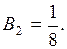
Остаточно отримаємо

.

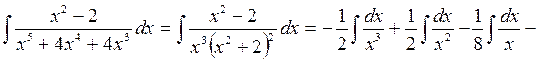
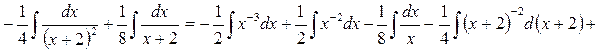
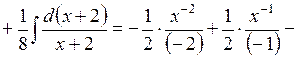
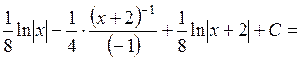
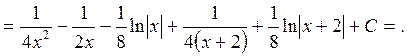
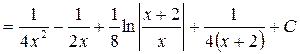Зауваження. Інтеграл виду 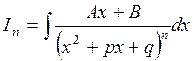, 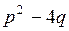< 0, n ³ 2 підстановкою 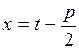зводиться до суми інтегралів:

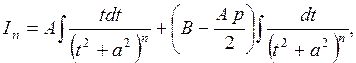
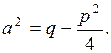
Перший з цих інтегралів обчислюється безпосередньо, а другий за рекурентною формулою:

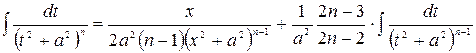
Інтегрування найпростіших ірраціональних функцій.

а) Інтеграли типу 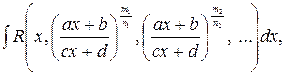де R - раціональна функція, m₁, n₁, m₂, n₂, …- цілі числа, зводяться до інтегралів від раціональних функцій підстановкою 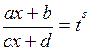де s – спільний знаменник показників степенів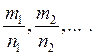

Приклад 3. Знайти інтеграл: .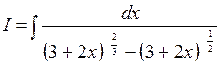

Спільний знаменник дробів , дорівнює s = 6. Застосовуємо підстановку 3+2х = t⁶ звідки 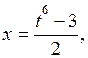тоді ,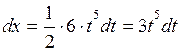

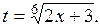
Отже,

.

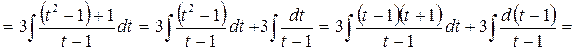
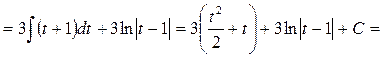
Інтегрування деяких тригонометричних функцій.

Інтеграли типу 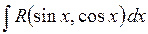зводяться до інтегралів від раціональних функцій за допомогою універсальної підстановки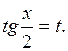

Тоді

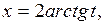
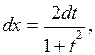
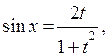
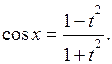
Приклад 4. Знайти інтеграл: .

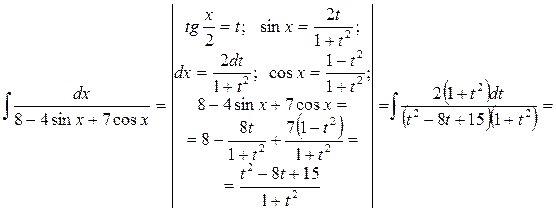
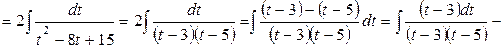
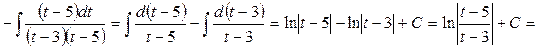
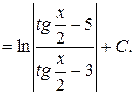
Слід зауважити, що універсальна підстановка в багатьох випадках веде до складних обчислень, тому на практиці здебільшого застосовують інші підстановки, за допомогою яких швидше можна знайти інтеграл, а саме:

а) якщо 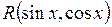- непарна функція відносно 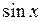, тобто якщо 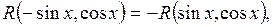то приймають cos x = t;

б) якщо 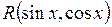- непарна функція відносно 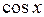, тобто якщо 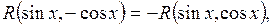то приймають sin x = t;

в) якщо 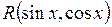- парна функція відносно 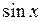і 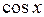, тобто якщо 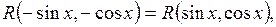то приймають tg x = t.

Приклад 5. Знайти інтеграл: .

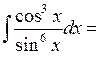
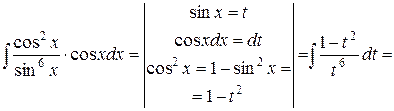
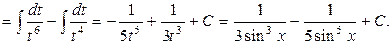
Приклад 16. Знайти інтеграл: .

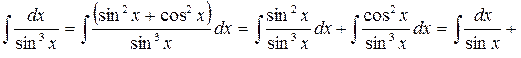
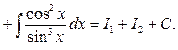
Розглянемо кожен інтеграл окремо:

.

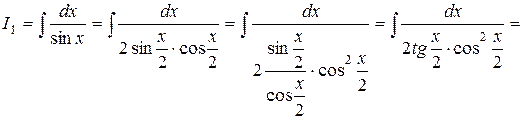
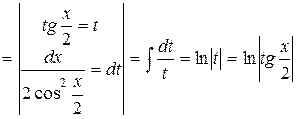Для знаходження І₂ скористаємося методом інтегрування частинами.

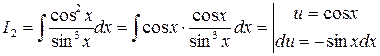
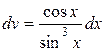
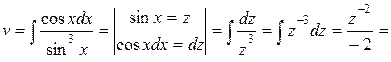
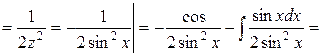
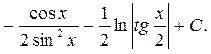
Остаточно матимемо:

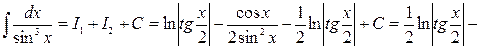
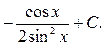
Дата добавления: 2014-01-04