В 5. Аналитическая концепция индексов

В аналитической концепции индексного анализа реализуется современная цель экономического исследования, проводимого с помощью индексов (см. вопрос1). При проведении исследования очень важно установить не только общее изменение результативного показателя, но и какая доля или часть изменения приходится на влияние динамики факторов, входящих в модель.

Аналитическая концепция индексов позволяет установить:

1.) динамику каждого индивидуального показателя,

2.) в какой мере общее изменение результативного показателя зависит от изменения каждого фактора, его составляющего.

Чтобы грамотно использовать аналитическую концепцию индексов, необходимо факторы в модели располагать в следующей последовательности:

– модель (формула) должна быть составлена в строгом соответствии с фактическими связями технико-экономических факторов;

– на первое место в построенной модели выносятся количественные (объемные) показатели, такие как объем произведенной продукции, количество животных или площадь пашни и т.д.;

– на втором месте указывается структурный показатель, например, доля каждого вида продукции в общем объеме реализации;

– на третьем месте в модели стоят качественные (интенсивные) показатели, такие как цена или себестоимость продукции;

Рассмотрим использование аналитической концепции индекса на примере общепринятое разложение индекса товарооборота:

Анализ требует установить, как изменится объём товарооборота под влиянием:

1) динамики количества товаров;

2) динамики цен;

3) изменения структуры различных видов товаров.

Простейшее разложение этого индекса будет иметь вид

I_qp=I_q*I_p (8.11)

или в развернутом виде:

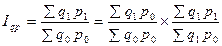(8.12)

Индекс объёма Индекс Индекс цены

товарооборота количества товаров

и структуры

Рассмотрим составляющие этой формулы. Исходным в анализе является индекс товарооборота или выручки.

5.1) 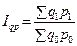(8.13)

– этот индекс отражает общую динамику стоимости товара без анализа факторов, влияющих на это изменение.

5.2) 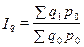(8.14)

– этот индекс называется индексом количества и структуры товара и отражает динамику стоимости товара за счёт динамики объёма реализации;

5.3) 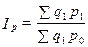(8.15)

– этот индекс носит название индекса цен и анализирует динамику стоимости товара за счёт изменения цен.

Например, если I_qp =1,2658 =126,58%, т.е. общее изменение стоимости товара составило 126,6% или возросло на 26%, то составляющие индекса выручки (или товарооборота) покажут, какая доля влияния приходится на динамику объёма товара, какая – на динамику цены. Так, например, I_q=1,1543 и I_p=1,0966. Значения этих индексов показывают, что выручка (товарооборот) выросла на 15,43% за счет роста объемов реализации продукции и улучшения структуры товара и на 9,66% – за счет роста цен.

Сторонники такого анализа считают, что с помощью индексов решаются три главные задачи:

1) измеряются факторы в общей динамике показателей;

2) обособляется влияние структуры явлений от изменения индексируемого признака при анализе динамики вторичных признаков;

3) измеряются результаты изменения признаков с несоизмеримыми элементами.

Эти три задачи отражают следующее:

1) индекс – есть относительная величина, вследствие чего мы абстрагируемся от абсолютного размера явления;

2) индекс выражает изменение одного показателя во взаимосвязи с другими факторами, от изменений которых мы абстрагируемся, предполагая поочередно их величину неизменной, т.е. в индексе всегда есть элемент условности.

В 6. Агрегатная форма построения индексов. Классификация агрегатных индексов по составу.

Поскольку виды продукции разнородны, и непосредственно их суммировать нельзя, экономистами найдены два основных показателя, позволяющих объединять любые виды продукции в единую систему: это денежное (стоимостное) выражение продукции или выражение её (продукции) в затратах труда, т.е. в виде произведений qp, qz, qt.

Произведения вида qp, qz, qt – называются агрегатами, а индексы, построенные на их основе – агрегатными, т. е. в агрегатном индексе и числитель и знаменатель представлены в виде суммы агрегатов.

По сути Г. Пааше и Э. Ласпейрес заложили основу для построения агрегатных индексов. Поэтому все индексы, входящие в формулу (8.9), являются агрегатными. Рассмотрим подробнее систему показателей, входящих в агрегатный индекс.

Показатели z, p, t, m являются интенсивными или качественными, а показатель q – объёмным или количественным.

В агрегатном индексе могут меняться (индексироваться) или оба показателя, или один из них.

Показатель, который в индексе меняется во времени, называется индексируемым, который не меняется — весами или соизмерителем.

В зависимости от того, сколько показателей изменяется, различают индексы переменного и постоянного состава.

Например, рассмотрим систему агрегатных индексов, отражающих затраты на производство продукции.

6.1) 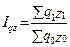— (8.16)

агрегатный индекс, в котором индексируются (изменяются) оба показателя. Следовательно, этот индекс будет индексом переменного состава или с переменными весами. В экономическом исследовании он будет показывать, во сколько раз изменились затраты во времени или по сравнению с эталоном (планом и т.д.).

Данный индекс может быть представлен в виде произведения двух следующих индексов постоянного состава. В соответствии с порядком индексирования факторов, входящих в агрегат (модель), сначала необходимо проиндексировать количественный показатель q, при неизменном значении качественного фактора z.

6.2) Индекс 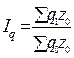(8.17)

– является агрегатным индексом постоянного состава, т.к. здесь индексируемая величина количество продукции q, а z (себестоимость единицы продукции) является соизмерителем, т.к. суммировать можно только денежное выражение несопоставимой продукции. При построении данного индекса используется еще одно правило: соизмеритель (z) берется за базисный период. Данный индекс показывает, во сколько раз изменились затраты на производство продукции за счет изменения объема производства и его структуры.

Затем будем индексировать качественный фактор, входящий в модель (агрегат) – z (себестоимость единицы продукции).

6.3) Индекс 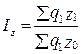(8.18)

– также является агрегатным, постоянного состава. Однако индексируемая величина z здесь качественный показатель (уровень себестоимости единицы продукции), а q (количество продукции) – веса (частота или повторяемость) себестоимости. Поскольку влияние на затраты объема продукции q было отражено в предыдущем индексе (8.17), то его значение берется за отчетный период.

Этот индекс отражает изменение затрат на производство, связанное с изменением себестоимости единицы продукции.

Примечания:

– Поскольку в формулах появляются показатели, где один фактор взят за отчетный период, а второй – за базисный (например, 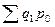), то такое произведение называют условным показателем за условный период.

– Если в экономической модели больше двух показателей, то в индексе переменного состава могут индексироваться (изменяться) все показатели.

– Общий индекс переменного состава разлагается на столько индексов постоянного состава, сколько факторов включено в модель.

– В индексе 8.17 соизмерителем является качественный показатель (z), его принято брать за базисный период; в индексе с 8.18 весами является количественный показатель (q), его берут за отчётный период. При ином распределении “времени” весов и соизмерителя может нарушаться соответствие между индексами и абсолютными показателями, т.е. нарушается равенство и аналитическая концепция индексов.

Итак, в этом вопросе мы выяснили не только понятие агрегатных индексов, но и деление их на индексы по виду весов (по составу) – переменного и постоянного состава в соответствии с классификацией (см. вопрос 3).

В 7. Классификация агрегатных индексов по содержанию.

Рассмотрим деление агрегатных индексов на качественные и количественные на примере индексов объёма товарооборота переменного состава и его разложения на индексы постоянного состава (формула 8.12).

7.1) 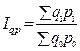(8.19)

Это агрегатный индекс переменного состава. Кроме того, он будет объёмным (или количественным) в силу того, что здесь индексируется (изменяется) обобщающий объёмный показатель – товарооборот (выручка или стоимость товара).

Для индексов постоянного состава этот вопрос решается иначе. Отнесение индекса к количественному или качественному зависит от того, какой фактор (количественный или качественный) индексируется (изменяется).

7.2) 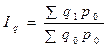(8.20)

– Это агрегатный индекс постоянного состава. Он показывает, во сколько раз изменился товарооборот (выручка) за счет изменения количества и структуры товара. В индексе количества и структуры товара отражена динамика объёмного показателя (q), поэтому этот индекс является объёмным или количественным.

7.3) 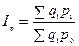(8.21)

– Данный агрегатный индекс цен постоянного состава отражает изменение выручки за счет изменения цен. В индексе цен определяющей является динамика качественного показателя – цены (р) и влияние её на товарооборот, поэтому этот индекс является качественным.

В 8. Классификация агрегатных индексов по базе сравнения.

Если в индексном анализе сравниваются показатели за два периода, то эти индексы носят название базисных. Если система индексов построена на показателях, взятых как минимум за 3 периода и более, причём каждый последующий показатель сравнивается как с начальным уровнем, взятым за базу сравнения, так и с предыдущим, то первые из них индексы являются базисными, а вторые – цепными. Кроме того, при построении системы необходимо учитывать состав индексов, в зависимости от цели исследования и базы сравнения показателей.

В формулах это может выглядеть следующим образом.

Базисные индексы выручки (стоимости товара) переменного состава:

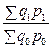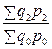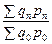;;…; (8.22)

Цепные индексы выручки (стоимости товара) переменного состава:

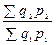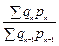; ; …; (8.23)

Можно построить системы цепных и базисных индексов постоянного состава. Например,

базисные индексы физического объема постоянного состава:

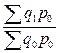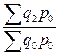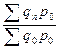; ;...; (8.24)

цепные индексы физического объема постоянного состава:

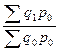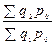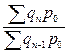; …; (8.25)

Кроме того, между цепными и базисными индексами установлены математические зависимости, которые могут быть использованы в конкретном экономическом анализе. Зная базисные индексы, можно построить цепные и наоборот.

Дата добавления: 2014-01-04