Лекція 5. Проектування комбінаційних схем з використанням мультиплексора

При проектуванні комбінаційних схем треба прагнути, щоб кількість використаних логічних елементів була міні­мальною. Під час реалізації перемикальних функцій в окремих випадках можна зменшити кількість логічних елементів (корпусів мікросхем), використову­ючи мультиплексори та дешифратори [8].

Мультиплексор – це мікросхема, що відноситься до мікросхем середнього ступеня інтеграції і виконує функції комутації в одному напрямі сигналів, що надходять з р можливих напрямів [3].

На рисунку 2.2 для прикладу наведено мультиплексор, який містить вісім інформаційних входів D₀, D₁, …, D₇; три керуючих (адресних) входи А₁, А₂, А₃ і один строб-вхід С.

Будь-який з восьми інформаційних входів може бути зв’язаний з виходом Y, що здійснюється подачею на входи А₁, А₂, А₃ керуючого слова.

Перемикальна функція, що реалізується таким мультиплексором, має вигляд:

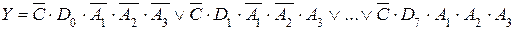(2.10)

Задаючи на інформаційних входах мультиплексора D_i усі константи 0 або 1, можна сформувати той набір конституент одиниці, який відповідає ДДНФ заданої функції, тобто можна реалізувати довільну функцію змінних А ₁, А ₂ …A_n.

Застосування мультиплексора для реалізації перемикальної функції від n змінних грунтується на розкладанні функції за m змінними [7]. Таке розкладання дозволяє виключити m з n змінних перемикальної функції, подавши її через інші функції, що залежать лише від n–m змінних.

Рисунок 2.2 – Умовне графічне позначення мультиплексора з p=8

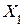Наприклад, розкладання за змінними та 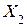має вигляд:

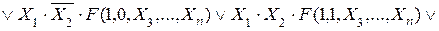
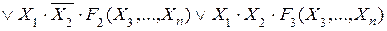, (2.11)

де,,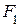,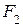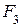— функції від n-2 змінних.

Такому поданню функції відповідає схема (див. рис. 2.3):

де,,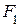,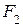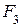— функції від n-2 змінних.

Функції - 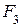можна реалізувати будь-яким способом.

Нехай задано функцію 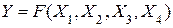від 4 змінних, якій відповідає діаграма Вейча на рис.2.4.

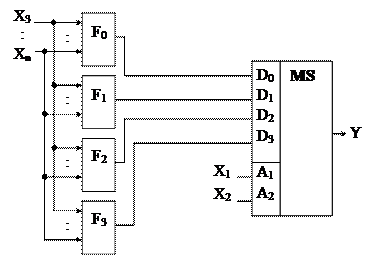Рисунок 2.3 – Реалізація функції від n змінних за допомогою мультиплексора з двома входами управління

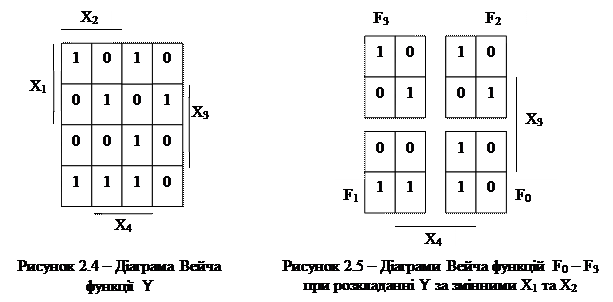
Розкладання функції Y за змінними та 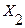має вигляд:

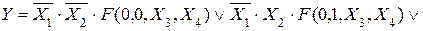
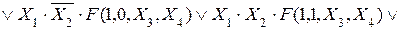
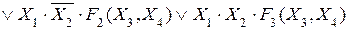2.12)

Розкладання Y за та 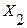дає такі функції - :

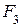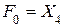, (2.13)

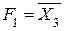, (2.14)

, (2.15)

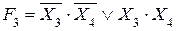. (2.16)

Якщо для реалізації функцій -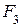необхідно застосувати, наприклад, 2-входові елементи І–НЕ, то 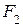та 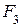слід подати у формі І–НЕ/І–НЕ:

, (2.17)

. (2.18)

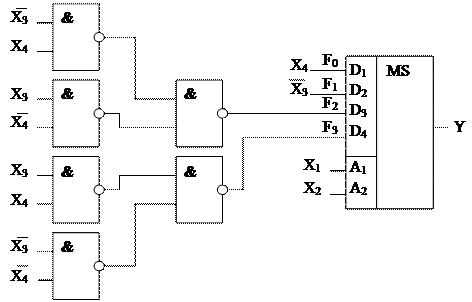Комбінаційна схема, яка реалізує функцію Y за допомогою мультиплексора з двома входами управління, показана на рисунку 2.6.

Рисунок 2.6 – Реалізація функції Y за допомогою мультиплексора

(функції -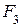відповідають розкладанню Y за змінними 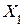та)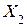

Але функцію Y можна розкласти також за змінними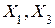; ; ; ; 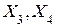. Складність схеми у кожному випадку може бути різною. Тому для отримання найпростішої схеми необхідно порівняти усі КС, кожній з яких відповідає своя пара змінних, за якими виконано розкладання функції Y.

Таким чином, у разі реалізації перемикальної функції з використанням мультиплексора складність схем залежить від того, які змінні виключаються під час розкладання функції. Для отримання найпростішої схеми необхідний перебір усіх комбінацій змінних, що виключаються.

Дата добавления: 2014-01-04