I. Временные характеристики

Математические модели непрерывных САУ в форме дифференциальных уравнений, передаточных функций, детализированных структурных схем СДСС; взаимосвязь моделей

Под математическими моделями САУ понимают формы (способы) их математического описания.

1. Дифференциальные уравнения описывают динамику системы.

Пусть – входы, y(t) – выходная переменная.

Дифференциальное уравнение звена в общей форме:

(1)

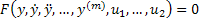
Где – порядок ДУ. Эта форма неудобна для нахождения решения ДУ 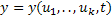, т.к. неподготовлена для интерпретирования.

ДУ, разрешенное относительно старшей производной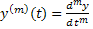

(2)

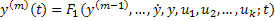
Здесь ДУ подготовлено для интегрирования после которого можно понизить порядок ДУ на единицу.

Уравнения состояния.

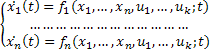
Где 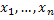– переменные состояния, связь которых с выходной переменной y определяется уравнением выхода (4)

Если система во времени не меняется и воздействия на нее постоянны, т.е. , то говорят, что она находиться в статическом режиме. Уравнения статического режима для ДУ вида (1):

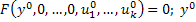– установившееся состояние.

Уравнение статического режима для формы (3)-(4)

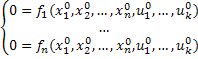
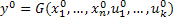, где 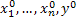- установившиеся значения, переменных состояния и выхода .

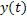2. Передаточной функцией звена (системы) от данного входа 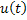к выходу 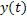называется отношение изображений по Лапласу выходной переменной к входной переменной при нулевых начальных условиях и равенстве нулю прочих входов:

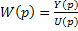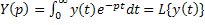, где и 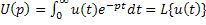(преобразования Лапласа)

3. Детализированной структурной схемой (ДСС) называется алгебраизированная структурная модель САУ, состоящая только из элементарных звеньев типа: а) интегрирующего 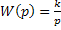; б) дифференцирующего 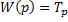; в) безынерционного 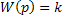; г) нелинейного 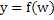с полностью вскрытыми связями между ними.

Пример. Нелинейная электромагнитная цепь:

Где 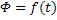- магнитный поток 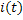- ток, 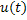– напряжение, 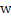– число витков.

Ур-е: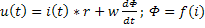

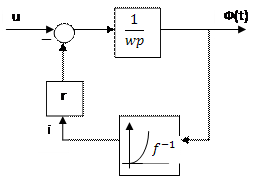ДСС:

ДСС удобны для перехода к дифференциальным уравнениям.

Связь моделей: зная модель в одной форме можно выписать любую другую. Например, по дифференциальному уравнению можно записать ПФ.

1) Переходной характеристикой h(t) звена(системы) называется его реакция на единичное ступенчатое воздействие 1(t):

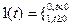
2) Весовой функцией (импульсной характеристикой) w (t) наз. реакция системы на единичную импульсную функцию Дирака δ(t):

;

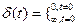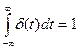
Дата добавления: 2014-01-04