Ексергетичний ККД.Для кількісної оцінки стеупеня термодинамічної досконалості теплового двигуна використовується поняття ексергетичного ККД

А б

Другий закон термодинаміки. Прямі термодинамічні цикли. Термічний ККД. Вічний двигун другого роду. Зворотні термодинамічні цикли. Холодильний коефіцієнт. Прямий та зворотний цикли Карно. Перша теорема Карно. Еквівалентний цикл Карно. Середньоінтегральна температура. Друга теорема Карно. Узагальнений цикл Карно. Принцип регенерації. Науково-практичне значення циклу Карно. Методи порівняння термічних ККД оборотних циклів. Математичний вираз другого закону термодинаміки. Принцип існування та зростання ентропії. Ентропія ізольованої системи. Максимальна корисна робота. Рівняння Гюі-Стодоли. Ексергія та анергія. Ексергія теплоти. Ексергія потоку. Ексергетичний ККД.

Калоричні параметри стану: внутрішня енергія, ентальпія та ентропія, та їх властивості. Термодинамічна робота та її зображення у p – v координатах. Теплота та її зображення у T – s координатах.

Джерела інформації: [1], с.17-32, 46-54, 59-62, 74-78; [2], с.14-24; [8], c.26-27, с.18-20, 22-23, 31-36, 41-43, 49-53, 85-86, 91-98

Калоричні параметри стану: внутрішня енергія, ентальпія та ентропія та їх властивості. До калоричних параметрів стану термодинамічної системи (робочого тіла) відносять внутрішню енергію, ентальпію та ентропію.Енергію хаотичного теплового руху і взаємодії молекул називають внутрішньою енергією U, Дж. Кожна термодинамічна система має запас внутрішньої енергії. Внутрішня енергія, яка віднесена до 1 кг маси тіла, зветься питомою внутрішньою енергією u, Дж/кг. Внутрішня енергія реального газу складається з кінетичної енергії поступального, обертального та коливального рухів молекул, яка залежить тільки від температури робочого тіла, і потенціальної енергії взаємодії молекул між собою, яка залежить від відстані між молекулами, тобто від об'єму робочого тіла. Таким чином внутрішня енергія реального газу є однозначною функцією температури та об'єму: 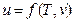або

.

Таким чином, найважливіша властивість питомої внутрішньої енергії – вона є однозначною функцією стану робочого тіла, яка визначається будь-якою парою його основних параметрів 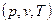, й сама може слугувати параметром стану. Із цього витікає, що зміна внутрішньої енергії не залежить від характеру процесу, а визначається лише початковим та кінцевим станом тіла. Отже, нескінченно малий приріст внутрішньої енергії є повний диференціал , а її зміна у процесі 1-2:

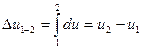
У ідеальному газі сили взаємодії між молекулами відсутні. Тому його внутрішня енергія складається тільки з кінетичної енергії руху молекул і залежить тільки від температури: , або

.

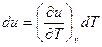Таким чином, зміна внутрішньої енергії ідеального газу у процесі залежить тільки від початкової і кінцевої температури газу. Для кругових процесів (циклів) зміна внутрішньої енергії дорівнює нулю, тобто

.

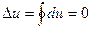Для більшості технічних розрахунків визначення абсолютного значення внутрішньої енергії не потрібне. Необхідно знати лише її зміну, приписавши декотрому стану тіла нульове значення внутрішньої енергії.

Ентальпія 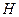, Дж, – функція стану, що дорівнює сумі внутрішньої енергії з добутком абсолютного тиску на об'єм (питома ентальпія , Дж/кг).

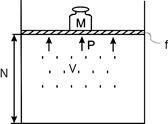Розглянемо повну енергію газу, що знаходиться під тиском 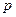, що створюється вагою масою 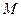(рис. 2.1). Повна енергія системи складається із внутрішньої енергії газу і потенціальної енергії ваги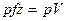

.

Рис.2.1. До пояснення ентальпії

Цю енергію назвали ентальпією. Для 1 кг газу питома ентальпія, Дж/кг, дорівнює

, (2.1)

де 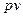– потенціальна енергія тиску.

Питома ентальпія залежить від 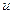, 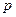і 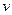і також є параметром стану. Тому зміна 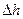, як і зміна 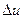, не залежить від характеру процесу, а визначається тільки початковим та кінцевим станом системи, тобто

.

Як однозначна функція стану може бути представлена у вигляді функції будь-якої пари основних парметрів стану, тобто

, , .

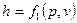Для ідеального газу ентальпія , як і внутрішня енергія , є функцією тільки температури, що витікає з рівняння , звідки . Як і , рахують від декотрого умовного нуля (для газів = 0 при ^оС).

Ентропія , Дж/К – параметр стану, диференціал якого дорівнює відношенню кількості теплоти в елементарному оборотному процесі до абсолютної температури, що є постійною на нескінченно малій ділянці процесу:

. (2.2)

Одиниця виміру питомої ентропії, віднесеної до 1кг речовини, Дж/(кг·К). Ентропія є однозначною функцією стану робочого тіла, яка визначається будь-якою парою його параметрів 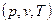. Зміна ентропії у будь-якому процесі визначається лише значеннями параметрів у початковому і кінцевому станах. Ентропія, як і внутрішня енергія та ентальпія, має властивість адитивності: алгебраїчна сума питомих ентропій окремих тіл, що входять до термодинамічної системи, дорівнює питомій ентропії термодинамічної системи у цілому. У технічній термодинаміці необхідно знати лише зміну питомої ентропії у процесі, яка дорівнює

, (2.3)

а ентропії умовно приписують нульове значення, наприклад, при = 0 К. Розвиток поняття про ентропію, як параметр стану, пов'язаний з другим законом термодинаміки. Тому її фізичний зміст буде розкритий пізніше.

Термодинамічна робота та її зображення у p – v координатах. Енергообмін у термодинамічному процесі відбувається за рахунок теплоти або роботи. Робота і теплота – енергетичні характеристики термодинамічного процесу. З математичної точки зору це означає, що елементарні величини роботи та теплоти 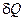не є повні диференціали, а являють собою лише нескінченно малі величини. Таким чином, поза термодинамічним процесом поняття роботи та теплоти не мають змісту. Стану робочого тіла не відповідає яке-небудь значення або .

Механічна робота проти зовнішніх сил, яка пов'язана зі зміною об'єму, визначається виразом

,

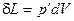а питома робота, яка віднесена до 1 кг речовини, – виразом

, (2.4)

де 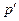– абсолютний тиск (потенціал механічної взаємодії – рушійна сила процесу), віднесений до тиску зовнішнього середовища; 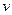– питомий об'єм (координата механічної взаємодії – координата стану, зміна якої характеризує дану форму взаємодії). При рівноважному процесі тиск 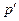у кожний момент часу має дорівнювати тиску робочого тіла 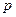; таким чином вираз (2.4) прийме вигляд

, (2.5)

а для кінцевого процесу, при якому об'єм змінюється від до 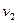, загальний вигляд питомої термодинамічної роботи слід записати таким чином:

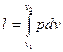. (2.5)

Для визначення інтеграла (2.5) має бути відома залежність 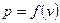. Графічно ця залежність може бути зображена в координатах кривою 1-2 (рис. 2.2). Питома робота зображується в координатах площею, обмеженою кривою процесу, двома ординатами та віссю абсцис, тобто

.

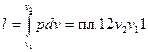Питома робота розширення 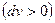має додатний знак, а стиску – від'ємний. Вираз (2.5) відноситься до рівноважних процесів, коли 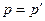, а зміна об'єму відбувається настільки повільно, що усередині робочого тіла не виникає ніяких місцевих відмінностей у тиску, густині та температурі. У реальних необоротних процесах зміна об'єму супроводжується тертям, завихренням і відбувається з кінцевою швидкістю, тому частина роботи витрачається на подолання цих опорів. Тому ефективна питома робота буде меншою за теоретичну, тобто

.

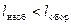Рис. 2.2. Зображення термодинамічної роботи у p – v координатах

Теплота та її зображення у T – s координатах. Теплота – кількісна міра теплової взаємодії робочого тіла з навколишнім середовищем, може бути визначена різними засобами. З (2.2) отримаємо вираз для елементарної кількості теплоти

, (2.6)

а для питомої кількості теплоти

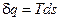. (2.7)

При цьому потенціалом теплової взаємодії є абсолютна температура 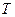, а координатою теплової взаємодії – питома ентропія. Як для роботи зміна об'єму відображає механічну взаємодію робочого тіла з навколишнім середовищем, так і для теплообміну зміна ентропії указує на теплову взаємодію робочого тіла з навколишнім середовищем і визначає знак теплоти: процес збільшення питомої ентропії 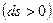означає підведення теплоти від навколишнього середовища до робочого тіла (знак теплоти додатний) і навпаки, зменшення питомої ентропії – відведення теплоти до навколишнього середовища (знак теплоти від’ємний).

Для кінцевого процесу, коли ентропія змінюється від до 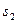, загальний вираз для питомої кількості теплоти має вигляд

. (2.8)

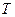Для визначення інтеграла (2.8) треба знати залежність між та – рівняння процесу у координатах (крива 1-2 на рис. 2.3). На діаграмі площа, обмежена кривою процесу та віссю абсцис, зображає питому кількість теплоти

.

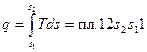Та обставина, що ентропія не піддається безпосередньому вимірюванню, потребує визначення кількості теплоти без застосування поняття ентропії. Історично кількість теплоти визначалась на основі поняття теплоємності (другий спосіб):

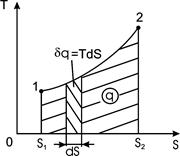
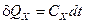або .

де – теплоємність тіла у процесі 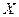(- відношення кількості теплоти 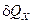у процесі Х до зміни температури тіла у процесі).

Рис. 2.3. Зображення теплоти у T – s координатах

Джерела інформації: [1], с.96-123; [2], с.33-41, 105-109, 140-147; [8], с.46-62.

Другий закон термодинаміки. З першого закону термодинаміки витікає, що взаємоперетворення теплоти і механічної роботи має відбуватися у строго еквівалентних кількостях, тобто те, що теплота і робота кількісно еквівалентні. Але процеси їх взаємоперетворення нерівнозначні, тобто теплота і робота якісно нерівноцінні. Крім того перший закон не встановлює умов, при яких можливі перенесення теплота та взаємоперетворення теплота та роботи. Відмінність теплоти та роботи встановлює другий закон термодинаміки. Він дозволяє указати спрямованість теплових потоків та виявити максимально можливу межу перетворення теплоти в роботу в теплових машинах.

З досвіду відомо, що теплота довільно передається тільки від більш нагрітих тіл до менш нагрітих. Однак можливий і зворотний недовільний процес передачі теплоти від менш нагрітих тіл до більш нагрітих (наприклад, в холодильних установках), але для здійснення його потрібно підведення енергії ззовні для компенсації протікання процесу. Констатація цієї особливості теплоти, яка виявляється у процесі її передачі, є однією з сторін сутності другого закону термодинаміки: в ізольованій термодинамічній системі теплота від холодного джерела до гарячого не може передаватися без компенсації (формулювання Клаузіуса 1850 р.). Компенсацією при цьому називають додаткові зміни, що відбуваються в системі. Ще одна особливість теплоти розкривається при розгляді процесів перетворення теплоти у роботу. Досвід показує, що робота може бути повністю перетворена у теплоту, наприклад, за допомогою тертя, без якої-небудь компенсації. Однак теплоту повністю перетворити в роботу неможливо і для цього перетворення потрібен додатковий довільний компенсаційний процес (відведення частини теплоти до холодного джерела).

Прямі термодинамічні цикли. Прямі цикли здійснюються робочим тілом у теплових двигунах в процесах перетворювання теплоти в роботу. Як показав досвід, всі без виключення теплові двигуни повинні мати гаряче джерело теплоти, робоче тіло, яке здійснює замкнутий процес – цикл, і холодне джерело теплоти.

В існуючих теплових двигунах гарячим джерелом слугують хімічні реакції спалювання палива або внутрішньоядерні реакції, а в якості холодного джерела використовується навколишнє середовище – атмосфера. Роботу двигуна покажемо на і діаграмах (рис. 5.1). Для отримання роботи з теплоти необхідно періодично повторювати процес розширення , тобто повертати робоче тіло у початковий стан. Це можна здійснити у процесі стиснення з витратою роботи . Якщо робота розширення (площа ) більше за роботу стиснення (площа ), то виконується корисна робота . Ця робота відповідає площі , яка обмежена замкнутою кривою обох процесів (рис. 5.1, а). Такий замкнутий процес називається циклом або круговим процесом. Описаний цикл є прямим, бо здійснюється в напрямі руху годинникової стрілки. Якщо зобразити прямий цикл на діаграмі (рис. 5.1, б), процес буде супроводжуватись збільшенням ентропії і підведенням теплоти q ₁, а процес– зменшенням ентропії і відведенням теплоти .

Отже для здійснення прямого кругового процесу у теплових двигунах необхідно поряд з підведенням теплоти від гарячого джерела до робочого тіла відводити теплоту до холодного джерела, тобто необхідно мати різницю температур для здійснення додаткового довільного компенсаційного процесу переходу частини теплоти до холодного джерела. Тому тільки частина витраченої теплоти корисно використовується для отримання роботи , яка у відповідності до першого закону термодинаміки дорівнює (– еквівалентна площі на діаграмі):

.

Ця рівність є математичним виразом принципу еквівалентності теплоти і роботи.

Рис. 5.1. Прямий круговий процес в p-v координатах (а) і T-s координатах (б)

Термічний ККД. Відношення корисної питомої роботи , отриманої в циклі, до питомої теплоти , витраченої у циклі, називається термічним коефіцієнтом корисної дії (ККД) циклу:

. (5.1)

Термічний ККД характеризує ступінь досконалості циклу теплового двигуна. Повністю перетворити теплоту в роботу у кругових процесах неможливо. Частина теплоти має бути віддана холодному джерелу. Тому завжди менше за одиницю.

Отже другий закон термодинаміки можна сформулювати так: для отримання роботи з теплоти необхідно мати різницю температур (формулювання С. Карно 1824 р.). Ще одне формулювання (Планка 1897 р.): неможливо побудувати періодично діючий тепловий двигун, єдиним результатом якого було б охолодження гарячого джерела теплоти та виконання роботи, необхідно додатково віддавати теплоту холодному джерелу.

Вічний двигун другого роду. Тепловий двигун, який працює тільки з одним гарячим джерелом теплоти, називається вічним двигуном другого роду. Тому другий закон термодинаміки можна сформулювати так: вічний двигун другого роду неможливий. Нагадаємо, що вічний двигун першого роду здатний виконувати більше роботи порівняно з еквівалентною кількістю теплоти, що надходить ззовні. Дійсно, якщо припустити створення двигуна, який працював би тільки за рахунок охолодження тепловіддавача, то, використовуючи запаси внутрішньої енергії атмосфери або океану, можна було б отримати практично невичерпну кількість енергії.

Зворотні термодинамічні цикли. Цикл можна здійснити і в зворотному напрямі проти руху годинникової стрілки. Такий цикл називається зворотним. Зворотні цикли здійснюються робочим тілом у холодильних машинах при переходах теплоти від холодного тіла до теплішого, коли компенсуючим є процес перетворення роботи в теплоту. Зобразимо такий цикл у і координатах (рис. 5.2). У цьому випадку питома робота стиснення на ділянці (рис. 5.2, а) буде більше за роботу розширення на ділянці на значення , яке визначається замкнутою лінією . Оскільки чисельно більше і має від'ємний знак, значення буде також від'ємним (робота витрачається ззовні).

Розглядаючи цей цикл на діаграмі (рис. 5.2, б), бачимо, що на ділянці теплота підводиться до робочого тіла від джерела з більш низькою температурою, а на ділянці відводиться в кількості до інших тіл, які мають більш високу температуру. Так передається теплота з нижчого температурного рівня на вищий і відбувається охолодження тіл, яке обов'язково супроводжується витратою (компенсацією) ззовні роботи і перетворенням її в теплоту . При цьому теплота, яка передається на більш високий рівень, дорівнює:

.

а б

Рис. 5.2. Зворотний круговий процес в p-v координатах (а) і T-s координатах (б)

Холодильний коефіцієнт. Ефективність зворотного циклу, за яким працюють холодильні машини, оцінюється холодильним коефіцієнтом, який є відношенням кількості теплоти (холодопродуктивності), що відбирається від охолоджуваного середовища, до затраченої роботи :

. (5.2)

Прямий цикл Карно. Відповідно до другого закону термодинаміки для здійснення термодинамічного циклу потрібно мати як мінімум два джерела теплоти: гаряче (тепловіддавач) з постійною температурою Т ₁ та холодне (теплоприймач) з постійною температурою Т ₂ < Т ₁. При цьому та виконанні умов оборотності підведення теплоти у циклі може здійснюватися тільки за ізотермам Т ₁ і Т ₂. Однак дві ізотерми не можуть утворювати круговий процес. Оскільки інших зовнішніх джерел теплоти немає, оборотний перехід між Т ₁ і Т ₂ можливий лише за адіабатами 2-3 і 4-1 (рис. 5.3). Отже, найпростіший оборотний цикл має складатися з двох ізотерм (1-2, 3-4) та двох адіабат (2-3, 4-1). Такий цикл з двома джерелами теплоти вперше був запропонований французьким інженером С. Карно (1824р.) і в його честь названий циклом Карно. З рис. 5.3 випливає, що питома кількість підведеної у циклі теплот

,

а питома кількість відведеної теплоти

.

Тоді термічний ККД циклу Карно у відповілності до виразу (5.1)

. (5.3)

Рис. 5.3. Прямий цикл Карно в p-v координатах (а) і T-s координатах (б).

Таким чином, термічний ККД циклу Карно залежить лише від абсолютних температур гарячого та холодного джерел теплоти і не залежить від властивостей робочого тіла, тобто не залежить від того, буде робочим тілом ідеальний газ або будь-який інший газ. Це положення носить назву першої теореми Карно. З (5.3) випливає, що ККД циклу Карно тим більше, чим вище Т ₁ і нижче Т ₂.

Зворотний цикл Карно. У цьому циклі, який здійснюється проти напряму руху годинникової стрілки (рис. 5.4), робоче тіло стискається спочатку по адіабаті 3-4 з витратою зовнішньої роботи l ₁, потім по ізотермі 4-1 з відведенням теплоти q ₁ верхньому джерелу. Після цього відбувається розширення робочого тіла спочатку по адіабіаті 1-2 з віддачею зовнішньої роботи l ₂ і зниженням температури від Т ₁ до Т ₂, потім по ізотермі 2-3 з відведенням від нижчого джерела (холодильника) теплоти q ₂. Теплота від холодного тіла передається до більш теплого за рахунок витрати ззовні роботи , яка еквівалентна площі прямокутника 34123. Такий процес не суперечить другому закону термодинаміки, тому що протікає не довільно, а супроводжується додатковим процесом перетворення роботи у теплоту. Холодильний коефіцієнт зворотного циклу Карно

(5.4)

З (5.4) витікає, що збільшення ефективності холодильних установок пов’язане зі зниженням температури навколишнього середовища Т ₁ і підвищенням температури охолоджуваного приміщення Т ₂, тобто зі зниженням різниці температур Т ₁- Т ₂.

Рис. 5.4. Зворотний цикл Карно

Еквівалентний цикл Карно. Цикл Карно має велике значення для теорії теплових двигунів. З рівняння (6.1) витікає, що ККД циклу Карно тим більше, чим вище температура тепловіддваача Т ₁ і чим менше температура теплоприймача Т ₂. Це основне положення, яке витікає з аналізу циклу Карно, як буде показано нижче, дійсне і для будь-якого циклу теплового двигуна. Кожний довільний цикл АВСD, в якому підведення і відведення теплоти відбувається при змінних температурах, можна замінити еквівалентним циклом Карно 1234, де кількості теплоти q₁, q ₂ і зміна ентропії відповідають циклу ABCD (рис. 5.5). З урахуванням того, що

; (5.5)

, (5.6)

термічний ККД довільного циклу ABCD

, (5.7)

Рис. 5.5. Еквівалентний цикл Карно

де і – середні термодинамічні температури, які відповідають процесам підведення та відведення теплоти і у відповідності до (5.5) і (5.6) дорівнюють

; . (5.8)

Ці температури визначаються як висоти прямокутників, однакових за площею з фігурами s ₁ ABC s₂ та s₂ CDA s₁. Інтеграли у (5.8) рахують чисельними або графічними методами, тому і іноді звуть середніми інтегральними або середніми планіметричними температурами.

Таким чином, середня термодинамічна температура – це така умовна температура еквівалентного ізотермічного процесу, в якому кількість теплоти і зміна ентропії відповідно однакові з процесом, що розглядається.

Отже для підвищення термічного ККД будь-якого циклу необхідно підвищувати середню температуру у процесі підведення теплоти і зменшувати середню температуру у процесі відведення теплоти . У цьому полягає важливе практичне значенняциклу Карно.

Межою термічного ККД довільного циклу, який здійснюється між крайніми температурами і , є термічний ККД циклу Карно (див. рис. 5.5) при і . Таким чином, у даному інтервалі температур цикл Карно має найбільшу ефективність (друга теорема Карно). З цього випливає, що ступінь досконалості довільного циклу можна встановити, якщо порівняти його термічний ККД з ККД циклу Карно, який здійснюється між крайніми температурами довільного циклу. В цьому полягає наукове значення циклу Карно.

Узагальнений (регенеративний) цикл Карно. У визначеному інтервалі температур від до найвищий ККД має не тільки цикл Карно, але й будь-який цикл, що складається з двох ізотерм АВ і СD (рис. 5.6). Для цього необхідно, щоб під час протікання процесу ВС теплота від робочого тіла передавалась не зовнішньому теплоприймачу, а через допоміжний теплообмінник (регенератор) поверталась робочому тілу у процесі його нагрівання DA. З зовнішніми джерелами теплоти робоче тіло пов'язане тільки на ділянках АB і СD циклу. Криві процесів BC і DA у діаграмі T - s мають знаходитись на однаковій відстані одна від одної (мають бути еквідистантними), тому , а питома кількість теплоти регенерації у цих процесах однакова, але протилежна за знаком. Таким чином, питома кількість зовнішньої теплоти і у циклі ABCD та ж сама, що і в циклі Карно АВ 21 А. При рівності і будуть рівні і термічні ККД циклів, тобто

.

Цикл ABCD називається ще гранично-регенеративним. Принцип регенерації, як метод підвищення термодинамічної ефективності циклів, широко застосовується у теплосилових і холодильних установках. Звичайно доводиться обмежуватись частковою регенерацією, але й це дає істотне підвищення ефективності циклів.

Рис. 5.6. Узагальнений цикл Карно

Математичний вираз другого закону термодинаміки. Принцип існування та зростання ентропії. Аналітичний вираз , за допомогою якого ентропія була визначена як калоричний параметр стану, якісно пов'язує її зміну з кількістю теплоти і слугує математичним виразом другого закону термодинаміки для оборотних термодинамічних процесів:

. (5.9)

Для необоротних термодинамічних процесів, в яких частина роботи, що витрачається на подолання опорів, обов'язково перетворюється в теплоту , з урахуванням першого закону термодинамікизміна ентропії

, (6.0)

де – питома зовнішня теплота у процесі. З порівняння виразів (5.9) і (6.0) виходить, що у випадку необоротних термодинамічних процесів

. (6.1)

Ця нерівність називається принципом зростання ентропії. Поєднавши (5.9) і (6.1), отримаємо

, (6.2)

або

, (6.3)

тобто у випадку оборотних термодинамічних процесів зміна ентропії дорівнює приведеній теплоті , а у випадку необоротних процесів зміна ентропії більше приведеної теплоти. Вираз (6.3) називають математичним виразом другого закону термодинаміки, де знак рівності відноситься до оборотних термодинамічних процесів, а знак нерівності – до необоротних.

Необоротність завжди призводить до збільшення ентропії робочого тіла і втрати частини роботи. Отже зміна ентропії у необоротних процесах у порівнянні з приведеною теплотою слугує мірою необоротності таких процесів. Для кругових процесів із виразу (6.3) виходить

.

Цей інтеграл у термодинаміці відомий як інтеграл Клаузіуса. Тут температура відноситься до джерел теплоти, а не до робочого тіла. Таким чином, алгебрична сума приведених теплот для будь-якого оборотного циклу дорівнює нулю (– перший інтеграл Клаузіуса), а для необоротного циклу – менше за нуль (– другий інтеграл Клаузіуса).

Ентропія ізольованої системи. Якщо термодинамічні процеси протікають у адіабатній ізольованій системі , то у відповідності до математичного виразу другого закону термодинаміки (6.2)

,

тобто питома ентропія ізольованої системи при протіканні оборотних термодинамічних процесів незмінна (), а при протіканні необоротних процесів зростає . Всі реальні довільні термодинамічні процеси, які протікають у ізольованій системі, необоротні, тому вони призводять до зростання ентропії. Це положення представляє собою найбільш загальне формулювання другого закону термодинаміки для необоротних процесів, відоме під назвою принципу зростання ентропії. Якщо від системи відводиться теплота, то її ентропія може зменшуватися, однак сумарна зміна ентропії системи та ентропії зовнішніх тіл завжди додатна (або дорівнює нулю при оборотних рівноважних процесах у системі). Коли ізольована система знаходиться у стані з максимальною ентропією, у ній не можуть протікати ніякі довільні процеси. Тому стан ізольованої системи з максимальною ентропією є станом її стійкої рівноваги.

Максимальна корисна робота. Ексергія та анергія. Рівняння Гюі-Стодоли. Усяка необоротність призводить до зменшення корисної роботи, тому збільшення ентропії ізольованої системи внаслідок необоротності термодинамічних процесів, що протікають в ній, може слугувати мірою втрати максимально корисної роботи L _max, яку могла б здійснити система при протіканні у ній оборотних термодинамічних процесів. Дійсно, при необоротних процесах утрачена робота довільно перетворюється у теплоту, яка також довільно переходить до тіл з більш низькою температурою, збільшуючи їх ентропію (а отже, і системи) на . Ураховуючи, що теплота дорівнює добутку абсолютної температури на зміну ентропії, необоротне перетворення роботи у теплоту дорівнює

, (6.4)

де – нижча температура в ізольованій системі (при аналізі термодинамічних процесів в якості такої температури приймають температуру навколишнього середовища); – збільшення ентропії ізольованої системи внаслідок необоротності процесів у ній.

Вираз (6.4) характеризує втрату максимальної роботи (працездатності) внаслідок необоротності і носить назву рівняння Гюі-Стодоли. Тоді фактично корисна робота з урахуванням (6.4)

(6.5)

Максимально можлива робота, яку може здійснити система, що складається з джерела енергії та навколишнього середовища, називається ексергією . Таким чином, вираз (6.4) є втратою ексергії внаслідок необоротності процесів.

За смислом другого закону термодинаміки розрізняють види енергії (механічна, електрична та інші), які можуть повністю перетворюватися у інші її види (безмежно перетворювані види енергії), тобто такі, які складаються тільки з ексергії. Відносно теплоти як енергії молекулярно-хаотичного руху, то вона навіть теоретично не може бути повністю перетворена в роботу (неминучий відвід частини теплоти q ₂ до холодного джерела) і, отже, складається з перетворюваної частини (ексергії) і неперетворюваної частини, яку назвали анергія. Так, внутрішня енергія навколишнього середовища або теплота при температурі навколишнього середовища не можуть бути перетворені у інший вид енергії і складаються тільки з анергії. Тому другий закон термодинаміки можна сформулювати ще так: теплота складається з ексергії та анергії. Поняття ексергії широко використовують при аналізі ступеня термодинамічної досконалості окремих процесів, установок та їх елементів.

Ексергія теплоти. Працездатністю (або ексергією ) теплоти , що відбирається від гарячого джерела з температурою , називається максимальна корисна робота, яка може бути отримана за рахунок цієї теплоти при умові, що холодним джерелом є навколишнє середовище з температурою . Корисною називається та частина роботи, яка може бути використана за нашим розсудом.

Максимальна корисна робота теплоти представляє собою роботу рівноважного циклу Карно, що здійснюється у діапазоні температур –:

(6.6)

Таким чином, ексергія теплоти , тобто працездатність теплоти тим більше, чим менше відношення / . При = ексергія теплоти дорівнює нулю.

Ексергія потоку робочого тіла. Визначимо можливий рівноважний шлях переходу потоку робочого тіла з початкового стану 1 з тиском і температурою до кінцевого стану 0 з параметрами навколишнього середовища і . Оскільки система має тільки одне джерело теплоти (навколишнє середовище), рівноважний процес переходу можна уявити собі лише при відсутності теплообміну між потоком і середовищем (адіабатне розширення чи стиснення) або при наявності теплообміну між потоком і середовищем, але обов’язково при температурі (ізотермічне розширення або стиснення). Це означає, що єдиним можливим шляхом переходу до рівноваги з навколишнім середовищем є адіабатне розширення до , і наступне ізотермічне розширення (або стиснення) до , . У останньому процесі робоче тіло відбирає від середовища питому теплоту . Згідно до рівняння першого закону термодинаміки для потоку у випадку, коли і ,

Величина є максимальна питома технічна робота, яку може здійснити робоче тіло у потоці в процесі рівноважного переходу зі стану , , в якому ентропія дорівнює , а ентальпія h ₁, до стану навколишнього середовища , з ентропією і ентальпією . Вона називається максимальною питомою роботоздатністю або питомою ексергією потоку робочого тіла :

(6.7)

(6.8)

де – корисна робота; і – ексергія потоку робочого тіла відповідно на вході до теплового двигуна та на виході з нього, яка визначається за (6.10); – ексергія теплоти, що підводиться до двигуна за (6.9).

Втрата працездатності у тепловому двигуні

До величини входять втрати працездатності, зумовлені тертям і теплообміном при скінченній різниці температур (від внутрішньої та зовнішньої необоротності), а також втрати теплоти двигуном внаслідок теплообміну з навколишнім середовищем. Якщо в технічному пристрої (наприклад, теплообмінному апараті) корисна робота не виконується, то його ексергетичний ККД визначається відношенням зміни питомої ексергії потоку, що нагрівається, до зміни питомої ексергії гріючого потоку

.

Ексергетичні показники можна легко пов’язати з техніко-економічними, оскільки ексергія, як і вартість, може створюватись і знищуватись на протилежність енергії, яка не може ні створюватися, ні знищуватися.

Дата добавления: 2014-01-04