Тепловое излучение

Тепловое излучение – это излучение электромагнитных волн атомами и молекулами тел за счет энергии теплового движения. Тепловое излучение, как и тепловое движение, существует при температуре выше абсолютного нуля. Тепловое излучение, в отличие от других видов излучения, например люминесценции, является равновесным. То есть при тепловом равновесии изолированной системы тел, они могут обмениваться тепловым излучением при одинаковой постоянной температуре сколь угодно долго без подвода энергии извне.

1. Параметры теплового излучения

1. Энергия излучения W – энергия, излучаемая телом со всей поверхности за время наблюдения. 2. Поток излучения 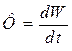– это мощность излучения со всей поверхности тела, равная энергии излучения в единицу времени. В системе СИ измеряется в ваттах (Вт). 3. Энергетическая светимость 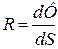– мощность, излучаемая единицей площади поверхности тела. Единица измерения Вт/м2. 4. Спектральная плотность энергетической светимости 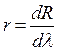. Другое её название – испускательная способность. Она характеризует распределение излучения по длинам волн и равна мощности излучения с единицы площади тела в единичном интервале длин волн. Единица измерения Вт/м3. 5. Тепловое излучение, падающее на непрозрачное тело, может отражаться от поверхности тела, либо поглощаться. Характеристикой поглощения служит поглощательная способность 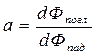. Она равна отношению поглощенного потока к падающему на тело потоку. Согласно определению поглощательная способность не может быть больше единицы.

Особое место в теории теплового излучения занимает абсолютно черное тело, которое полностью поглощает падающее на него излучение, его поглощательная способность равна единице, а = 1 во всех диапазонах длин волн. Таких тел в природе нет. Даже у сажи а = 0,98. Моделью абсолютно черного тела может служить поверхность небольшого отверстия в полости, так как луч света, попав в полость, после многократных отражений исчезает. Если поглощательная способность тела одинакова во всем интервале длин волн и меньше единицы, то такое тело называется серым. Для зеркальной поверхности, а = 0. Для цветных тел поглощательная способность различна в разных диапазонах длин волн. Например, красное тело в большой степени поглощает синие –зеленые участки спектра, но отражает красные лучи.

.

2. Закон Кирхгофа

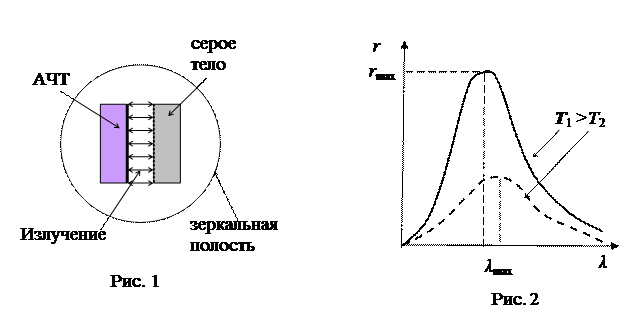
Представим внутри зеркальной оболочки, которая не поглощает, а полностью отражает излучение, несколько тел. Со временем устанавливается температурное равновесие, которое может длиться вечно. Если у некоторого тела поглощательная способность больше, то оно поглощает больше теплоты. Но при равновесии оно должно отдать больше теплоты, то есть энергетическая светимость должна быть пропорциональна его поглощательной способности. Пусть два тела: абсолютно черное и серое обмениваются теплотой в форме теплового излучения (рис. 1).

Теплота, получаемая серым телом от абсолютно черного тела за время t в интервале длин волн Δλ с площади S равна 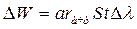. Такое же количество теплоты серое тело должно излучать 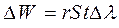. После сокращения, получим 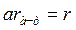. Отсюда следует закон Кирхгофа: отношение спектральной плотности энергетической светимости тела к его поглощательной способности не зависит от природы тела и является универсальной функцией длины волны и температуры.

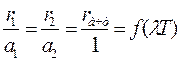. (1)

Например, при одинаковой температуре около тысячи Кельвин, кусок черного угля ярко светится, а белый мел или прозрачное стекло почти не излучают.

Так как для абсолютно черного тела а = 1, то универсальная функция Кирхгофа имеет смысл спектральной плотности энергетической светимости абсолютно черного тела rачт= f(λ,T). Она зависит от от длины волны и температуры (рис. 2).

Формула функции Кирхгофа было получено М. Планком в 1900 г. При выводе впервые в истории науки Планк ввел понятие о квантовании энергии излучения атомов: e = h n, где h = 6,63 10-34Дж с – постоянная Планка, n – частота излучения. Формула Планка идеально совпала с экспериментальной зависимостью спектральной плотности энергетической светимости для абсолютно черного тела (рис.1):

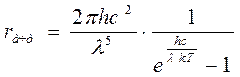. (2)

3. Экспериментальные законы теплового излучения

Формула Планка подтвердила ранее установленные экспериментальные законы теплового излучения абсолютно черного тела. Согласно определению энергетическая светимость связана со спектральной плотностью энергетической светимости соотношением 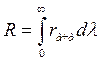. Если проинтегрировать формулу Планка, то будет подтвержден закон Стефана – Больцмана: энергетическая светимость абсолютно черного тела пропорциональна четвертой степени абсолютной температуры

R = s T 4, (5)

где s = 5,67 10 –8 Вт/м 2К 4 – постоянная Стефана – Больцмана.

Для серого тела, подставив в интеграл r = a∙rачт согласно закону Кирхгофа, получим, что энергетическая светимость меньше в а раз, чем для абсолютно черного тела:

R cт = a s T 4. (3)

Закон смещения Вина определяет положение максимума функции Кирхгофа: длина волны, на которую приходится максимум спектральной плотности энергетической светимости абсолютно черного тела, обратно пропорциональна его абсолютной температуре:

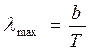, (4)

где постоянная Вина b = 2898 мкм/К. С повышением температуры излучение тела смещается в диапазон все более коротких волн.

Второй закон Вина определяет высоту максимума функции Кирхгофа: максимальная спектральная плотность энергетической светимости абсолютно черного тела пропорциональна пятой степени температуры:

r max= С Т 5, (5)

где постоянная С = 1,3 10 –5 Вт/м 3 К 5.

5. Пирометры

Параметры теплового излучения тел зависят от температуры. Это позволяет создать приборы бесконтактного способа измерения температуры тел по их тепловому излучению. Такие приборы называются пирометрами. Для тел с температурой несколько тысяч кельвин это единственный способ измерения. Существует три вида пирометров: радиационные, цветовые и яркостные пирометры.

1. Наиболее простым типом пирометра является яркостной пирометр с исчезающей нитью. Принцип действия прибора основан на сравнении яркости излучения исследуемого тела с яркостью нити накала эталонной лампы пирометра. Яркость излучения нагретого тела пропорциональна его энергетической светимости и, согласно закону Стефана – Больцмана, зависит от его температуры. Глаз человека способен воспринимать излучение тел с температурой 800 оС и выше. В этом же интервале температур применяются яркостные пирометры.

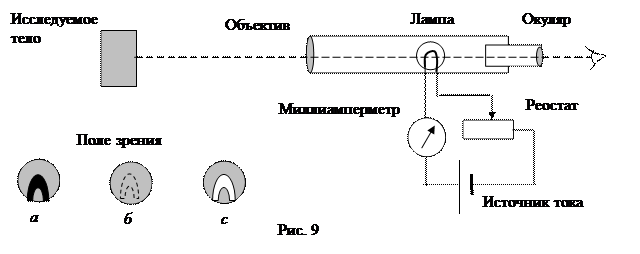
Пирометр представляет собой зрительную трубу с объективом для фокусировки изображения исследуемого тела и окуляром для фокусировки изображения нити эталонной лампы (рис. 10.9). Яркость нити накала и сила тока регулируется реостатом и измеряется миллиамперметром. Шкала миллиамперметра предварительно про-градуирована в единицах температуры по яркости излучения абсолютно черного тела. Абсолютно черным телом может служить небольшое отверстие в полости нагреваемого тела, температура которого контролируется, например, с помощью термопары.

В процессе измерения следует так изменять силу тока лампы, чтобы изображение нити исчезло на фоне исследуемого тела (рис. 9, б). После этого определить так называемую яркостную температуру по шкале миллиамперметра. Так как исследуемые тела обычно не являются абсолютно черными, то их истинная температура выше измеренной яркостной температуры. Поэтому следует добавлять к измеренной яркостной температуре положительную поправку.

Для определения поправки подставим в закон Кирхгофа формулу Планка. Так как измеряемые температуры достаточно велики, то единицей в знаменателе можно пренебречь: 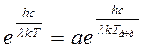. Логарифмируя, получим

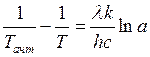. (6)

Отсюда по измеренной пирометром температуре абсолютно черного тела можно определить истинную температуру, рассчитать яркостную поправку, создать таблицы или построить график поправок для тел с различным значением поглощательной способности для заданной длины волны. Обычно используется встроенный в пирометр светофильтр для длины волны 660 нм. Можно переградуировать пирометр для конкретного объекта, контролируя его температуру другим способом, например термопарой.

2. Для бесконтактного измерения температур -50 – 300 оС и выше применяются радиационные пирометры. Например, при измерении температуры букс колесных пар. В этом интервале температур излучение тел, согласно закону Вина, приходится на инфракрасное излучение с длиной волны несколько микрометров, которое не воспринимается глазом человека.

Приемниками инфракрасного излучения такого диапазона являются термостолбики и болометры. Инфракрасное излучение нагревает чувствительный элемент болометра (пленка полупроводника или металла) и его сопротивление изменяется. Это приводит к изменению силы тока, которое после усиления регистрируется индикатором. Термостолбик представляет собой большое количество термопар, соединенных последовательно. Термопара состоит из двух разнородных проводников, спаянных на одном конце, а другие концы подсоединяются к измерительному прибору. Инфракрасное излучение нагревает спаи термопар, в результате чего возникает термоЭДС, которая пропорциональна повышению температуры облучаемых спаев термопар.

Радиационный пирометр представляет собой зрительную трубу. С помощью линзы или сферического зеркала изображение исследуемого объекта фокусируется на болометр или спаи термопар (рис11). При постоянном телесном угле зрения γ наблюдаемая площадь, с которой излучается тепловой поток Ф=RS, растет пропорционально квадрату расстояния между объектом и пирометром: 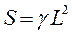. Но одновременно уменьшается обратно пропорционально квадрату расстояния телесный угол, в котором распространяется часть потока, попадающая во входное отверстие пирометра: 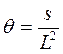. В итоге поток, попадающий во входное отверстие пирометра 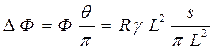, не зависит от расстояния между объектом и пирометром. Но при условии, пока объект полностью попадает в поле зрения пирометра и его изображение перекрывает чувствительный элемент болометра полностью.

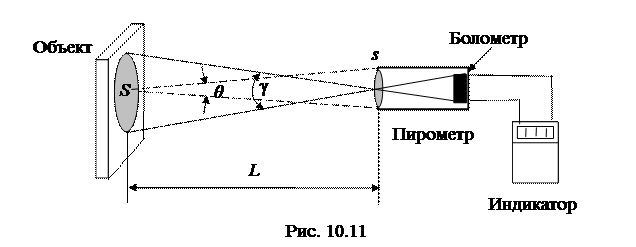
Предварительно пирометр и его индикатор калибруют по излучению абсолютно черного тела. Если исследуемый объект не является абсолютно черным, то индикатор регистрирует так называемую радиационную температуру. Она меньше истинной температуры. Приравнивая энергетические светимости абсолютно черного тела и исследуемого объекта, согласно закону Стефана – Больцмана, 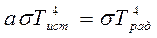, получим для истинной температуры формулу

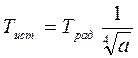. (10.8)

Обычно поглощательная способность объекта может быть неизвестна. Например, для стальных, окисленных букс она может быть около 0,6. Но корень четвертой степени будет уже 0,9. Значит, погрешность измерения будет около 10% и в этом случае следует ввести поправку. Для удобства наведения на объект радиационный пирометр снабжают лазерным указателем.

4. Источники светового и теплового излучения

5. ФОТОНЫ

Атомы, оказавшись в возбужденном состоянии вследствие теплового движения, или под действием электрического поля, удара другого атома и т.д., излучают избыток энергии в виде электромагнитной волны. Время излучения составляет менее 10-8 с, и поэтому электромагнитная волна имеет ограниченные размеры. Распространяясь в пространстве и взаимодействуя с веществом, она ведет себя не только как волна, но и как частица, корпускула. Такие частицы названы фотонами. Корпускулярные свойства света проявляются в таких экспериментах как внешний и внутренний фотоэффект, давление света, эффект Комптона и других опытах.

1. Корпускулярные параметры фотонов

Энергия фотона, как установил Планк, равна произведению постоянной Планка на частоту излучения

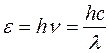, (7)

где h =6,63∙10-34 Дж∙с, λ – длина волны.

Масса фотона. Так как по своей природе фотон это электромагнитная волна, которая не может находиться в покое, то масса покоя фотона равна нулю. При распространении фотон обладает энергией. По уравнению Эйнштейна эквивалентности между массой и энергией, масса фотона равна отношению энергии фотона к квадрату скорости света

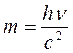. (8)

Импульс фотона. Как и для любого тела, импульс фотона равен произведению массы на скорость, равную скорости света

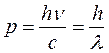, (9)

2. Внешний фотоэффект

Внешний фотоэффект – это явление испускания электронов телами под действием света. Экспериментальное исследование фотоэффекта впервые провел А.Г. Столетов. Вакуумный фотоэлемент (стеклянный баллон с электродами) включался в цепь источника постоянного тока. Катод из исследуемого металла освещался монохроматическим светом. Исследовалась зависимость силы фототока от напряжения (вольтамперная характеристика) (рис.1), от частоты монохроматического излучения (спектральная характеристика), от освещенности.

Рис. 1 Схема установки Столетова

Рассмотрим вольтамперную характеристику (рис. 1). При отсутствии напряжения сила фототока не равна нулю, так как электроны, вылетая из катода при его освещении, образуют электронное облако, из которого они могут попадать на анод и перемещаться по внешней цепи обратно на катод. С ростом прямого напряжения все большая часть электронов под действием электрического поля попадает на анод и сила фототока быстро возрастает. Когда все испускаемые катодом электроны попадают на анод, сила фототока достигает насыщения. Сила тока насыщения равна заряду электронов, испускаемых катодом и попадающих на анод в единицу времени, J = e n.

При смене полярности с ростом напряжения сила фототока падает, так как запирающее электрическое поле препятствует попаданию из электронного облака на анод сначала медленных электронов и, наконец, самых быстрых. Напряжение, при котором сила фототока падает до нуля, называется запирающим. Его величина определяется из закона сохранения энергии: кинетическая энергия самых быстрых электронов расходуется на совершение работы против сил поля

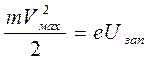. (1)

При изучении зависимости силы фототока от частоты монохроматического света (спектральная характеристика фотоэлемента) обнаружено, что фотоэффект возможен только в диапазоне частот выше так называемой красной границы.

На основании экспериментов Столетов установил законы фотоэффекта. 1. Сила фототока насыщения при освещении катода монохроматическим светом прямо пропорциональна световому потоку. 2. Максимальная кинетическая энергия фотоэлектронов не зависит от освещенности, а линейно зависит от частоты(рис. 2).. 3. Для каждого металла существует так называемая красная граница фотоэффекта, то есть граничная частота, ниже которой фотоэффект не происходит.

Волновая теория света не смогла объяснить законы фотоэффекта. По этой теории электроны раскачиваются в электрическом поле световой волны любой частоты и, набрав за некоторое время достаточно энергии, вылетают из металла. На самом деле фотоэффект практически безинерционен и фотоэффект вызывает сет, частота которого выше граничной частоты. По волновой теории кинетическая энергия должна быть пропорциональна амплитуде напряженности поля, то есть освещенности. На самом деле энергия фотоэлектронов не зависит от освещенности, а только от частоты облучения

Закономерности фотоэффекта объяснила квантовая теория света. По этой теории свет – это поток фотонов, излученных атомами и молекулами вещества. Энергия фотона определяется по формуле Планка, e = h n, где h = 6,63 10 –34 Дж∙с – постоянная Планка, n – частота излучения. При фотоэффекте фотоны, попадая в металл, взаимодействуют с электронами. Это процесс неупругого взаимодействия, после которого фотон, отдав энергию электрону, перестает существовать. Если электрон, получив избыточную энергию, движется к поверхности, то он имеет шанс вылететь за пределы металла. Закон сохранения энергии для фотоэффекта, называемый уравнением Эйнштейна, имеет вид

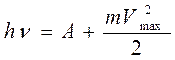, (2)

энергия, полученная электроном от фотона, расходуется им на совершение работы выхода из металла А и на приобретение кинетической энергии.

Работа выхода электрона обусловлена преодолением двойного тормозящего электрического слоя, образованного свободными электронами над поверхностью металла, и взаимодействием с зарядившимся положительно металлом. Не все электроны вылетают с максимальной скоростью. Некоторые теряют часть энергии в поверхностных слоях металла и вылетают с меньшей скоростью. Некоторые, более 99 %, остаются в металле.

Уравнение Эйнштейна объясняет закономерности фотоэффекта. Во-первых, сила фототока насыщения пропорциональна световому потоку, так как пропорционально растет число фотонов. Во-вторых, максимальная кинетическая энергия фотоэлектронов, согласно уравнению Эйнштейна, зависит только от частоты по линейному закону. В-третьих, с уменьшением частоты света, при некоторой так называемой граничной частоте, энергии даже самому быстрому электрону хватает только на то, чтобы выйти за пределы металла. Если частота будет меньше граничной, то энергия электрона будет недостаточна для совершения работы выхода и фотоэффекта не будет

hnгр = А. (3)

Долго квантовая теория фотоэффекта не получала признания научного сообщества того времени, было предложено много волновых теорий явления, но все таки гипотезе квантов победила

Явление фотоэффекта находит широкое применение в автоматике, телемеханике, измерительной технике.

3. Давление света

Так как фотоны обладают импульсом, то при падении на поверхность они действуют на неё с некоторой силой. Пусть направленный пучок света падает перпендикулярно к поверхности. Пусть число фотонов, падающих на поверхность площадью S за время Δt, равно N. Часть фотонов Nρ отражается, где ρ – коэффициент отражения. Применим уравнение второго закона Ньютона к фотонам: изменение импульса фотонов равно импульсу силы, действующей на фотоны со стороны поверхности. В проекции на нормаль к поверхности уравнение примет вид

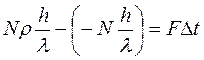
Давление, по определению, равно отношению нормальной составляющей силы давления к площади поверхности 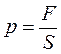. Подставив и преобразовав уравнение второго закона Ньютона, получим

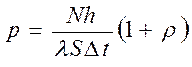. Умножим и поделим правую часть на скорость света: 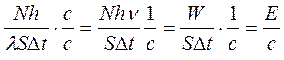. Здесь Е – энергетическая освещенность поверхности, равная отношению энергии падающих фотонов 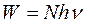к площади поверхности и времени поглощения. В результате преобразований получим расчетную формулу для давления света

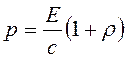
Из формулы следует, что давление на зеркальную поверхность (ρ = 1) в два раза выше, чем на черную поверхность (ρ = 0).

Давление света даже от мощных источников света настолько мало, что ощутить его невозможно. Однако Лебедев экспериментально измерил давление света

Зато внутри звезд давление света поддерживает равновесие, противодействуя гравитационному сжатию.

4. Эффект Комптона

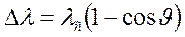
Здесь 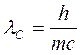=2,43 пм – комптоновская длина волны.

6. БОРОВСКАЯ ТЕОРИЯ АТОМА

1. Опыты Резерфорда

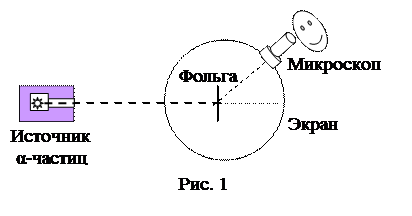Резерфорд и его сотрудники исследовали рассеяние α-частиц при прохождении их через тонкую металлическую фольгу. Альфа частицы – это ядра гелия, испускаемые со скоростью 107 м/с радиоактивными препаратами. После пролета через фольгу α-частицы отклонялись от первоначального направления на различные углы. Рассеянные частицы попадали на экран из сернистого цинка ZnS, вызывая слабую вспышку, которую можно было наблюдать в микроскоп. Воздух из корпуса прибора откачивался.

Оказалось, что некоторые частицы, примерно одна из 2000, отклонялись на очень большие углы, почти в обратном направлении. Резерфорд пришел к выводу, что такое отклонение α-частиц возможно только от заряженного, очень маленького, но массивного ядра. Радиус ядра можно оценить, считая, что кинетическая энергия α-частицы при столкновении превращается в потенциальную электростатическую энергию: 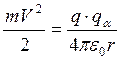. Отсюда размер ядра r=10-14 м.

На основании опытов Резерфорд предложил так называемую планетарную модель атома. По этой модели в центре атома находится ядро с зарядом q = Ze, где Z – порядковый номер элемента в таблице Менделеева. В ядре сосредоточена почти вся масса атома, а вокруг ядра в пространстве, занимаемом атомом, расположены Z электронов.

2. Постулаты Бора

Планетарная модель атома, предложенная Резерфордом, противоречила классической электродинамике, так как электрон, вращаясь с центростремительным ускорением, должен излучать электромагнитные волны. Спектр излучения должен быть сплошным, так как из-за потерь энергии на излучение электрон должен приближаться к ядру с увеличением частоты и, наконец, упасть на ядро. На самом деле атомы вечны, спектр излучения газов не сплошной, а линейчатый. Это значит, что все атомы имеют одинаковый и, главное, дискретный набор энергетических уровней. Для водорода, простейшего из атомов, по экспериментальным данным спектроскопистами была подобрана так называемая сериальная формула Бальмера для частот излучения

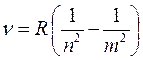(1)

Здесь n и m – целые числа, R = 3,29∙1015 1/c– постоянная Ридберга. Каждому числу n − номеру серии, соответствуют линии с m>n.

Для объяснения устойчивости атома Бор ввел постулаты.

Первый постулат: электроны в атоме могут двигаться только по определенным стационарным орбитам, находясь на которых они не излучают энергии. Эти орбиты определяются условием квантования: момент импульса электрона кратен постоянной Планка, деленной на 2p,

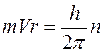. (2)

Здесь r и V – радиус орбиты электрона и его скорость; n = 1, 2, 3,..– главное квантовое число; h = 6,63 10 -34 Дж∙с – постоянная Планка.

Второй постулат: атом излучает квант энергии в виде цуга электромагнитной волны, когда электрон переходит с более высокого уровня энергии (орбиты) «m» на более низкий уровень «n». Излученная энергия равна разности уровней энергии:

hn= Wm – Wn. (3)

Постулаты Бора не следуют из законов классической физики. Это гениальная догадка. Только с созданием квантовой механики было показано, что они являются следствием решения уравнения Шредингера для атома водорода. Теория атома, созданная Бором объяснила устойчивость атома и происхождение линейчатого спектра излучения разреженных газов.

3. Атом водорода в теории Бора

Применение постулатов Бора и уравнения второго закона Ньютона к атому водорода позволяет получить значения частот излучения, с большой точностью соответствующие экспериментальным данным. Произведем этот расчет. Второй закон Ньютона в применении к движению электрона по круговой орбите под действием кулоновской силы имеет вид

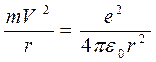. (4)

Решая совместно уравнения (2) и (4), можно получить формулы для радиуса орбиты электрона и его скорости.

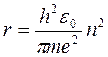
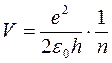
Как видно, радиус орбиты электрона и его скорость могут принимать только дискретный ряд значений при целом значении квантового числа n.

Затем их следует подставить в формулу энергии атома. Полная энергия атома водорода равна сумме кинетической энергии электрона и потенциальной энергии взаимодействия электрона с ядром

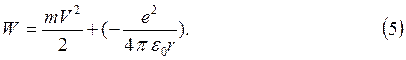
В результате получим:

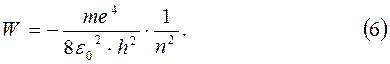
Энергия атома отрицательна и принимает дискретный, квантованный, ряд значений. Обозначим энергию на основном, первом, энергетическом уровне W 1. Для атома водорода она равна W1 = −13,6 эВ. Энергия атома на более высоких уровнях будет обратно пропорциональна квадрату главного квантового числа:

Согласно второму постулату Бора при переходе электрона с более высокой орбиты «m» на более низкую «n» излучается фотон, с энергией hn = Wm − Wn. Подставив сюда формулу (7), получим для частот излучения

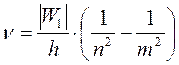. (8)

Это выражение точно совпадает с сериальной формулой (1). Серия спектральных линий атома водорода при n = 1 носит название серии Лаймана, линии этой серии находятся в ультрафиолетовом диапазоне (рис. 1). Серия при n = 2 носит название серии Бальмера. Линии этой серии находятся в диапазоне видимого света: при m =3 – красная, m = 4 – зеленая, m = 5 – фиолетовая. Это соответствует переходам электрона с 3, 4 или 5 орбит на 2-ю орбиту. Линии других серий находятся в инфракрасном диапазоне.

4. Опыт Франка–Герца

Дискретность энергетических уровней атомов была подтверждена в опытах Франка – Герца. В этих опытах электроны в электронной лампе, наполненной исследуемым газом под низким давлением, разогнавшись в электрическом поле, испытывали соударение с атомами.

Возможно два типа соударений. Неупругое соударение происходит, если энергия электрона равна, или достаточно близка, к разности энергий одного из возбужденных состояний и основным состоянием атома. В этом случае атом может принять энергию электрона, происходит резонансное поглощение энергии, и атом переходит в возбужденное состояние. А электрон теряет свою энергию и скорость. Обратный переход возбужденного атома в основное состояние совершается сбросом энергии в виде излучения. Если энергия электрона больше или меньше энергии резонансного поглощения, то соударение электрона с атомом происходит упруго. Без потери энергии электрон отлетает от атома.

Потенциалы электрического ускоряющего поля при резонансном поглощении энергии электронов называются резонансными потенциалами. В электронной лампе, откачанной до глубокого вакуума, с небольшим количеством паров ртути, были расположены электроды (рис. 1). Источником электронов являлся накаливаемый катод. В регулируемом электрическом поле между катодом и первой сеткой электроны разгонялись. В пространстве между сетками происходили соударения электронов с атомами ртути. Между второй сеткой и анодом было создано постоянное сравнительно слабое тормозящее поле. Если происходило неупругое взаимодействие электронов с атомами, то они теряли кинетическую энергию и не могли попасть на анод через тормозящее поле. Сила тока между анодом и катодом резко падала. Если ускоряющее напряжение между катодом и сеткой отличалось от резонансного потенциала, то электроны преодолевали тормозящее поле и попадали на анод. Сила тока возрастала. Сила тока могла падать при ускоряющем напряжении, превышающем потенциал возбуждения в два, три и более раз, так как могло происходить два, три и более соударений.

Характерная вольтамперная характеристика лампы имеет вид кривой с несколькими максимумами тока и минимумами (рис.2). Она подтверждает существование дискретных уровней энергии.

9. ВОЛНОВЫЕ СВОЙСТВА МИКРОЧАСТИЦ

1. Гипотеза де Бройля

Из курса Оптики известно, что свет – это поток фотонов, которые одновременно обладают как волновыми, так и корпускулярными свойствами. Например, если свет очень малой интенсивности, так что фотоны летят по одиночке, пропускать через небольшое отверстие, то все равно на фотопластинке со временем из отдельных засвеченных точек создается система дифракционных колец. Здесь одновременно проявляются волновые свойства фотонов, поскольку это электромагнитные волны, и корпускулярные свойства фотонов.

В 1924 году Луи де Бройль выдвинул гипотезу, что сочетание волновых и корпускулярных свойств присуще не только фотонам, но также микрочастицам вещества, таким как электроны, протоны, атомы и даже молекулам. Причем соотношение между волновыми и корпускулярными свойствами точно такое же, как и для фотонов. Длина волны де Бройля равна отношению постоянной Планка к импульсу частицы, а частота волнового процесса равна отношению энергии частицы к постоянной Планка:

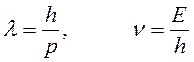, (1)

где импульс нерелятивистских частиц равен произведению массы частицы на скорость .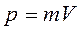

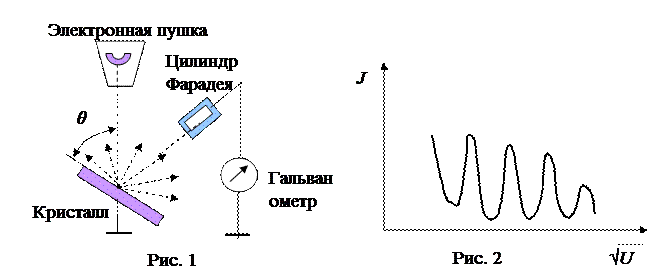
Гипотеза де Бройля была экспериментально подтверждена. В опытах Дэвиссона и Джермера исследовалось отражение электронов от монокристалла никеля. Отраженные электроны улавливались цилиндром Фарадея, расположенного под некоторым углом. Сила тока отраженного пучка регистрировалась гальванометром. Оказалось, что зависимость интенсивности отраженного пучка электронов от ускоряющего напряжения электронной пушки имеет несколько максимумов, разделенными минимумами. Это было похоже на отражение рентгеновских лучей от монокристаллов, которое объясняется явлением дифракции рентгеновских волн. То есть пучок электронов обладает волновыми свойствами.

По закону сохранения энергии скорость электронов зависит от ускоряющего напряжения 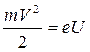. Длина волны по формуле де Бройля будет равна

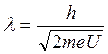. (2)

Оказалось, что рассчитанные значения длин волн электронов совпадают со значениями длин волн рентгеновского излучения, рассчитанными по формуле Вульфа–Брэгга .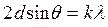

Волновые свойства электронов были обнаружены при прохождении электронов сквозь тонкие пленки поликристаллической структуры Тартаковским и Томсоном. На маленьких кристалликах, происходит дифракция. Так как кристаллики ориентированы хаотично, то дифракционная картина имеет вид колец, как и рентгенограмма.

Вопрос, что обладает волновыми свойствами: пучок электронов или отдельный электрон был решен в опытах Фабриканта на электронном микроскопе. Электроны летели настолько редко, что дифрагировали на выходном отверстии микроскопа поодиночке, и при длительной экспозиции на фотопластинке из отдельных точек возникала система дифракционных колец.

Понятие о волнах де Бройля в развитии современной науки оказалось поворотным пунктом. Исчезла необходимость в постулатах Бора.Например, представим электрон в атоме как стоячую волну де Бройля и пусть как для стоячей волны в струне, на длине орбиты укладывается целое число волн де Бройля: 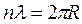. Подставим сюда формулу для длины волны де Бройля и получим постулат Бора: момент импульса электрона кратен постоянной Планка .

.

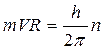2. Принцип неопределенности Гейзенберга

Если микрочастицы обладают свойствами волны, то, как и для волны, нельзя абсолютно точно указать точку локализации волны и ее направление распространения. Чем длиннее волновой цуг, тем точнее определено направление распространения, но тем больше неопределенность положения цуга. И наоборот, чем короче цуг волн, тем точнее определено положение цуга, но больше неопределенность направления распространения (рис. 3).

Рассмотрим в качестве примера дифракцию частицы на узкой щели. Положение частицы в момент прохождения через щель известно с точностью до ширины щели Δх. Но после прохождения щели направление распространения частицы становится неопределенным, где-то в пределах угла расположения хотя бы центрального дифракционного максимума. Появляется неопределенность импульса частицы 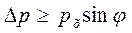. Из теории дифракции для световых волн известно, что угловому положению первого минимума, или краю центрального максимума, соответствует соотношение 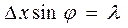. Исключая синус угла φ, подставляя формулу длины волны де Бройля, получим соотношение, называемое принципом неопределенности Гейзенберга

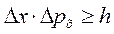. (3)

Произведение неопределенности координаты частицы на неопределенность ее импульса не может быть меньше постоянной Планка. Принцип неопределенности Гейзенберга накладывает принципиальные ограничения на точность одновременного измерения пар величин. Например, чтобы точнее определить положение микрочастицы, наблюдаемой в микроскоп, надо освещать светом как можно меньшей длины волны, так как погрешность измерения равна длине волны. Но чем меньше длина волны фотонов, тем больший импульс они передают микрочастице

Аналогичное соотношение существует для пары величин энергия – время

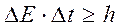. (4)

Произведение времени нахождения частицы в некотором состоянии на неопределенность энергии частицы не может быть меньше постоянной Планка. Для стабильной частицы (Δt →∞) энергия может быть измерена с высокой точностью.

Принцип неопределенности не является применимым только к волнам де Бройля. Аналогичные соотношения существуют в радиотехнике, в акустике при излучении и приеме коротких сигналов. Например, чем короче сигнал, тем больше погрешность с измерения частоты.

Для квантовых микрочастиц неопределенность импульса и энергии сопоставима с самой величиной импульса и энергии. Это позволяет оценивать импульс и энергию частиц с помощью принципа неопределенности.

3. Уравнение Шредингера

Движение свободной, вне силовых полей, частицы описывается уравнением гармонической функции (функции синуса, косинуса, экспоненты с мнимым показателем) для волны де Бройля. Запишем, для удобства преобразований, при движении частицы вдоль координаты х уравнение волны де Бройля в виде экспоненты с мнимым показателем:

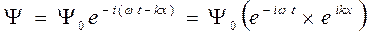. (1)

Часть функции, зависящая от времени, определяет частоту колебаний. Часть, зависящая от координаты х, определяет распределение амплитуды пси-функции по направлению координаты х. Для свободной частицы это уравнение плоской волны 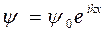. Здесь 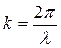– волновой вектор, 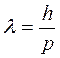– длина волны де Бройля, i – мнимая единица..

Определим вид дифференциального волнового уравнения, решением которого может быть уравнение для амплитуды пси-функции. Для этого достаточно продифференцировать уравнение амплитуды дважды по координате х.: 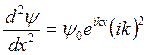. Откуда 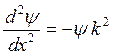. Представим квадрат волнового вектора в виде 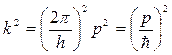и волновое уравнение для амплитуды пси-функции свободной частицы примет вид

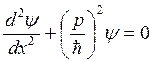. (2)

Преобразуем это уравнение для волны де Бройля свободной частицы в уравнение для движения частицы в силовом поле с потенциальной энергией U, не зависящей от времени. Для этого запишем соотношение между импульсом и кинетической энергией частицы 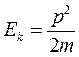. Кинетическую энергию определим как разность между полной и потенциальной энергиями 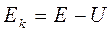. Подставив в волновое уравнение квадрат импульса 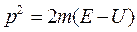, получим

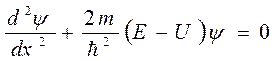. (3)

Это так называемое амплитудное уравнение Шредингера для простейшего случая одномерного движения частицы для стационарных состояний, то есть не зависящих от времени. Здесь m – масса частицы, ħ = 1,056∙10-34 Дж∙с – постоянная Планка.

При движении частицы в произвольном направлении следует определять производную для трех пространственных координат:

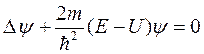. (4)

Здесь 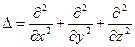символ оператора Лапласа.

Уравнение Шредингера является основным уравнением квантовой механики, подобно уравнениям Ньютона в классической механике.

10. ЧАСТИЦА В ПОТЕНЦИАЛЬНОЙ ЯМЕ

1. Физический смысл квадрата пси-функции

Сопоставим два уравнения: для электромагнитной волны 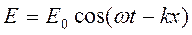и для волны де Бройля 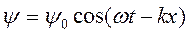. Плотность энергии в электромагнитной волне по волновой теории пропорциональна квадрату напряженности электрического поля: 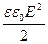, а по корпускулярной теории света плотность энергии пропорциональна плотности потока фотонов 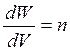. Аналогично квадрат пси-функции будет пропорционален плотности потока частиц. Если рассматривается движение одной частицы, то квадрат пси-функции будет равен плотности вероятности нахождения частицы (то есть вероятности нахождения в единичном объеме) в рассматриваемой точке пространства: 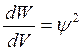. Для определения вероятности нахождения частицы в заданном объеме следует проинтегрировать по объему V. Если пси функция не содержит мнимой части, то .

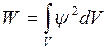Из физического смысла квадрата пси-функции определяются ограничения на возможные решения уравнения Шредингера. Пси-функция должна быть однозначна, ограничена, не иметь разрывов, то есть пси-функция и её первая производная должны быть непрерывны. Должно выполняться условие нормировки: если частица находится в рассматриваемом объеме, то вероятность ее нахождения там равна единице: .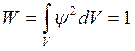

2. Частица в потенциальной яме

Потенциальной ямой называется область пространства, в которой потенциальная энергия меньше, чем в окружающем пространстве. Например, атом для электрона, ядро атома для протонов и нейтронов, объем металла для электронов. Классической потенциальной ямой является обычная яма на поверхности Земли, например для шарика. Но если движение шарика подчиняется законам классической механики Ньютона, то движение электрона в атоме, оказывается, подчиняется не законам Ньютона, а законам квантовой механики. Рассмотрим простейшую задачу квантовой механики о движении частицы в одномерной потенциальной яме с бесконечно высокими стенками.

Пусть частица массы m находится в потенциальной яме шириной l, внутри которой потенциальная энергия равна нулю, а за пределами ямы бесконечно высока (рис. 1). Пусть частица движется вдоль координатной оси х перпендикулярно стенкам. Применим для решения задачи амплитудное уравнение Шредингера

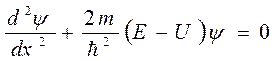. (4)

Чтобы за пределами ямы выполнялось равенство нулю уравнения при бесконечно большом значении потенциальной энергии, приходится положить значение пси-функции вне ямы равным нулю, ψ = 0. То есть появляться за пределами ямы частице запрещено.

Внутри ямы уравнение Шредингера принимает вид 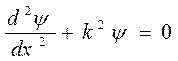. Здесь введено обозначение 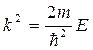. Будем искать решение этого дифференциального уравнения в виде суммы гармонических функций .

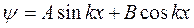Определим постоянные интегрирования А и В. Из условия непрерывности пси-функции на границах ямы пси-функция должна быть равной нулю. Подставив в искомое решение х = 0, получим 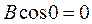, откуда В = 0. Подставив x = l, получим 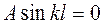. Это возможно, если 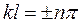, то есть число n = 1, 2, 3…принимает целые значения. Такие решения уравнения Шредингера называются собственными функциями

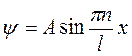. (5)

На рис. 2 изображены графики нескольких собственных функций и их квадратов. Если в классической потенциальной яме шарик с равной вероятностью может оказаться в любом месте ямы, то квантовая частица чаще, с большей вероятностью, находится там, где квадрат пси функции имеет наибольшее значение. Лишь при огромном значении квантового числа n наиболее вероятные положения частицы сближаются, приближаясь к классическому распределению.

Подставим в условие квантования 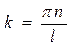соотношение параметра с энергией 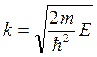, получим самый важный вывод квантовой механики: энергия частицы, запертой в потенциальной яме, может принимать не любые, а только дозволенные значения энергии:

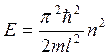(6)

Чем меньше размер потенциальной ямы, тем энергия выше. Например, электрон в атоме (l= 10-10 м) имеет по этой формуле энергию около 10 эВ, а если его локализовать в ядре атома (l =10-14 м), то его энергия должна быть в 108 раз больше. Столь огромной энергией, во много раз большей энергии покоя (109 эВ >> 0,51∙106 эВ), электрон обладать не может и значит внутри ядра он существовать не может.

3. Прохождение частиц через потенциальный барьер

11. АТОМ ВОДОРОДА В КВАНОТОВОЙ МЕХАНИКЕ

1. Уравнение Шредингера для атома водорода

2. Решение радиальной части уравнения, квантование энергии атома

3. Решение угловой части уравнения, квантование орбитального момента импульса и проекции момента импульса электрона

4. Спин электрона, Опыты Штерна– Герлаха.

5. Принцип Паули, распределение электронов в многоэлектронных атомах. Таблица Менделеева.

12. ЗОННАЯ ТЕОРИЯ ТВЕРДОГО ТЕЛА

1. Образование энергетических зон в кристалле.

В свободных атомах электроны имеют совершенно одинаковый дискретный набор дозволенных уровней энергии. Но при объединении N ≈ 1023 атомов в кристалл электроны взаимодействуют не с одним, а со всеми атомами кристалла. В результате некоторый уровень энергии свободного атома в кристалле «расщепляется» на N уровней с ничтожно малой (10 –23 эВ) разностью энергий. Эти N уровней энергии образуют энергетическую зону. Каждый уровень энергии в зоне, согласно принципу Паули, могут занимать не более двух электронов.

Для объяснения электрических, тепловых, оптических свойств достаточно рассматривать две высшие зоны: валентную зону, образованную расщеплением основного уровня энергии валентных электронов, и зону проводимости, образованную расщеплением уровня энергии возбужденных электронов.

2. Деление твердых тел на проводники, полупроводники и

изоляторы

а). Проводники. Кристалл является проводником, если в валентной зоне есть свободные уровни энергии или она перекрывается с зоной проводимости. Под действием электрического поля электроны и дырки имеют право перемещаться в кристалле с увеличением скорости, занимая все более высокие уровни энергии.

Классическая электронная теория электропроводности предполагает, что в проводниках есть свободные электроны, которые ведут себя подобно идеальному газу. Количество свободных электронов примерно равно числу атомов. При включении электрического поля на тепловое движение накладывается дрейф – направленное движение под действием сил поля. Из-за рассеяния электронов на ионах в узлах кристаллической решетки происходит потеря кинетической энергии электронов с превращением в теплоту и возникает электрическое сопротивление. Электронная теория Друде−Лоренца подтверждает экспериментальные законы постоянного тока – закон Ома, закон Джоуля – Ленца. Но удельная проводимость σ оказывается на один-два порядка больше экспериментальных значений.

Объяснение дано в квантовой механике в зонной теории твердых тел. При температуре абсолютного нуля электроны заполняют попарно энергетические уровни, поднимаясь по уровням все выше. Наивысший занятый уровень энергии называется уровнем Ферми. Энергия Ферми ЕФ имеет значение 5–8 эВ. Это большая энергия, она соответствует энергии теплового движения при температуре более 10 000 К. Поэтому при нагреве (кТ<<ЕФ) распределение электронов по энергиям изменяется для малой доли, менее процента, вблизи уровня Ферми (рис. 1). Если валентная зона заполнена не полностью, либо перекрывается с зоной проводимости, то в этом случае электроны верхних уровней под действием электрического поля имеют право увеличивать кинетическую энергию, переходя на свободные уровни, перемещаться по кристаллу и переносить ток. Электроны из нижних уровней в электропроводности не участвуют. То есть в отличие от классической теории только малая часть валентных электронов переносит электрический ток.

б) Полупроводники. Полупроводники – это кристаллические тела, которые по электропроводности занимают промежуточное положение между металлическими проводниками и изоляторами. Но принципиальным отличием полупроводников от металлов является быстрое уменьшения сопротивления с ростом температуры, в то время как у металлов оно медленно растет. Также электропроводность полупроводников сильно зависит от примесей.

Полупроводники – это, как правило, кристаллы элементов 4-й группы таблицы Менделеева, например германия, кремния. При образовании кристалла между атомами возникает химическая связь четырех валентных электронов. При абсолютном нуле температуры все электроны связаны, и кристалл является изолятором. Но при комнатных температурах некоторые электроны, получив достаточную энергию теплового движения, могут оторваться от атома, стать свободными. Одновременно образуется вакантная, незаполненная связь, которую может занять какой-либо электрон из соседних атомов, оставив после себя вакантную связь, которую может занять следующий электрон. Прыжки большого числа электронов эквивалентны перемещению вакантной связи, обладающей положительным электрическим зарядом, так называемой «дырки». В электрическом поле электроны и дырки перемещаются в противоположных направлениях, создавая электрический ток. С ростом температуры число свободных электронов и дырок растет, что приводит к уменьшению сопротивления.

Кристалл является полупроводником, если валентная зона заполнена полностью, а зона проводимости отделена так называемой запрещенной зоной, ширина которой не более 2 электрон-вольт.

в. Изоляторы. Кристалл является изолятором, если валентная зона заполнена полностью, а зона проводимости отделена запрещенной зоной, ширина которой (условно) более 2 электрон-вольт. В этом случае энергии теплового движения электрона недостаточно для перехода электрона в зону проводимости. Свободных носителей заряда в изоляторах нет, зона проводимости пуста, электрическое сопротивление бесконечно.

4. Собственная проводимость полупроводников

При нуле абсолютной температуры ни тепловое движение, ни электрическое поле не в состоянии сообщить добавочную энергию электрону для перехода в зону проводимости и кристалл является изолятором. Но при комнатной температуре энергия теплового движения уже достаточна для ионизации атомов. Освободившиеся электроны переходят в зону проводимости и получают право перемещаться по кристаллу. Концентрация свободных электронов в зоне проводимости определяется распределением Больцмана

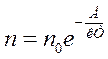. (1)

Здесь n0 – концентрация всех валентных электронов, Ε – ширина запрещенной зоны или энергия активации, кТ – мера энергии теплового движения электрона, равная произведению постоянной Больцмана на абсолютную температуру. Сопротивление кристалла обратно пропорционально концентрации электронов в зоне проводимости и дырок в валентной зоне, поэтому

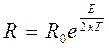. (2)

Здесь R0 – сопротивление полупроводника, если бы все валентные электроны стали свободными. Коэффициент «2» учитывает энергию активации, приходящуюся на два возникающих вместе заряда – на электрон и дырку. В чистом полупроводнике число свободных электронов равно числу дырок, они являются носителями заряда.

5. Примесная проводимость полупроводников

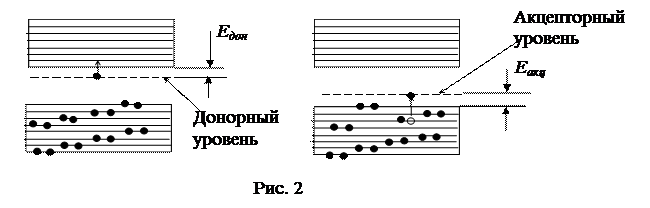
Влияние примесей в полупроводниках на электропроводность также объясняет зонная теория. Если, например, в кристалл 4-валентного полупроводника внести атом 5-валентной примеси, например фосфора, то один электрон окажется слабо связан с ядром атома. Его энергия будет чуть меньше, чем у свободных электронов и его энергетический уровень будет расположен близко ко дну зоны проводимости (рис. 2). Этот уровень энергии называется донорным. Энергия активации Едон для перехода электрона с донорного уровня в зону проводимости сравнительно мала. В кристалле, в зоне проводимости появляются электроны, они являются основными носителями электрического заряда. Это полупроводники n-типа.

Если в кристалл 4-валентного полупроводника внести атомы 3-валентной примеси, например индия, бора, то одна связь окажется незаполненной. Образуется дырка. Энергия электрона, занявшего дырку, немного больше, чем у других валентных электронов. Этот уровень энергии, называемый акцепторным, чуть выше потолка валентной зоны. Получив добавочную энергию Еакц,, на акцепторный уровень переходят электроны из валентной зоны, а в валентной зоне остается дырка. Дырки являются основными носителями заряда. Такие кристаллы называются полупроводниками p-типа (рис. 2).

Примесная составляющая сопротивления полупроводников определяется формулой

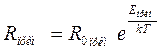. (3)

Полная электропроводность кристалла полупроводника складывается из собственной и примесной. При сравнительно низких температурах главную роль играет примесная проводимость, так как энергия активации примеси невелика. Но с ростом температуры, при почти полной ионизации сравнительно небольшого числа атомов примеси, рост концентрации электронов и дырок прекратится. Зато растет число электронов и дырок при ионизации собственных атомов кристалла. Собственная проводимость становится преобладающей при высоких температурах.

Если уравнения (2) и (3) прологарифмировать, то получим линейные уравнения для собственной и для примесной проводимости

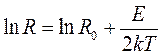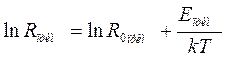, (4) . (5)

Логарифмы обоих видов сопротивлений линейно зависят от обратной температуры (рис. 3). Их угловые коэффициенты соответственно будут равны 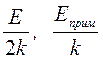. Таким образом, можно по графику определить энергию активации. Если она будет около электрон-вольта, то это собственный полупроводник, если доли электрон-вольта, то это примесный полупроводник.

13. КОНТАКТ ПОЛУПРОВОДНИКОВ С РАЗНЫМ ТИПОМ

ПРОВОДИМОСТИ

Электронно-дырочный переход, или p-n переход, – это область контакта двух полупроводников с различным типом проводимости: р-типа и n-типа.

Внесение ничтожных долей примеси в сверхчистый кристалл полупроводника изменяет тип проводимости. Полупроводник n-типа можно получить, если в кристалл 4-валентного, например германия, добавить небольшое количество 5-валентной примеси, например фосфора. Один валентный электрон атома примеси окажется слабо участвующим в химической связи. Его сравнительно легко оторвать от атома за счёт энергии теплового движения. Поэтому в полупроводниках n-типа электронов больше, чем дырок, и они являются основными носителями заряда, а дырки – неосновными носителями.

Полупроводник р-типа можно получить, если в кристалл 4-валентного сверхчистого полупроводника добавить небольшое количество трёхвалентной примеси, например индия. Одна химическая связь атома примеси оказывается незаполненной, то есть дыркой. При ионизации собственных атомов полупроводника также образуются дырки и электроны. Дырок в полупроводнике р-типа больше, чем электронов, и они являются основными носителями электрического заряда, а электроны – неосновными.

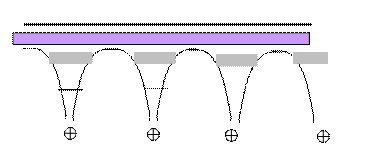
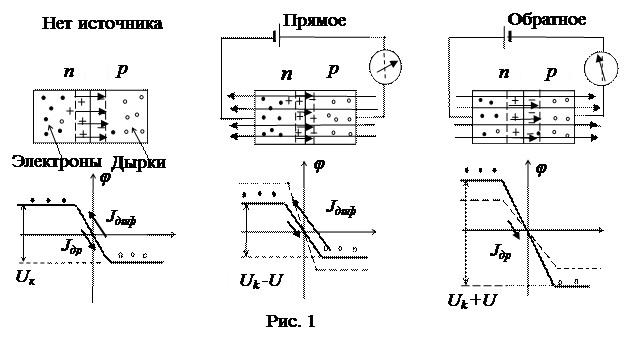
При образовании контакта полупроводников с разным типом проводимости, вследствие теплового движения электроны из n-полупроводника, где их много, диффундируют в р-полупроводник. Там они рекомбинируют, то есть заполняют вакантные связи, создавая отрицательно заряженный ион из атома примеси. И наоборот, дырки из р-полупроводника диффундируют в n-полупроводник, где они рекомбинируют с электронами с образованием положительного иона примеси. В результате около зоны контакта свободных зарядов ставится мало, а образовавшиеся в узлах кристаллической решетки ионы разного знака создают двойной электрический слой с так называемой контактной разностью потенциалов, Uк. Электрическое поле двойного электрического слоя препятствует дальнейшей диффузии основных носителей заряда. Для них возникает потенциальный барьер (рис.1). Его смогут преодолеть только те заряды, энергия теплового движения которых превышает барьер. Их концентрация, по уравнению Больцмана, растет с увеличением температуры: . Они создают ток диффузии

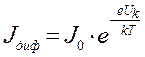. (1)

Здесь е – заряд электрона, k – постоянная Больцмана, Т – температура, J0 – сила тока, если бы все заряды переходили через барьер.

Зато контактное поле не препятствует, а, наоборот, увлекает неосновные носители заряда. Их движение создаёт ток дрейфа, противоположный току диффузии. В отсутствии внешних электрических полей устанавливается динамическое равновесие: ток дрейфа понижает барьер, а встречный ток диффузии его восстанавливает Jдр = Jдиф.

Электрическое поле, приложенное к электронно-дырочному переходу, нарушает равновесие. При прямом включении на кристалл р-типа подают положительный потенциал, а на кристалл n-типа – отрицательный (рис. 1, прямое). Внешнее поле при этом ослабляет контактное поле, понижает высоту потенциального барьера, и ток диффузии основных носителей возрастает. А ток дрейфа неосновных носителей остаётся постоянным. Результирующая сила тока определяется разностью тока диффузии и тока дрейфа:

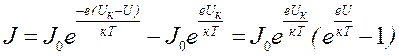. (2)

Коэффициент перед скобкой имеет смысл тока дрейфа. Поэтому формулу (2) можно переписать в виде

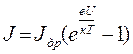. (3)

Если к электронно-дырочному переходу приложить обратное, запирающее напряжение, то внешнее поле усиливает контактное поле (рис. 1, обратное). Возрастает высота потенциального барьера. Ток диффузии основных носителей быстро падает практически до нуля. Остаётся постоянный по величине ток дрейфа, направленный от n-кристалла к р-кристаллу. Силу обратного электрического тока можно также определить по формуле (3), только полагая внешнее напряжение отрицательным.

Вольтамперная характеристика электронно-дырочного перехода, то есть зависимость силы тока от приложенного напряжения определяется теоретически уравнением (3). С ростом прямого напряжения результирующая сила тока растёт сначала медленно, пока внешнее напряжение не превысит контактное. Затем происходит быстрый рост силы тока, практически по экспоненциальному закону, так как током дрейфа (единицей в скобке уравнения 3) можно пренебречь. Таким образом, вольтамперная характеристика электронно-дырочного перехода является нелинейной: прямой ток большой, а обратный меньше в тысячи раз (рис. 2). Это свойство используется в полупроводниковых диодах для выпрямления переменного тока.

Дата добавления: 2014-01-04