Використання комплексних чисел для аналізу кіл синусоїдного струму

Застосування комплексних чисел для розрахунків кіл синусоїдного струму дає можливість замінити диференційні рівняння, якими описуються процеси у цих колах, алгебраїчними рівняннями. Метод аналізу та розрахунку електричних кіл синусоїдного струму з використанням комплексних часто називають символічним або комплексним методом.

З курсу математики відомо, що синусоїдну функцію, зокрема обертовий вектор-орт (рис. 2.10), можна записати комплексним числом. Тому при розрахунках електричних кіл синусоїдного струму, замість геометричних дій з векторами, використовують більш зручні і точніші алгебраїчні дії з комплексними числами.

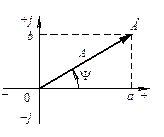
Відомо, що комплексне число може бути записано у алгебраїчній, показниковій і тригонометричній формах, відповідно:

; ; ,

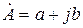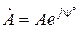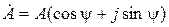де a та b – відповідно, дійсна та уявна складові комплексного числа (проекції вектора на вісі, відповідно, дійсних та уявних чисел); А – модуль комплексного числа (довжина вектора); y – аргумент комплексного числа (кут нахилу вектора до вісі дійсних чисел); 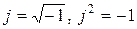– уявне число; е – основа натурального логарифму.

Для переходу від однієї форми запису комплексного числа до іншої використовують співвідношення (рис. 2.10):

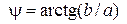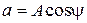;; та .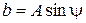

Комплекс діючого значення електричної величини, що змінюється у часі за синусоїдою, виділяють крапкою над символом, який відображає цю величину. Наприклад: 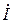– комплекс діючого значення струму; – комплекс діючого значення напруги. Якщо електрична величина не є синусоїдною, то комплекс її значення виділяють рискою під символом, який відображає цю величину. Наприклад: Z – комплекс повного опору; S – комплекс повної потужності.

Додавати або віднімати комплексні числа зручніше коли вони надані у алгебраїчній формі запису:

;

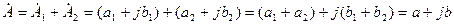Виконувати множення, або ділити – зручніше коли числа надані у показниковій формі:

;

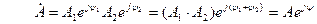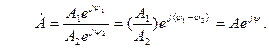
Комплекси величини, які відрізняються тільки за знаком аргументу, називають спряженими комплексами. В електротехніці спряжений комплекс звичайно виділяють “зірочкою” над символом величини. Так, наприклад, якщо маємо

,

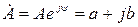то спряжений комплекс буде:

Зазначимо, що при множенні комплексу величини на спряжений комплекс, в результаті одержимо квадрат модуля цієї величини –

.

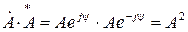Дата добавления: 2014-01-04