Коло синусоїдного струму з ємністю

Коло, яке стосовно джерела синусоїдної напруги u = U_Сm sin(w t + y _u) має виключно ємнісний характер навантаження можна надати у вигляді конденсатора ємністю С, що підключений до джерела дуже короткими провідниками (рис. 2.14, а).

Струм у такому колі являє собою рух зарядів q до обкладинок конденсатора і може бути описаний диференційним рівнянням –

де u_С – спад напруги на конденсаторі.

Враховуючи, що внутрішній опір з’єднувальних проводів дуже малий, і, отже, згідно з другим законом Кірхгофа –

,

рішення диференційного рівняння буде мати вигляд:

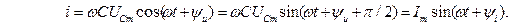
Розділивши обидві частини виразу амплітудного значення струму ємності (I_m = w CU_m) на 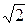, одержимо рівняння розрахунку діючого струму кола – закон Ома для кола (ділянки кола) з ємністю:

,

де x_C = 1/(w C) = 1/(2p fC) – реактивний опір ємності, або ємнісний опір, який відображає вплив ємності на величину діючого струму.

Для кола (ділянки кола) з ємністю закон Ома у комплексній формі буде:

З викладеного випливає, що струм у колі з ємністю, подібно до прикладеної напруги, змінюється за синусоїдним законом. Так як синусоїди напруги і струму кола з ємністю мають початкові фази, відповідно: y _u та y _i = y _u + p/2, то кут зсуву фаз між ними буде:

.

В загальному випадку суміщені часова та векторна діаграми струму і напруги кола (ділянки кола) з ємністю мають вигляд, як на рис. 2.14, б та рис. 2.14, в. При побудові цих діаграм прийнято, що y _u = 0^°.

Миттєву потужність кола з ємністю визначають так:

З аналізу рівняння розрахунку p випливає, що миттєва потужність кола (ділянки кола) з ємністю змінюється за синусоїдою частота якої у 2 рази більша, ніж у синусоїд струму або напруги.

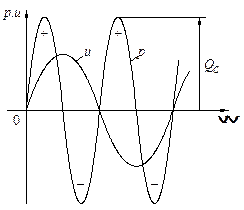
З графіка p = f (t) (рис. 2.15) видно, що протягом першої чверті періоду синусоїди напруги, ємність накопичує енергію (W_C = CU ² _Cm /2) з мережі (конденсатор заряджається) – іде процес перетворення енергії змінного струму в енергію електричного поля. У другу чверть періоду, ємність розряджається – віддає у мережу накопичену раніше енергію. Так відбувається безперервний періодичний процес обміну енергії між ємністю і мережею. Цей обмін відбувається без втрат енергії і тому середнє значення потужності кола (ділянки кола) з ємністю за період буде –

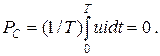
Потужність, яка без втрат коливається між джерелом і ємністю називають реактивною ємнісною потужністю Q_C, вар (вольт ампер реактивний). Її визначають за формулою:

,

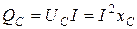Дата добавления: 2014-01-04