Равновесие потребителя

Вспомним, что спрос зависит от цен на товары и услуги, от дохода, от вкусов и предпочтений потребителя. Рассмотрим теперь, как предпочтения потребителя, выраженные через кривые безразличия, взаимодействуют с бюджетными ограничениями и каким образом осуществляется выбор оптимального сочетания товара Х и товара Y. На рис. 3,7 изображены линия бюджетного ограничения и карта предпочтений потребителя:

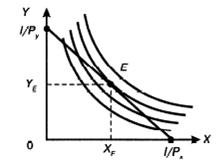
Рис. 3.7 Максимизация полезности потребителя при заданном бюджете

Потребитель желает выбрать такую комбинацию товаров X и У, которая обеспечит максимальную совокупную полезность и при этом позволит не выйти за пределы своего бюджета. Решая эту задачу графически, потребитель будет продвигаться по линии бюджетного ограничения от точки ее пересечения с горизонтальной осью вверх. При этом линия бюджетного ограничения будет поочередно пересекать кривые безразличия, обеспечивающие все более высокие уровни общей полезности. Такое движение будет осуществляться до тех пор, пока бюджетная линия не коснется наивысшей кривой безразличия, доступной для касания. В этой точке касания двух кривых (Е) достигается оптимальный выбор потребителя, при котором совокупная полезность в пределах данного бюджета максимизируется.

Если продвигаться далее вверх по бюджетной линии за пределами точки Е, бюджетная линия начнет пересекать поочередно кривые безразличия, обеспечивающие все более низкий уровень совокупной полезности, удаляя тем самым потребителя от искомой цели.

Таким образом, равновесие потребителя, или рациональный выбор потребителя, достигается в точке касания бюджетной линии с наивысшей доступной для касания кривой безразличия.

Рассмотрим иную ситуацию, когда стоит задача получить некоторую полезность при минимальных затратах (рис. 3.8).

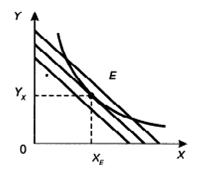
Рис. 3.8 Выбор потребителя при минимизации затрат

В точке касания (Е) кривой безразличия с наиболее низко расположенной бюджетной линией будет достигнута поставленная цель: данная комбинация двух благ обеспечивает искомую полезность и стоит менее всего.

Обратим внимание, что в точке касания наклоны двух кривых одинаковы. Наклон кривой безразличия равен предельной норме замещения. Наклон бюджетной линии равен отношению цены товара Х к цене товара У (с учетом минуса), или — Рх/Ру

Приравняв известные нам формулы наклона этих кривых, получим:

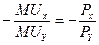
Разделив обе стороны неравенства на —Р_X и умножить на 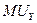можно вывести равнозначную, уже знакомую нам, формулу:

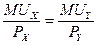
Таким образом, не прибегая к измерению полезности отдельного блага, при помощи кривых безразличия мы получили точно такой же вывод и аналогичную формулу, как и на основе использования теории предельной полезности.

Вопрос: Будет ли потребитель находиться в состоянии равновесия, если кривая безразличия пересекает бюджетную линию в двух точках?

Да, т.к. потребитель всегда находится в состоянии равновесия.

Да, т.к. условия пересечения кривых достаточно.

+Нет, т.к. равновесие достигается только в точке касания кривых.

Нет, т.к. равновесие потребителя - научная абстракция

Дата добавления: 2014-01-04