Л е к ц і я 2.8. Теплообмінні апарати. Тепломасообмін у двокомпонентних середовищах.

Поглинальна, відбивна та пропускна здатність тіл. Нехай зі всієї кількості енергії, що падає на тіло, частина поглинається, частина відбивається і частина проходить крізь тіло, так що. Якщо поділити обидві частини рівняння на, отримаємо або, де,, – поглинальна, відбивна і пропускна здатність тіла відповідно. Всі ці величини мають нульову розмірність і змінюються від 0 до 1.

Природа теплового випромінювання. Спектри випромінювання. Види променистих потоків. Поглинальна, відбивна та пропускна здатність тіл. Ефективне та результуюче випромінювання. Закони теплового випромінювання. Теплообмін випромінюванням між твердими тілами, що розділені прозорим середовищем. Теплообмін випромінюванням при наявності екранів. Особливості випромінювання газів.

Джерела інформації: [1], с.402-422; [2], с.229-241; [8], с.160-193.

Природа теплового випромінювання. Процеси променевого (радіаційного) теплообміну широко розповсюджені в теплотехніці, ядерній енергетиці, ракетній техніці, металургії, сушильній техніці, хімічній технології, геліотехніці і т.д.

Теплове випромінювання – процес розповсюдження внутрішньої енергії випромінюючого тіла шляхом електромагнітних хвиль. Електромагнітні хвилі це електромагнітні збурення, які виходять з випромінюючого тіла і розповсюджуються у вакуумі зі швидкістю світла с = 2,9979 ∙ 10⁹ м/с. При поглинанні електромагнітних хвиль іншим тілом вони знову перетворюються в енергію теплового руху молекул. Збудниками електромагнітних хвиль є заряджені матеріальні частинки, тобто електрони і іони, які входять до складу речовини. При цьому коливання іонів відповідають випромінюванню низької частоти; випромінювання, зумовлено рухом електронів, може мати високу частоту, якщо вони входять до складу атомів і молекул. Випромінювання металів, які мають вільні електрони, набуває характер імпульсів і має хвилі різної частоти, у тому числі хвилі низької частоти.

Крім хвильових властивостей випромінювання має також і корпускулярні властивості. Корпускулярні властивості полягають у тому, що променева енергія випромінюється і поглинається речовиною не безперервно, а окремими дискретними порціями – квантами світла або фотонами, енергія яких дорівнює 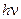, де 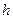= 6,62 ∙ 10^–34 Дж∙с – стала Планка, а 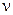– частота коливань еквівалентного магнітного поля. Фотон – частинка матерії, яка має енергію, кількість руху і електромагнітну масу. Тому теплове випромінювання можна розглядати як фотонний газ.

Для нас найбільший інтерес становлять ті промені, виникнення яких визначається тільки температурою і оптичними властивостями тіла. Такі властивості мають видимі або світлові та інфрачервоні або теплові промені з довжиною хвилі приблизно від 0,5 до 800 мкм. Ці промені називають тепловими, а процес їх розповсюдження – тепловим випромінюванням.

При попаданні на інші тіла енергія випромінювання частково поглинається ними, частково відбивається і частково проходить крізь тіло. Процес перетворення енергії випромінювання у внутрішню енергію поглинального тіла називають поглинанням.

Більшість твердих та рідких тіл випромінюють енергію всіх довжин хвиль в інтервалі від 0 до 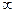, тобто мають суцільний спектр випромінювання. Гази і чисті не окислені речовини випромінюють енергію тільки у певних інтервалах довжин хвиль, тобто мають селективний спектр випромінювання. Тверді тіла випромінюють і поглинають енергію тонким поверхневим шаром (для непровідників теплоти він складає біля 1мм, для провідників теплоти – 1 мкм). Напівпрозорі тіла (плавлений кварц, скло, оптична кераміка і т.п.), а також гази і пара характеризуються об’ємним випромінюванням, в якому беруть участь всі частинки об’єму речовини.

Випромінювання тіл залежить від температури. Із збільшенням температури тіла його енергія випромінювання збільшується, бо збільшується внутрішня енергія тіла. При цьому змінюється і спектральний характер випромінювання. При збільшенні температури підвищується інтенсивність короткохвильового випромінювання. Залежність інтенсивності випромінювання від температури значно більша, ніж в процесах теплопровідності і конвекції. Тому при високих температурах основним видом переносу є теплове випромінювання.

Види променистих потоків. Розглянемо основні характеристики поверхневого (напівсферичного) випромінювання, при якому випромінювання розповсюджується під різними напрямками у межах напівсферичного тілесного кута. Кількість енергії випромінювання, що переноситься за одиницю часу через довільну поверхню, називається потоком випромінювання. Розрізняють монохроматичний потік випромінювання 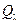(Вт/м), що відповідає вузькому інтервалу довжин хвиль, який можна характеризувати даним значенням довжини хвилі 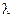, і інтегральний потік випромінювання 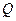(Вт), що відповідає усьому спектру випромінювання у межах від 0 до 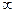. Потік випромінювання, що проходить через одиницю поверхні, називається поверхневою густиною потоку випромінювання. Поверхнева густина потоку інтегрального випромінювання , звідки 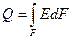. Якщо значення Е по всій поверхні однакове, то 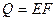. Поверхнева густина потоку монохроматичного випромінювання і пов’язана з густиною потоку інтегрального випромінювання співвідношенням , або .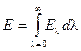

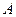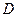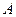Якщо тіло поглинає усі проміні, які падають на нього, тобто = 1, а = 0 і = 0, то воно називається абсолютно чорним. Властивістю абсолютно чорного тіла володіє отвір у стінці порожнистого тіла. Якщо вся промениста енергія, яка падає на тіло, відбивається, то = 1, а = 0 і 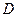= 0. Якщо при цьому відбивання підлягає законам геометричної оптики, то тіло називається дзеркальним. При дифузійному відбиванні, коли відбита промениста енергія розсіюється по всіх напрямках, тіло називається абсолютно білим. Якщо 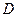= 1, а 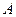= 0 і = 0, то тіло пропускає усі промені, які падають на нього, і називається абсолютно прозорим (або діатермічним).

У природі абсолютно чорних, білих та прозорих тіл не існує. Значення 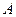, і 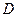залежать від природи тіла, його температури і спектра падаючого випромінювання. Наприклад, повітря для теплових променів прозоре, але при наявності у ньому водяної пари або вуглекислоти воно стає напівпрозорим. Тверді тіла і деякі рідини (вода, спирт) для теплових променів практично непрозорі, тобто 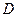= 0. В цьому випадку A + R = 1. З цього співвідношення витікає, якщо тіло добре відбиває променеву енергію, то воно погано поглинає, і навпаки.

Поряд з цим є тіла, які прозорі тільки для деяких довжин хвиль. Наприклад, віконне скло прозоре тільки для світлових променів, а для ультрафіолетових воно майже непрозоре. Теж відноситься і до поняття поглинання і відбивання. Біла за кольором поверхня добре відбиває лише світлові промені (це використовується на практиці, наприклад, біле фарбування поверхонь, де інсоляція небажана). Невидимі (інфрачервоні) теплові промені біла поверхня поглинає так добре, як і темна.

Для поглинання і відбивання теплових променів більше значення має не колір, а стан поверхні. Незалежно від кольору відбивна здатність гладких і полірованих поверхонь у багато разів вище, ніж шорстких. Для збільшення поглинальної здатності тіл їх поверхню покривають темною шорсткою фарбою, наприклад, нафтовою сажею, для якої 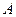= 0,90 … 0,96.

Ефективне та результуюче випромінювання. Якщо на тіло ззовні не падають ніякі промені, то з одиниці поверхні тіла відводиться променистий потік енергії, який повністю визначається його температурою та фізичними властивостями. Це власне випромінювання тіла 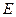, Вт/м², (рис. 8.1). Промениста енергія, яка падає з боку інших тіл на тіло, яке розглядається, це падаюче випромінювання 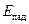. Частина падаючого випромінювання в кількості 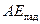поглинається тілом – поглинуте випромінювання 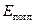; інше у кількості відбивається – відбите випромінювання 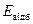. Власне випромінювання тіла в сумі з відбитим називається ефективним випромінюванням

. (8.1)

Це фактичне випромінювання тіла, яке ми вимірюємо приладами і відчуваємо. Воно залежить від фізичних властивостей і температури не тільки даного випромінюючого тіла, але й інших оточуючих його тіл, а також від форми, розмірів і відносного розташування тіл у просторі.

Рис. 8.1. До складання балансу променистої енергії

Різниця між власним випромінюванням тіла і тією частиною падаючого зовнішнього випромінювання, яке поглинається даним тілом, називається результуючим випромінюванням . Складемо рівняння балансу енергії, що проходить крізь площини а-а і б-б, одна з яких розташована усередині, а інша – зовні цього тіла поблизу його поверхні (див. рис. 8.1) Для площини а-а

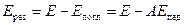; (8.2)

для площини б-б

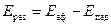. (8.3)

Величина визначає потік енергії, який дане тіло передає оточуючим його тілам у процесі променистого випромінювання. Якщо має від’ємний знак (< 0), це означає, що тіло внаслідок променистого теплообміну отримує енергію. Якщо > 0, навпаки, віддає енергію.

Визначимо залежність між ефективним, результуючим і власним випромінюванням. З (8.3) маємо

, (8.4)

а з (8.2)

. (8.5)

Якщо підставити останній вираз в рівняння (8.4), отримаємо

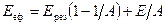. (8.6)

Це рівняння широко використовується при розрахунках променистого теплообміну між тілами.

Закони теплового випромінювання. Закон Планка. Цей закон встановлює залежність поверхневої густини потоку монохроматичного випромінювання абсолютно чорного тіла від довжини хвилі і температури (індекс 0 означає, що величина відноситься до абсолютно чорного тіла)

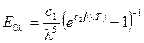, (8.7)

де 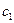= 3,74 ∙ 10^-16 Вт ∙ м²; = 1,44 ∙ 10^-2м ∙ К; 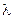– довжина хвилі випромінювання; Т – абсолютна температура тіла, К.

З рис. 8.2 видно, що при будь-яких температурах при 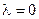і 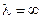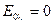, а при деякому проміжному значенні спостерігається максимум густини потоку випромінювання. Для усіх довжин хвиль тим більше, чим вище температура. З підвищенням температури максимум кривих зміщується в бік більш коротких хвиль. Зв’язок між і встановлюється законом Віна: = 2,9 ∙ 10^{-3, м ∙ К. На рис. 8.2 площа під кривою – повна кількість променистої енергії, що випромінюється всіма довжинами хвиль .}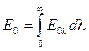

Рис. 8.2. До розгляду закону Планка

Для реальних тіл залежність густини потоку випромінювання від 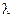і може бути установлена тільки на основі дослідного вивчення їх спектра. При цьому, якщо спектр випромінювання безперервний і крива подібна до відповідної кривої для абсолютно чорного тіла з тією ж температурою, тобто якщо для всіх довжин хвиль = const, то таке випромінювання називається сірим, а тіла з таким випромінюванням – сірими. Дослід показує, що випромінювання багатьох технічних матеріалів практично можна розглядати як сіре.

Спектри випромінювання реальних тіл 3, абсолютно чорного тіла 1 і сірого 2 показані на рис. 8.3. для реальних (і сірих) тіл на будь-якій довжині хвилі ніколи не перевищує . У випадку селективного випромінювання на деяких ділянках довжин хвиль = 0.

Закон Стефана – Больцмана. Ступінь чорноти. Закон встановлює залежність густини потоку інтегрального випромінювання абсолютно чорного тіла 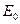від температури. Якщо зінтегрувати рівняння Планка (8.7) по всіх довжинах хвиль від 0 до 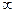, отримаємо для абсолютно чорного тіла:

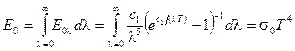, (8.8)

де 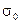– стала Стефана – Больцмана, вона дорівнює 5,67∙10^-8 Вт / (м² ∙ К⁴). Це рівняння носить назву закону Стефана – Больцмана. У технічних розрахунках цей закон використовується у більш зручній формі:

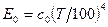, (8.9)

де 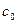– коефіцієнт випромінювання абсолютного чорного тіла; 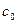= 5,67 Вт / (м² ∙ К⁴).

Рис. 8.3. Спектри випромінювання різних тіл

Дослідами показано, що цей закон може бути застосований і до реальних (сірих) тіл. У цьому випадку він приймає вигляд:

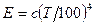, (8.10)

де – коефіцієнт випромінювання сірого тіла.

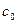Для різних тіл коефіцієнт випромінювання різний. Його значення визначається природою тіла, станом поверхні і температурою; завжди менше за і може змінюватися від 0 до 5,67. Відношення густини потоку власного випромінювання тіла до густини потоку випромінювання абсолютно чорного тіла з тією ж температурою називається ступенем чорноти :

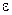. (8.11)

Значення 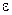змінюється від 0 до 1. Для технічно важливих матеріалів значення 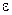приводять в таблицях. У цьому випадку рівняння (8.10) приймає вид

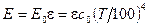. (8.12)

Більш детальною характеристикою тіла є спектральний ступінь чорноти :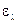

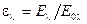. (8.13)

При фіксованій температурі величина 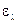в загальному випадку залежить від довжини хвилі 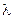і може змінюватися від 0 до 1. Для сірого тіла при фіксованій температурі 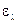= const.

Ступінь чорноти залежить від природи тіла, його температури, стану поверхні. Для матеріалів із збільшенням температури вона зростає. При шорсткості поверхні, її забрудненні або окисненні 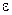може збільшуватися у декілька разів. Наприклад, для полірованого алюмінію 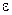= 0,04 … 0,06, при окисненні поверхні 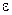= 0,2 … 0,3.

Закон Кірхгофа. Установлює зв’язок між власним випромінюванням тіла та його поглинальною здатністю. Розглянемо дві паралельні поверхні, одна з яких є абсолютно чорною з температурою , інша – сіра з температурою і поглинальною здатністю 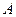. Відстань між поверхнями настільки мала, що промені, які випромінюються однією поверхнею, обов’язково попадуть на протилежну. Сіра стінка випромінює енергію 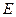і поглинає частину випромінювання чорного тіла 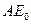. Енергія 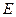і відбита сірим тілом енергія 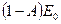попадають на чорне тіло і поглинаються їм. Результуюча густина потоку випромінювання сірого тіла 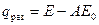. Якщ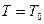о , то 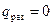, так що

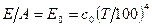. (8.14)

Отже, відношення власного випромінювання до поглинальної здатності при тепловій рівновазі для всіх тіл однакове і дорівнює власному випромінюванню абсолютно чорного тіла з тією ж температурою. У цьому полягає сутність закону Кірхгофа, який дійсний і для монохроматичного випромінювання 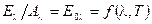. Відношення власного випромінювання визначеної довжини хвилі до поглинальної здатності при тій же довжині хвилі для всіх тіл одне й теж і є функцією тільки довжини хвилі і температури. Тут – поглинальна здатність у вузькому інтервалі довжин хвиль.

З рівняння (8.14) 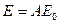, а (8.10) – 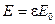. Таким чином, з закону Кірхгофа також витікає, що при тепловій рівновазі поглинальна здатність сірих тіл чисельно дорівнює ступеню чорноти тіла, тобто 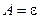, а також 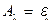. Отже, власне випромінювання тіл тим більше, чим більше їх поглинальна здатність. Тому тіла, які добре відбивають променисту енергію, самі випромінюють дуже мало. Крім того, тіло, яке випромінює енергію на визначеній довжині хвилі, має здатність поглинати її на тій же довжині хвилі.

Закон Ламберта. Зміна енергії випромінювання за окремими напрямками визначається законом Ламберта. Кількість енергії, яка випромінюється у напрямку (рис. 8.4) за одиницю часу з одиниці поверхні тіла у межах одиничного тілесного кута, називають кутовою густиною випромінювання:

. (8.15)

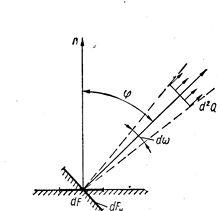
Рис. 8.4. До розгляду закону Ламберта

Іншою характеристикою спрямованого випромінювання є яскравість (інтенсивність) випромінювання, тобто кількість енергії, яка випромінюється в напрямку за одиницю часу і віднесена до одиниці тілесного кута і одиниці поверхні, що ортогональна до напрямку випромінювання (див. рис. 8.4):

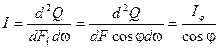. (8.16)

Згідно закону Ламберта потік випромінювання 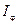абсолютно чорного тіла у напрямку пропорційний потоку випромінювання 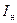у напрямку нормалі до поверхні і косинусу кута між ними, тобто

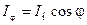. (8.17)

Отже, найбільша кількість енергії поверхнею випромінюється у напрямку нормалі при = 0; із збільшенням кількість енергії зменшується і при = 90^о вона стає рівною нулю.

З (8.16) і (8.17) знаходимо 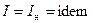. Отже, якщо випромінювання підкоряється закону Ламберта, то яскравість не залежить від напрямку. Величину можна виразити через густину інтегрального випромінювання 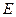, якщо взяти інтеграл у межах півсфери:

.

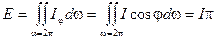Звідки і вираз закону Ламберта буде мати вид .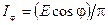

Закон Ламберта строго виконується лише для абсолютно чорного тіла. Для шорстких тіл цей закон підтверджується дослідом лише для 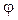= 0 … 60^о. Більш різке відхилення від закону Ламберта спостерігається для полірованих металів.

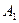Теплообмін випромінюванням між твердими тілами, що розділені прозорим середовищем. Розглянемо стаціонарний променистий теплообмін в замкненій системі, яка складається з двох сірих тіл (рис. 8.5, а). Площа поверхні першого тіла , другого – ; відповідні значення поглинальної здатності тіл – і 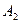, температур – і 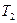; при цьому > .

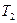Рис. 8.5. До розгляду променистого теплообміну між тілами

Частка повного променистого потоку одного тіла, що попадає на друге тіло, називається кутовим коефіцієнтом випромінювання φ:

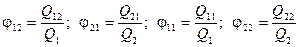. (8.18)

Тут 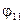і 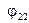ураховують частку променистої енергії, що замикається на випромінюючому тілі; для плоскої і випуклої поверхонь 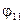і 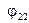дорівнюють нулю.

Розглянемо деякі властивості кутових коефіцієнтів. При однакових температурах двох абсолютно чорних тіл, що беруть участь у променистому теплообміні:

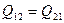. (8.19)

У загальному випадку потік енергії, що випромінюється тілом, дорівнює 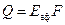. Для абсолютно чорного тіла ефективне випромінювання дорівнює власному і при заданих температурних умовах 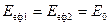. З урахуванням (8.18) і (8.19)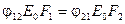. Звідки

, (8.20)

де 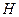– взаємна поверхня випромінювання.

Властивість кутових коефіцієнтів, що виражається рівнянням (8.20), називається властивістю взаємності. Для системи з n тіл:

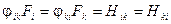, (8.21)

де індекси і і k віднесені до двох пар довільних поверхонь 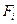і 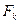, що беруть участь у теплообміні.

Згідно закону збереження енергії потоки випромінювання будь-якого тіла, що попадають на всі інші тіла системи, дорівнюють потоку власного випромінювання цього тіла:

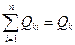, або ,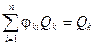

отже

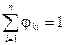, (8.22)

Ця властивість кутових коефіцієнтів називається властивістю замикаємості. Для замкненої системи з двох тіл ця властивість записується у виді

.

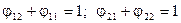Є багато аналітичних виразів, що дають змогу розрахувати кутові коефіцієнти для складних систем. Рівняння (8.21) і (8.22) дають змогу знайти значення у випадку простих систем. Для двох паралельних нескінченних поверхонь (рис. 8.5, б) 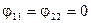. Тоді з (8.22) 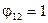і 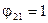. Якщо одна з поверхонь, що бере участь у теплообміні, не вгнута (рис. 8.5, в, г), то 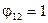і з рівняння (8.20) отримаємо .

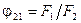Для системи з двох сірих тіл (рис. 8.5, а) результуючий тепловий потік від першого тіла до другого

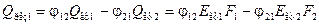. (8.23)

На основі рівняння (8.6) маємо

;

.

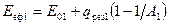Якщо підставити значення 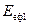і 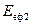в рівняння (8.23), отримаємо

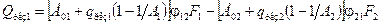
або

. (8.24)

При усталеному режимі результуючі теплові потоки для обох тіл однакові і протилежні за знаком (= –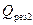), так що (8.24) приймає вид

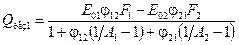
або

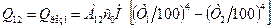, (8.25)

де

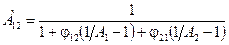, (8.26)

– приведена поглинальна здатність замкненої системи з двох сірих тіл.

Вираз (8.25) є загальний розв’язок задачі теплообміну двох сірих тіл і має велике практичне значення. Застосуємо його для ряду часткових випадків.

Для двох паралельних необмежених поверхонь (рис. 8.5, б) 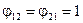і 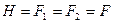. Отже з (8.25) і (8.26) маємо

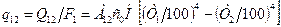(8.27)

і

.

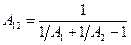Якщо перше тіло не має угнутості і все його ефективне випромінювання повністю падає на друге тіло (див. рис. 8.5, в, г), то 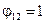,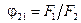і 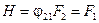. З урахуванням цього

(8.28)

і

.

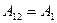Коли тіло випромінює у необмежений простір, то >> і з (8.28) витікає, що , тобто приведена поглинальна здатність визначається поглинальною здатністю меншого тіла.

Теплообмін випромінюванням при наявності екранів. Найбільш ефективним засобом теплоізоляції високотемпературних поверхонь є установлення екранів. Покажемо це на прикладі двох плоских паралельних поверхонь, між якими розміщено екран у вигляді тонкої пластини. Приймемо для простоти, що поглинальні здатності обох поверхонь однакові, тобто 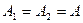, а поглинальна здатність екрана дорівнює 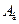. Температури поверхонь відповідно дорівнюють 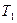і .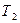

Тепловий потік від першої поверхні до другої без екрана:

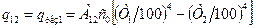, (8.29)

де

.

Запишемо рівняння для результуючих потоків між першою поверхнею і екраном 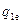, а також між екраном і другою поверхнею , вважаючи, що внутрішній термічний опір екрана 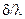малий і температура на обох його поверхнях однакова і дорівнює :

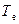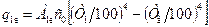; (8.30)

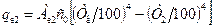, (8.31)

де

; ,

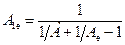тобто = .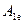

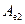При усталеному режимі 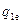= = 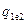, де – результуючий тепловий потік між поверхнями при наявності екрана.

Розв’язавши рівняння (8.30) і (8.31) відносно різниці температур і склавши отримані рівняння, знайдемо:

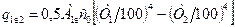. (8.32)

Якщо поділити (8.29) на (8.32), визначимо, у скільки разів екран послаблює тепловий потік між поверхнями:

.

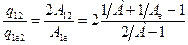З останнього виразу витікає, що ослаблення теплового потоку тим більше, чим менше поглинальна здатність екрана 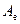. Якщо , то = 0,5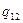. Значне зменшення теплового потоку досягається при установленні n екранів. У випадку плоских поверхонь з n екранами результуючий тепловий потік визначається за формулою (8.27), у якій

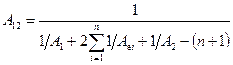, (8.33)

де 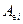– поглинальна здатність і -го крана.

Особливості випромінювання газів. Одно- і двоатомні гази практично прозорі для теплового випромінювання. Значну випромінювальну і поглинальну здатність мають три- і багатоатомні гази. До таких газів відносяться СО₂ і Н₂О, які вміщуються у продуктах згоряння органічного палива. На відміну від твердих і рідких тіл випромінювання газів носить об’ємний характер, бо в ньому беруть участь усі мікрочастинки газу. Тому їх випромінювальна і поглинальна здатність залежить від густини і товщини газового шару. Гази випромінюють і поглинають енергію тільки у визначених інтервалах довжин хвиль, які називають смугами спектра. У іншій частині спектру вони є прозорими. Отже випромінювання і поглинання газів носить вибірковий (селективний) характер. Так для СО₂ і Н₂О можна виділити по три основні смуги поглинання:

	СО2	Н2О
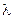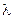, мкм	, мкм
2,4 … 3,0 4, 0 … 4,8 12,5 … 16,5	2,2 … 3,0 4,8 … 8,5 12 … 30

Смуги поглинання СО₂ частково співпадають зі смугами поглинання Н₂О. Спектральні смуги поглинання Н₂О більш широкі. Внаслідок цього коефіцієнти поглинання і випромінювання Н₂О суттєво більше, ніж СО₂.

Кількість енергії, яка поглинається газом, залежить від кількості молекул, що знаходяться у даному об’ємі газу. Кількість молекул пропорційна товщині газового шару, яка характеризується довжиною шляху променя 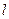, парціальному тиску газу 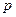та його температурі . Отже,

.

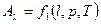У відповідності до закону Кірхгофа

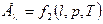. (8.34)

Для кожної і -ї смуги спектра

.

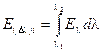Поверхнева густина теплового потоку інтегрального випромінювання газового середовища визначається сумою значень для окремих смуг, тобто

.

Експериментальні дані показують, що випромінювання газів не відповідає залежності від термодинамічної температури у четвертому степені. Однак у практичних розрахунках користуються законом четвертого степеня, уводячи відповідну поправку до значення ступеня чорноти газу:

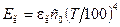, (8.35)

де 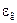– ступінь чорноти газового шару, який залежить від температури, тиску і товщини шару газу. Значення 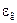для СО₂ і Н₂О наведені у літературі у виді номограм.

Ступінь чорноти газових сумішей визначається як сума ступенів чорноти окремих компонентів. Густина променистого потоку, який передається від газу до оточуючих стінок, можна розрахувати за формулою

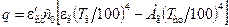, (8.36)

де 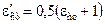– ефективний ступінь чорноти стінок каналу; 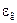– ступінь чорноти газів при їх середній температур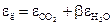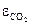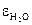і: ; , і 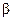визначають з номограм [1,2]; 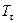– середня температура газів, К; 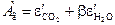– поглинальна здатність газу при середній температурі стінок каналу; визначається за тими ж номограмами; 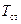– середня температура стінок каналу, К.

Наближене значення середньої довжини шляху променя визначається виразом

,

де – об’єм газу, 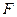– площа поверхні стінок каналу.

Дата добавления: 2014-01-04