Теплоотдача при свободной конвекции

Свободная, или естественная, конвекция возникает в связи с изменением плотности

жидкости от нагревания, которое происходит неравномерно. Свободная конвекция имеет

-место у нагретых стен печей, трубопроводов, у радиаторов центрального отопления, в

холодильниках при охлаждении продуктов и в других случаях. Этот вид теплообмена играет большую роль как в промышленности, так и в быту. Свободный теплообмен возникает в ■неравномерно нагретом газе или жидкости, находящихся как в ограниченном, так и в

-члеограниченном пространстве. Если тело имеет более высокую температуру, чем окружающая среда, то слои жидкости, нагреваясь от тела, становятся легче и под действием "юзникающей подъемной силы поднимаются вверх, а на их место поступают из

-^окружающего пространства более холодные слои. Поэтому и возникает свободное движение (рис. 2.34).

\

\ Г

N

у/

я

о ^

о

#;₍

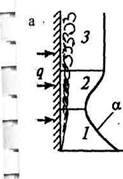
Рис. 2.34. Характер движения жидкости при естественной конвекции в неограниченном

пространстве:? при нагреве вертикальной стенки (а); при нагреве горизонтальной стенки сверху (б); при нагреве _ горизонтальной стенки снизу (в); при нагреве горизонтальной трубы изнутри (г); 1,2 и 3 -соответственно ламинарный, переходный и турбулентный участки движения жидкости

^4

Аналитические решения задач по определению теплоотдачи при свободном ламинарном и турбулентном движениях выполнены при целом ряде упрощающих допущений, поэтому эти решения большого практического применения не получили. Все наши знания по определению коэффициента теплоотдачи в основном базируются на эксперименте.

Глубокие экспериментальные исследования по теплоотдаче в свободном потоке были выполнены академиками М. В. Кирпичевым, М. А. Михеевым и их учениками. Многочисленные исследования по теплоотдаче в свободном потоке жидкости были проведены с горизонтальными и вертикальными проволоками, трубами, плитами и шарами. Опыты проводились с воздухом, водородом, углекислым газом, водой, маслом и различными органическими жидкостями. В результате обобщения опытных данных были получены эмпирические уравнения подобия.

Рассмотрим свободный теплообмен в неограниченном пространстве у вертикальной плиты или трубы (рис. 2.34 а). Возникающее свободное движение жидкости у вертикальных поверхностей может быть как ламинарным, так и турбулентным. Характер движения жидкости в основном зависит от температурного напора Аг = 1_ст - (_ж (здесь 1_Ш - температура нагретой поверхности; 1_Ж - температура неподвижной жидкости вдали от поверхности). При малых значениях температурного напора вдоль всей поверхности наблюдается ламинарное движение жидкости. При больших температурных напорах преобладает турбулентный режим движения. В развитии свободного движения форма тела играет второстепенную роль. Основное значение для свободного движения жидкости имеет длина поверхности, вдоль которой происходит теплообмен.

Характерная картина свободного движения и изменение коэффициента теплоотдачи вдоль вертикальной стенки показаны на рис. 2.34 а. У нижней части стенки в поднимающемся с небольшой скоростью воздухе (жидкости) наблюдается ламинарное движение с постепенно увеличивающейся толщиной ламинарного пограничного слоя. На некотором расстоянии от нижнего конца стенки по ее высоте ламинарный пограничный слой начинает разрушаться, возникает локонообразное движение жидкости, которое постепенно усиливается и переходит в развитое турбулентное движение с ламинарным подслоем в непосредственной близости к поверхности. В соответствии с изменением толщины пограничного слоя и характера движения жидкости у поверхности изменяется и коэффициент теплоотдачи. По мере увеличения ламинарного пограничного слоя, считая от нижнего конца стенки, коэффициент теплоотдачи уменьшается. Минимального значения коэффициент теплоотдачи достигает там, где толщина ламинарного пограничного слоя будет максимальной. В области переходного движения коэффициент теплоотдачи постепенно возрастает и принимает наибольшее постоянное значение в области развитого турбулентного движения жидкости. На рис. 2.34 а показана зависимость коэффициента а только от высоты стенки. Переменность физических параметров жидкости и температурного напора по высоте может привести к изменению коэффициентов теплоотдачи. В среднем теплоотдача при переходном режиме возрастает от значения, соответствующего ламинарному течению, до значения, соответствующего турбулентному движению жидкости.

Для определения среднего коэффициента теплоотдачи при свободном ламинарном движении жидкости вдоль вертикальных стенок и труб, если (Ог_жгРг_ж) < 10³ •*- 10⁹, то можно использовать следующее уравнение:

Ки_ж1=0,75(Ог_жГРг_ж)⁰<²⁵(Рг_ж/Рг_ст)°>²⁵. ".'-.:, (2.123)

Для определения среднего коэффициента теплоотдачи при свободном турбулентном движении жидкости вдоль вертикальной стенки, которое наступает при произведении чисел (Ог_Ж1-Рг_ж) > 6 ■ 10¹⁰, предложена следующая формула

№_ж1 = 0,\5(Ог_ж1 ■ Рг_ж)**\Рг_ж/Рг_ст)°>²⁵. (2.124)

Уравнения (2.123), (2.124) получены для чисел Рг_ж > 0,7. В этих формулах за -п ^грпределяющую температуру принята температура жидкости вдали от нагретой поверхности; за определяющий размер - длина поверхности, отсчитываемая от начала теплообмена.

На рис. 2.34 (б-г) показан характер свободного движения жидкости около горячих

— п горизонтальных поверхностей и труб. Особенностью свободного движения жидкости около

горизонтальных труб является то, что у труб малого диаметра восходящий поток сохраняет

"ламинарный режим даже вдали от трубы, а при большом диаметре переход в турбулентный

■"• режим может происходить в пределах поверхности самой трубы.

Для определения средних коэффициентов теплоотдачи при свободном ламинарном движении жидкости около горизонтальных труб при 10³ < {Ог^Рг^ < 10⁸ может быть "" применена формула

~ч

ч0,25

0,25/

Ш_жй = 0,5(Ог_жа ■Рг_ж)^{Рг_ж/Рг_ст)

(2.125)

Здесь за определяющую температуру принята температура капельной жидкости или

1 газа вдали от трубы, а за определяющий размер - наружный диаметр трубы.

-щ В теплотехнике встречаются случаи, когда свободная конвекция возникает в

ограниченном пространстве (рис. 2.35). Теплоотдача в замкнутом ограниченном

1 пространстве не может развиваться свободно, поэтому условия теплообмена в этом случае

-п определяются формой и размерами пространства. Рассчитать такой теплообмен достаточно

трудно. Для упрощения расчета сложный процесс теплообмена заменяют

"теплопроводностью путем введения понятия эквивалентного коэффициента

т теплопроводности, Х_экв, Вт/(м-°С)

"I

2 = ^Лэкв

дЗ

А1

(2.126)

-где д - плотность теплового потока, Вт/м; 3 - толщина (ширина) замкнутого пространства,
^м; Лг - разность температур между параллельными поверхностями замкнутого
пространства, °С.,,,

и>и

шшшю и

К л Ч д

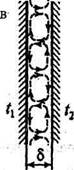
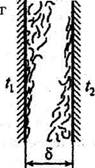
Рис. 2.35. Характер естественного движения жидкости, находящейся в ограниченном

пространстве: горизонтальная прослойка при нагреве сверху (а); горизонтальная прослойка при

нагреве снизу (б); вертикальные прослойки разной ширины (в, г)

Влияние конвекции учитывается с помощью коэффициента конвекции е_к, Представляющего собой отношение Х_экв к 1 той же среды при средней температуре. 3 приближенных расчетах при (Ог^-Рг^ > 10³ принимают

^: е_к=0,1Я-(вг_ж6Рг_ж)°>²⁵ После определения е_к вычисляют Х_экв и д по формулам

(2.127)

Аэкв -^ек* '

(2.128)

Ч = к_ш*. (2.129)

В уравнении (2.127) при определении чисел подобия (независимо от формы прослойки) за определяющий размер принята ее толщина б, а за Определяющую температуру - средняя температура (_ср= 0,5(/^>]+ (г)-

Дата добавления: 2014-01-04